德州市2005-2006学年度高二年级期末考试
高二数学(理)
一、选择题
1.![]() =( )A.
=( )A.![]() B.
B.![]() C.
2 D.-2
C.
2 D.-2
2.在抛物线y2=2px(p>0)上,横坐标为4的点到焦点的距离是5,则p的值为( )
A.![]() B.1 C.2 D.4
B.1 C.2 D.4
3.中心在坐标原点,离心率为![]() 的双曲线焦点在y轴上,则它的渐近线方程为( )
的双曲线焦点在y轴上,则它的渐近线方程为( )
A.y=![]() x B.y=
x B.y=![]() x
C.y=
x
C.y=![]() x
D.y=
x
D.y=![]() x
x
4.椭圆![]() 的内接正方形的面积是( )
的内接正方形的面积是( )
A.![]() B.12 C.24 D.48
B.12 C.24 D.48
5.用数学归纳法证明![]() (n是正整数)时,当n由k到k+1,不等式左边的变化是( )
(n是正整数)时,当n由k到k+1,不等式左边的变化是( )
A.增加![]() 一项
B.增加
一项
B.增加![]() 和
和![]() 两项且减少
两项且减少![]() 一项
一项
C增加![]() 和
和![]() 两项D.增加
两项D.增加![]() 一项
一项
6. 空间四边形OABC中,![]() 点M在OA上,且
点M在OA上,且![]() =2
=2![]() ,N为BC的中点,则
,N为BC的中点,则![]() 等于()
等于()
A.![]()
![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.己知双曲线的两个焦点为![]()
![]() ,
,![]()
![]() ,p是此双曲线上一点且
,p是此双曲线上一点且![]()
![]()
![]() 则该双曲线的方程为( )
则该双曲线的方程为( )
A.![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
8.己知F1,F2分别为椭圆![]() 的左右焦点,M为椭圆上的一点,MF1垂直于x轴,且∠F1MF2=60°,则椭圆的离心率为( )
的左右焦点,M为椭圆上的一点,MF1垂直于x轴,且∠F1MF2=60°,则椭圆的离心率为( )
A.![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
![]()
9. ![]() 的最小值是()
的最小值是()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.空间不共面的四点O、A、B、C,若![]() =0,且OA=OB=OC,则<
=0,且OA=OB=OC,则<![]() >=( )
>=( )
A.450 B.600 C.900 D.1350
11. 在正方体ABCD-A1B1C1D1中,点p是侧面BB1C1C内一动点,若点p到直线
BC与直线C1D1的距离相等,则动点p的轨迹是( )
A.双曲线 B.圆 C.椭圆 D.抛物线
12.在以下命题中,不正确的个数为( )
①![]() 共线的充要条件。②若
共线的充要条件。②若![]() ,则存在惟一的实数
,则存在惟一的实数![]() 使
使![]() ③对空间任意一点O和不共线三点A,B,C若
③对空间任意一点O和不共线三点A,B,C若![]() ,则P、A、B、C四点共面。
,则P、A、B、C四点共面。
![]()
![]() ④若
④若 ![]() 为空间的一个基底,则
为空间的一个基底,则 ![]() 构成空间的另一个基底
构成空间的另一个基底
A.1 B.2 C.3 D.4
二、填空题
13. 己知![]()
![]() 且
且![]() 则x=
则x=
14. 直线x-y+1=0和椭圆![]() 相交于A、B两点,则弦
相交于A、B两点,则弦![]()
15. 把正方形ABCD沿对角线AC折成直二面角,点E、F分别为AD、BC的中点,点O为原正方形ABCD的中心,则折起后∠EOF= .
16.设x1,x2 ![]() R常数a>0,定义运算
R常数a>0,定义运算![]() ,等号右边是通常的乘法运算,如果在平面直角坐标系中,动点p的坐标(x,y)满足关系式:
,等号右边是通常的乘法运算,如果在平面直角坐标系中,动点p的坐标(x,y)满足关系式:![]() ,则动点p的轨迹方程是
,则动点p的轨迹方程是
17.已知f(z)=1+![]() -
-![]() ,且f(-
,且f(-![]() )=10+3i,求复数
)=10+3i,求复数![]() .
.
18.棱长为1的正方体ABCD-A1B1C1D1,E,F,G分别是DD1、BD、BB1的中点
(1) 求证:EF![]() CF。(2)求EF与CG所成角的余弦值。
CF。(2)求EF与CG所成角的余弦值。
19.若一直线与抛物线y2=2px(p>0)交于A,B两点,且![]() ⊥
⊥![]() ,坐标原点O在直线AB的射影为D(2,1),求该抛物线的方程.
,坐标原点O在直线AB的射影为D(2,1),求该抛物线的方程.
20.是否存在实数a、b使等式22+42+62+…+(2n)2=n(n+1)(an+b)对任意的正整数n都成立,若不存在,说明理由;若存在,试确定a,b的值,并用数学归纳法证明之.
21.直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F是CE上的点,且BF![]() 平面ACE
平面ACE
(1)求证:AE![]() 平面BCE(2)求二面角B-AC-E的大小(3)求点D到平面ACE的距离。
平面BCE(2)求二面角B-AC-E的大小(3)求点D到平面ACE的距离。
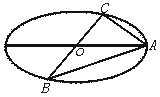
22.(本小题满分14分)已知A、B、C是长轴长为4的椭圆上的三点,点A是长轴的一个顶点,BC过椭圆中心O,如图,且![]() ·
·![]() =0,BC=2AC,
=0,BC=2AC,
(1)求椭圆的方程;
 (2)椭圆上是否存在两点P、Q使∠PCQ的平分线垂直AO,且PQ平行于AB,并说明理由.
(2)椭圆上是否存在两点P、Q使∠PCQ的平分线垂直AO,且PQ平行于AB,并说明理由.
参考答案
DCDAB BACCC DC
x=-6 ![]() 120º y2=4ax(a>0)
120º y2=4ax(a>0)
17.解:f(![]() )=1+z-
)=1+z-![]() f(-z)=1-z+
f(-z)=1-z+![]() …………2分
…………2分
设z=a+bi (a、b∈R) 由f(-z)=10+3i得
1-(a+bi)+a-bi=10+3i
即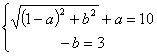 ………………6分
………………6分
解方程组得![]() …………………………10分
…………………………10分
所以复数z=5-3i……………12分
18.证明:如图,以D点为原点,建立空间直角坐标系,
(1)则![]()
![]() …………………………………………2分
…………………………………………2分
![]()
![]() ∴
∴![]()
![]()
![]()
![]()
∴![]() ………………………………6分
………………………………6分
(2)![]()
![]()
![]()
![]() …………………………………………………………8分
…………………………………………………………8分
![]()
![]()
![]()
![]()
![]()
![]()
![]()
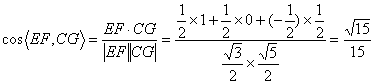
故EF与CG所成角的余弦值为![]() …………………………………………12分
…………………………………………12分
19. 解:由题意知直线OD的斜率为![]()
![]() ,所以直线AB的斜率为-2,且过D点,
,所以直线AB的斜率为-2,且过D点,
∴直线AB的方程为2x+y-5=0,………………………………2分
与y2=2px联立消去x得
y2+py-5p=0…………………………………4分
设A(x1,y1), B(x2,y2)则因![]() ⊥
⊥![]() ,所以x1x2+y1y2=0……………………6分
,所以x1x2+y1y2=0……………………6分
∵y1+y2=-p,y1y2=-5p,
x1x2=![]() …………………………8分
…………………………8分
![]() -5p=0得p=
-5p=0得p=![]() ………………………10分
………………………10分
所以所求抛物线的方程为y2=![]() ………………………………12分
………………………………12分
20. 解:存在,
当n=1时22=1×2×(a+b) 得a+b=2
当n=2时 22+42=2×3(2a+b) 得6a+3b=10
所以得a=![]() b=
b=![]() …………………………………4分
…………………………………4分
证明:⑴当n=1时,由以上知等式成立…………………6分
⑵ 假设当n=k时等式成立,即
22+42+62+…+(2k)2=k(k+1)( ![]() k+
k+![]() )
)
则22+42+62+…+(2k)2+[2(k+1)]2= k(k+1)( ![]() k+
k+![]() )+[2(k+1)]2…………8分
)+[2(k+1)]2…………8分
=(k+1)( ![]() k2+
k2+![]() k+4k+4)=(k+1)(
k+4k+4)=(k+1)( ![]() k2+
k2+![]() k+4)=(k+1)(k+2)(
k+4)=(k+1)(k+2)( ![]() k+2)
k+2)
=(k+1)[(k+1)+1] [![]() (k+1)+
(k+1)+ ![]() ]
]
所以当n=k+1时等式也成立.…………………………10分
由⑴⑵知对于任意正整数n等式22+42+62+…+(2n)2=n(n+1)( ![]() n+
n+![]() )都成立…12分
)都成立…12分
21.(1)证明:∵BF![]() 平面ACE ∴BF
平面ACE ∴BF![]() AE
AE
∵D-AB-E是直二面角 CB![]() AB
AB
∴CB![]() 平面ABE
平面ABE
∴CB![]() AE CB
AE CB![]() BF=B
BF=B
∴AE![]() 平面BCE……………………………………3分
平面BCE……………………………………3分
(2)以线段AB的中点O为原点,建立空间直角坐标系
![]()
![]()
![]()
则AE=(1,1,0) AC=(0,2,2)………………………………5分
![]() 设平面AEC的一个法向量n =(x,y,z)
设平面AEC的一个法向量n =(x,y,z)
![]()
![]()
![]()
![]()
![]()
![]() 则
则 ![]() 即
即 ![]()
![]()
![]() 令x=1 得n(1,-1,1)
令x=1 得n(1,-1,1)
又设平面BAC的一个法向量为m(1,0,0)……………………7分
![]()
![]()
![]()
![]() Cos<m,n>=
Cos<m,n>=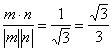
故二面角B-AC-E的大小为arccos![]() …………………………9分
…………………………9分
![]()
![]()
![]() (3)AD∥E轴,
(3)AD∥E轴,![]() AD=(0,0,2)
AD=(0,0,2)
![]()
![]()
![]()
![]()
![]()
![]()
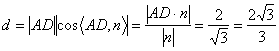
故点D到ACE之距为![]() ………………………………12分
………………………………12分
22.(1)由已知可得点A(-6,0),F(4,0)
设点P(x,y),则![]() =(x+6,y),
=(x+6,y),![]() =(x-4,y), ……………2分
=(x-4,y), ……………2分
由已知可得
![]()
![]()
(x+6)(x-4)+y2=0
则2x2+9x-18=0,x=![]() 或x=-6. ……………4分
或x=-6. ……………4分
由于y>0,只能x=![]() ,于是y=
,于是y=![]() .
.
∴点P的坐标是(![]() ,
,![]() )……………6分
)……………6分
(2) 直线AP的方程是x-![]() y+6=0. ……………8分
y+6=0. ……………8分
设点M(m,0),则M到直线AP的距离是![]() .
.
于是![]() =
=![]() ,又-6≤m≤6,解得m=2. ……………10分
,又-6≤m≤6,解得m=2. ……………10分
椭圆上的点(x,y)到点M的距离d有
d2=(x-2)2+y2=x2-4x+4+20-![]() x2=
x2=![]() (x-
(x-![]() )2+15,
)2+15,
由于-6≤x≤6, ∴当x=![]() 时,d取得最小值
时,d取得最小值![]() ……………14分
……………14分
解(1)以O为原点,OA所在的直线为x轴建立如图所
示的直角坐标系
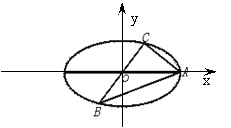 则A(2,0),设所求椭圆的方程为:
则A(2,0),设所求椭圆的方程为:![]() =1(0<b<2),
=1(0<b<2),
由椭圆的对称性知OC=OB,由![]() ·
·![]() =0得AC⊥BC,
=0得AC⊥BC,
∵BC=2AC,∴OC=AC,
∴△AOC是等腰直角三角形,∴C的坐标为(1,1),
∵C点在椭圆上
∴![]() =1,∴b2=
=1,∴b2=![]() ,所求的椭圆方程为
,所求的椭圆方程为![]() =1
……………6分
=1
……………6分
(2)由于∠PCQ的平分线垂直OA(即垂直于x轴),不妨设直线PC的斜率为k,则直线QC的斜率为-k,直线PC的方程为:y=k(x-1)+1,直线QC的方程为y=-k(x-1)+1, ……………8分
由![]() 得:(1+3k2)x2-6k(k-1)x+3k2-6k-1=0(*) ……………10分
得:(1+3k2)x2-6k(k-1)x+3k2-6k-1=0(*) ……………10分
∵点C(1,1)在椭圆上,∴x=1是方程(*)的一个根,则其另一根为![]() ,设P(xP,yP),Q(xQ,yQ),xP=
,设P(xP,yP),Q(xQ,yQ),xP=![]() , 同理xQ=
, 同理xQ=![]() ,
,
kPQ=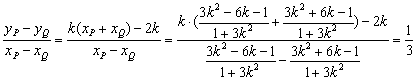 ………12分
………12分
而由对称性知B(-1,-1),又A(2,0) ∴kAB=![]()
∴存在两点P、Q使∠PCQ的平分线垂直AO,且PQ平行于AB。………14分