长泰二中2005/2006学年高二下学期第一次月考试卷

一、选择题：本大题共12小题；每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．两条异面直线指的是　　　　　　　　　　　　　　　　　　　　（　　）

　　A．没有公共点的两条直线

　　B．分别位于两个不同平面内的两条直线

　　C．某一平面内的一条直线和这个平面外的一条直线

　　D．不同在任何一个平面内两条直线

2．下列四个命题中，不正确的命题是　　　　　　　　 　　　　　　(　　)

A.如果一条直线与两条平行直线中的一条垂直，那么也和另一条垂直

B.已知直线ａ、ｂ、ｃ，ａ∥ｂ，ｃ与ａ、ｂ都不相交，若ｃ与ａ所成的角为θ，则ｃ与ｂ所成的角也等于θ

C.如果空间四个点不共面，则四个点中可能有三个点共线

D.若直线ａ∥平面α，点P∈α，则过P作ａ的平行线一定在α内

3．在空间四边形ABCD的边AB、BC、CD、DA上分别取点E、F、G、H，若EF与HG相交于一点M，则M 　　（　　）

A．一定在直线AC上

B．一定在直线BD上

C．可能在直线AC上，也可能在直线BD上

D．不在直线AC上，也不在直线BD上

4．已知下列四个命题：

（1）直线与平面没有公共点，则直线与平面平行

（2）直线上有两点到平面距离（不为零）相等，则直线与平面平行

（3）直线与平面内的任意一条直线不相交，则直线与平面平行

（4）直线与平面内的无数条直线不相交，则直线与平面平行，

其中正确命题为　　　　　　　　　　　　　　　　　　　　　　　 （　　）

A．（1）（2）　 B．（1）（3）  C．（1）（2）（3）   D．（1）（2）（3）（4）

5．正方体ABCD—A₁B₁C₁D₁中，与A₁B所成的角为45°的棱有　　　　　 （　　）

　　A．2条　　　　 B．4条　　　　 C．6条　　　　 D．8条

6．已知E、F、G、H是空间四点，设命题甲：点E、F、G、H不共面；命题乙：直线EF与GH不相交，那么甲是乙的　　　　　　　　　　　　 （　　）

A．充分不必要条件　　　　　　　 B．必要不充分条件

C．充要条件　　　　　　　　　　 D．不充分不必要条件

7．已知a、b是异面直线，，则直线C　　　　  （　　）

　　A．必与a、b都相交　　　　　　　B．至多与a、b中的一条平行

　　C．至多与a、b中的一条相交　　　D．至少与a、b中的一条平行

8．下列命题中，不正确的是　　　　　　　　　　　　　　　　　　　 （　　）

　　A．若一条直线垂直于一个平面，则这直线必垂直于这个平面内的任意直线

　　B．若一个平面过另一个平面的一条垂线，则这两个平面垂直

　　C．若一条直线和一个平面的一条斜线垂直，则这条直线必与斜线在这个平面内的射影垂直

　   D．若一条直线与两个平行平面中的一个垂直，则必与另一个也垂直

9．空间四边形ABCD的两对边AB=CD=3，E、F分别是AD、BC上的点，且AE∶ED=BF∶FC=1∶2，EF=，则AB与CD所成角的大小为　　　　　 （　　）

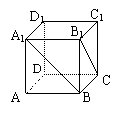A．30°　　　　 B．45°　　　　 C．60°　　　　 D．90°

10．如图正方体中，直线与所成的角的大小为　 （　　）

A．　　 　 B．　　　C．　　　　D．

11．若a, b是异面直线，那么经过b的所有平面中（　　）

　　A．只有一个平面与α平行　B．只有一个平面与α垂直

  　C．有无数个平面与α平行  D．有无数个平面与α垂直

12．如图，正方体ABCD－A₁B₁C₁D₁中，点P在侧面BB₁C₁C及其面界上运动，并且保持AP⊥BD₁，则动点P的轨迹是　　　　　　  （　　）

　　A．线段B₁C　　　　　　　　　　　B．线段BC₁　

C．BB₁中点与CC₁中点连成的线段　D．BC中点与B₁C₁中点连成的线段

二、填空题：本大题共4小题；每小题5分，共20分.把答案填在题中横线上.

13．没有公共点的两条直线的位置关系是　　　　　　　　  .

14．空间两个角∠ABC和∠，若AB//，BC//，∠ABC=40°，则∠的大小是　　　　　　　　 .

15．正方体ABCD—A₁B₁C₁D₁中，E为DD₁的中点，则BD₁与过点A、E、C的平面的位置关系是　　　　　  .

16．设E、F、G、H顺次为空间四边形ABCD各边的中点，且EG=3，HF=4，则AC²+BD²的值是　　　　　　　  .

三、解答题：本大题共6小题；共70分.解答应写出文字说明、证明过程或演算步骤.

17．（本小题满分9分）已知a、b是异面直线，直线c//a，且c不与b相交，求证：b、c是异面直线.

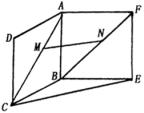
18．（本小题满分9分）如图，ABCD和ABEF都是正方形，，且．证明：平面BCE．

19．（本小题满分12分）空间四边形ABCD中，AB=CD且AB与CD所成的角为30°，E、F分别是BC、AD的中点，求EF与AB所成的角的大小.

20．（本小题满分12分）如图，已知：PA⊥PB，PA⊥PC，PB⊥PC，求证：△ABC是锐角三角形．

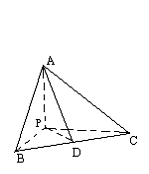
　 21．（本小题满分14分）如图，P是△ABC所在平面外一点，PA=PB，CB⊥平面PAB，M是PC的中点，N是AB上的点，AN=3NB，

　 （1）求证：MN⊥AB；

　 （2）当∠APB=90°，BC=2，AB=4时，

求MN的长。

22．（本小题满分14分）空间四边形ABCD中，点M、N、P、Q分别在AB、BC、CD、DA上满足.　 ①求证：M、N、P、Q四点共面；

②当对角线AC=6，BD=3，且MNPQ为正方形时，求AC与BD所成角的大小及k的值.

高二下学期第一次月考试卷

参考答案

一、1.D  2.C　3.A　4.B  5.D　6.A　7.B  8.C　9.C　10.C　11.A  12.A

二、13.平行或异面；14. 40°或140°；15. 平行；16. 50

三、17．假设b、c不是异面直线，则b、c共面………………………………2分

由于c与b不相交，则b//C　而c//a　∴a//b这与已知a、b是异面直线矛盾.故假设不成立，因此b、c

是异面直线……………………………………………………………………9分

18．作交BC于G，作交BE于H．

连结GH，则CM：CA=MG：AB，BN：BF=NH：EF，又，故，

于是，且．∴MNGH为平行四边形，故．

平面BCE，平面BCE，　 ∴平面BCE．………………9分

19．取BD的中点G，连结EG，FG，则EG//AB，FG//CD，∴∠FEG、∠EGF分别为EF与AB、AB与CD

所成的角，∵AB与CD所成的角为30°，∴∠EGF=30°或150°………5分　

在△EGF中，EG=FG=AB=CD，∴∠GEF=15°或75°即EF与AB所成的角为…15°或75°…………9分

20．由已知可得PA⊥平面PBC．在直角三角形PBC中，作PD⊥BC于D，因为∠PBC，∠PCB都是锐角，所以垂足D一定在斜边BC内部，连PD，则PD⊥BC（三垂线定理）．对于△ABC来说，因垂足D在BC边内部，所以∠ABC，∠ACB都是锐角，同理可证∠BAC也是锐角．………………………………………………12分

21．（1）取AB中点Q，连PQ,CQ,,

从而，

又

…………………………………7分

（2）

…………………………………14分

22．①∵∴MQ//BD且MQ=BD，同理NP//BD且NP=BD

　　于是MQ∥NP　 故M、N、P、Q四点共面……………………………7分

②由已知条件有　∴MN//AC　又NP//BD

∴MN与NP所成的角等于AC与BD所成的角，即∠MNP.

当MNPQ为正方形时，∠MNP=90°……………………………………10分

又当AC=6，BD=3，MNPQ为正方形时，MN=NP.　∴　

∴k=2………………14分