2005--2006年度株洲市第十七中学高二数学
期终检测题一
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案的代号填在题后的括号内。(每小题5分,共50分)
1.若![]() 的取值范围是( B )
的取值范围是( B )
A (-1,1) ; B (-1,0)∪(1,+∞) C (-1,0)∪(0,1) D (-∞,-1)∪((0,1).
2.![]() 是使
是使![]() 上恒成立的(B )
上恒成立的(B )
A.充分不必要条件 B.必要不充分条件 C. 充要条件 D.既不充分也不必要条件
3.直线![]() 与
与![]() 互相垂直,则实数
互相垂直,则实数![]() (A)
(A)
A.![]() B.1.5
C.-1.5
D.
B.1.5
C.-1.5
D.![]() 。
。
4.曲线![]() 与曲线
与曲线![]() 的( B )
的( B )
(A) 长、短轴相等 (B) 焦点相同 (C) 离心率相等 (D) 准线相同。
5.已知双曲线![]() 的一条准线为
的一条准线为![]() ,则该双曲线的离心率为(A )
,则该双曲线的离心率为(A )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
6.若双曲线的一条准线方程是13![]() =144,一条渐近线的方程是5
=144,一条渐近线的方程是5![]() ,则其标准方程是( A )
,则其标准方程是( A )
A ![]() B
B ![]() C
C ![]() D
D ![]()
7.已知圆心在抛物线![]()
![]() 上,且与抛物线
上,且与抛物线![]() 的准线及
的准线及![]() 轴都相切的圆方程是(B )
轴都相切的圆方程是(B )
A ![]() B
B ![]()
C ![]() D
D ![]()
8.已知两点A(-6,0)、B(0,8),点P在直线AB上,且![]() ,则点P到直线
,则点P到直线![]() 的距离为( A )。
的距离为( A )。
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 。
。
9、已知直线![]() 与曲线
与曲线![]() 有公共点,则截距
有公共点,则截距![]() 的取值范围是(B )
的取值范围是(B )
A ![]() B
B![]() ; C
; C ![]() D
D ![]()
10、已知F1、F2是双曲线![]() 的两焦点,以线段F1F2为边作正三角形MF1F2,若边MF1的中点在双曲线上,则双曲线的离心率是 ( D )
的两焦点,以线段F1F2为边作正三角形MF1F2,若边MF1的中点在双曲线上,则双曲线的离心率是 ( D )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 。
。
二、填空题:请把答案填在题中横线上(每小题6分,共计30分)。
11、不等式x-1+x-3![]() 在R上的解集是
在R上的解集是![]() ,则实数
,则实数![]() 的取值范围是_
的取值范围是_![]() ___.
___.
12、已知两直线y=x+2与y=2x+a+1的交点在圆![]() 的内部,则a 的取值范围是__(1,3)__
的内部,则a 的取值范围是__(1,3)__
13、圆(x-3)2+(y-4)2=25与圆(x-1)2+(y-2)2=r2(r>0)相切,则r的值是 ![]()
14.建造一个容积为18M3,深为2M的长方体无盖水池,如果池底和池壁每平方米的造价分别为200元和150元,那么这个水池的最低造价为 5400元 .
15、)以下四个关于圆锥曲线的命题中:
①设A、B为两个定点,k为非零常数,![]() ,则动点P的轨迹为双曲线;
,则动点P的轨迹为双曲线;
②过定圆C上一定点A作圆的动点弦AB,O为坐标原点,若![]() 则动点P的轨迹为椭圆;
则动点P的轨迹为椭圆;
③方程![]() 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;
④双曲线![]() 有相同的焦点.
有相同的焦点.
其中真命题的序号为 ③④ (写出所有真命题的序号)
三、解答题:解答应写出文字说明、证明过程或演算步骤.(共6小题,计70分)
16、(本题满分10分)
已知双曲线的离心率为2,求此双曲线的两渐近线的夹角。
答案:600。
17.(本题满分10分) 已知抛物线 ![]() +1,定点A(3,1),B为抛物线上任一点,点P在线段AB上,且满足
+1,定点A(3,1),B为抛物线上任一点,点P在线段AB上,且满足![]() ,当B点在抛物线上运动时,求P点的轨迹方程。
,当B点在抛物线上运动时,求P点的轨迹方程。
答案:![]() 。
。
18、(本题满分12分) 某工厂用同一种矿石生产甲、乙两种产品,已知生产甲种产品需矿石4T,煤3T;生产乙种产品需矿石5T,煤10T;已知每一吨甲种产品的利润是7万元,每一吨乙种产品的利润是12万元,工厂在生产这两种产品的计划中要求消耗这种矿石不超过200T,煤不超过300T,问甲、乙两种产品各生产多少时,才能使利润总额最大?
解:设生产甲种产品![]() T,乙种产品
T,乙种产品![]() T,利润总额为
T,利润总额为![]() 万元,则可得下列线性约束条件:
万元,则可得下列线性约束条件: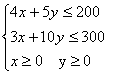 目标函数为
目标函数为![]() ,作出以上不等式组所表示的平面区域图(图略)
,作出以上不等式组所表示的平面区域图(图略)
作直线L:![]() ,把直线L向右上方平移到L1的位置时,直线通过可行域上的4x+5y=200与 3x+10y=300的交点P20,24)时,目标函数为
,把直线L向右上方平移到L1的位置时,直线通过可行域上的4x+5y=200与 3x+10y=300的交点P20,24)时,目标函数为![]() 取得最大值,所以应生产甲种产品20T,乙种产品20T,才能使利润总额最大。
取得最大值,所以应生产甲种产品20T,乙种产品20T,才能使利润总额最大。
19.(本题满分12分) 如果实数![]()
![]() 满足
满足![]() ,求:
,求:
(1)![]() 的最大值; (2)
的最大值; (2)![]() 的最小值。
的最小值。
答案:(1)![]() ;(2)
;(2)![]() 。
。
20.(本题满分12 分) 设G、M分别为不等边△ABC的重心与外心,A(-1,0)、B(1,0),且
![]() ,
,
求:(1)点C的轨迹E的方程;
(2)直线![]() 过(0,1)并与曲线E交于P、Q两点,且满足
过(0,1)并与曲线E交于P、Q两点,且满足![]() ,求直线
,求直线![]() 的方程。
的方程。
解:(1)设C(![]() ),则G(
),则G(![]() ),其中
),其中![]() ,设外心M(0,
,设外心M(0,![]() ),因
),因![]() ,
,![]() ,即
,即![]() 。
。
由![]() ,
,![]() 得
得![]() ,整理得:
,整理得:
![]() (
(![]() )即为所求的轨迹方程。
)即为所求的轨迹方程。
(2)由已知直线![]() 的斜率存在,设
的斜率存在,设![]() :
:![]() 代入
代入![]() 中,化简得
中,化简得![]() ,
,
![]() 。
。
设P![]() 、Q
、Q![]() ,
,![]() ,由
,由![]()
![]()
由此得到![]()
![]()
![]() ,所以
,所以
直线![]() 的方程:
的方程:![]()
21.(本题满分14分) 已知椭圆C:![]() +
+![]() =1(a>b>0)的左.右焦点为F1、F2,离心率为e. 直线l:y=ex+a与x轴.y轴分别交于点A、B,M是直线l与椭圆C的一个公共点,P是点F1关于直线l的对称点,设
=1(a>b>0)的左.右焦点为F1、F2,离心率为e. 直线l:y=ex+a与x轴.y轴分别交于点A、B,M是直线l与椭圆C的一个公共点,P是点F1关于直线l的对称点,设![]() =λ
=λ![]() .
.
(Ⅰ)证明:λ=1-e2;
(Ⅱ)若![]() ,△MF1F2的周长为6;写出椭圆C的方程;
,△MF1F2的周长为6;写出椭圆C的方程;
(Ⅲ)确定λ的值,使得△PF1F2是等腰三角形.
解:
(Ⅰ)因为A、B分别是直线l:![]() 与x轴、y轴的交点,所以A、B的坐标分别是
与x轴、y轴的交点,所以A、B的坐标分别是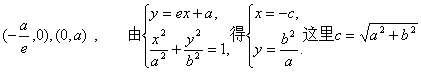 .
.
所以点M的坐标是(![]() ). 由
). 由![]()
即
(Ⅱ)当![]() 时,
时,![]() ,所以
,所以![]() 由△MF1F2的周长为6,得
由△MF1F2的周长为6,得![]()
所以![]() 椭圆方程为
椭圆方程为![]()
(Ⅲ)因为PF1⊥l,所以∠PF1F2=90°+∠BAF1为钝角,要使△PF1F2为等腰三角形,必有PF1=F1F2,即![]()
设点F1到l的距离为d,由![]()
得![]() 所以
所以![]()
即当![]() △PF1F2为等腰三角形.
△PF1F2为等腰三角形.
