2005——2006学年高二第一学期期末考试数学试题
（时间90分钟，满分100分）
| 题号 | 一 | 二 | 三 | 总分 | ||||
| 1—10 | 11—14 | 15 | 16 | 17 | 18 | 19 | ||
| 得分 | ||||||||
一、填空题（本题共10小题，每小题3分，满分30分）
1.若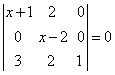
，则
.
2.若
是某三角形的两个内角，且行列式
，则
的值为 .
3.已知
，若
，则实数
的值为 .
4.若
，且
，则向量
与
的夹角为 .
5.一架飞机向东飞行100千米，然后改变方向向南飞行100千米，则这架飞机两次位移的和为 .(精确到千米)
6.已知点
与
，且
.则
所在直线
的点方向式方程为
.
7.经过点
，且与向量
垂直的直线的点法向量式方程为
.
8.与双曲线
有共同的焦点，且经过点
的椭圆的标准方程为 .
9.椭圆
的一个焦点是
，那么
.
10.对于顶点在原点的抛物线，给出下列条件：
（1）焦点在
轴上；
（2）焦点在
轴上；
（3）抛物线上横坐标为1的点到焦点的距离为3；（4）焦点到准线的距离为4；
（5）由原点向过焦点的某直线作垂线，垂足坐标为
.
能使抛物线方程一定为
的条件是
（要求填写合适条件的序号）
二、选择题（本题共4小题，每小题4分，满分16分）
11.下列命题正确的是 ( )
A.如果
，那么
或
； B.如果
都是非零向量，那么
；C.如果
，那么
或
； D.如果
，那么或
.
12.已知两点
，则过点
的直线的倾斜角为 ( )
A.
B.
C.
D.
13.已知两个观察站
相距1千米.一炮弹在某处
爆炸，在
处听到爆炸声的时间比
处快2秒钟，则点一定在
( )
A.以为焦点的双曲线的左半支上 B.以为焦点的右半支上
C.以为焦点的椭圆上
D.在向量
的延长线上
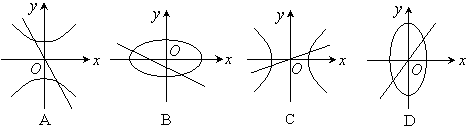
14.设
是非零实数，则方程
及
所表示的图形可能是( )
三、解答题（本题共5题，满分54分）
15.（本题满分10分）
已知两条直线
，试讨论直线
与
之间的位置关系.
16.(本题满分10分)
已知定圆
，动圆
和已知圆内切，且过点
，求圆心的轨迹及其方程.
17.(本题满分10分)
已知双曲线的一条渐近线方程是
，若双曲线经过点
，求双曲线的标准方程.
18. (本题满分12分)
设坐标原点为
，抛物线
与过焦点的直线交于.试求向量
与
的数量积.
19. (本题满分12分)
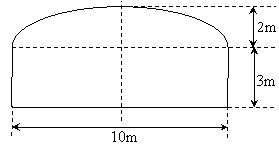
一段双行道隧道的横截面边界由椭圆的上半部分和矩形的三边组成，如图所示.一辆卡车运载一个长方形的集装箱，此箱平放在车上与车同宽，车与箱的高度共计4.2米，箱宽3米，若要求通过隧道时，车体不得超过中线.试问这辆卡车是否能通过此隧道，请说明理由.
参考答案
选择题：1.
或
2.
3. 4.
5.东偏南
方向141千米
6.
7.
8.
9.
10.(1)(3)或(1)(5)或(1)(3)(4)或(1)(4)(5)
11.C 12.D 13.A 14.C
15.当
且
时，直线与相交；
当
时，直线与平行；当
时，直线与重合.
16.圆心的轨迹是以
为焦点的椭圆，且其方程为
.
17.双曲线的标准方程是
.
18.
.
19.建立如图所示的坐标系，则此隧道横截面的椭圆上半部分方程为：
.
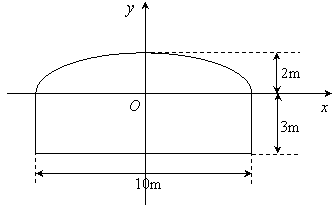令
，则代入椭圆方程，解得
，
因为
，
所以，卡车可能通过此隧道.