襄樊市高中调研测试题(2005.6)
高 二 数 学(理科)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．第Ⅰ卷1至2页，第Ⅱ卷3至8页，共150分，考试时间120分钟．
第 Ⅰ 卷(选择题，共60分)
注意事项：
1．请考生将自己的学校、班级、姓名、学号填写在第Ⅱ卷密封线内．
2．每小题选出答案后在第Ⅱ卷前的答题栏内用2B铅笔把对应题目的答案代号涂黑，如需改动，必须用橡皮擦干净后，再选涂其它答案，不能答在试题卷上．
参考公式：
|
、c分别表示上、下底面周长，l表示斜高或母线长
|
一．选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．
1. 如果事件A、B互斥，那么
A．
是必然事件 B．
是必然事件
C．A与
是互斥事件 D．
与是互斥事件
2.
条件甲：直线a、b是异面直线；条件乙：两条直线a 、b 无公共点，则甲是乙的
A．充分非必要条件 B．必要非充分条件
C．充要条件 D．既非充分又非必要条件
3.
展开式中，二项式系数最大的项是
A．第n－1项 B．第n项
C．第n－1项与第n＋1项 D．第n项与第n＋1项
4.
从4名男生和3名女生中选出4人参加某个座谈会，若这4人中必须既有男生又有女生，则不同的选法共有
A．140种 B．120种 C．35种 D．34种
5.
在今年公务员录用中，某市农业局准备录用文秘人员二名，农业企业管理人员和农业法宣传人员各一名，报考农业公务员的考生有10人，则可能出现的录用情况种数是
A．5040 B．2520 C．1260 D．210
6.
在下列条件中，使M与A、B、C一定共面的是
A．
B．
C．
D．
7.
在正方体ABCD－A
BCD中，与对角线AC1异面的棱有
A．12条 B．6条 C．4条 D．2条
8.
排一张有5个独唱和3个合唱的节目表，如果合唱不排两头，且任何两个合唱不相邻，则这种事件发生的概率为
A．1 B．
C．
D.
9.
一个棱长为1的正方体，截去一个正棱锥形状的角，剩余几何体的体积最小可能是
A．
B．
C．
D．不能确定
|
|
10.
过球面上三点A、B、C的截面和球心的距离等于球半径的一半，且AB＝BC＝CA＝a，则球的表面积是
A．
B．
C．
D．
11.
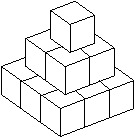
把14个棱长为1的正方体，在地面上堆叠成如图所示的几何体，然后将露出的表面部分染成红色，那么红色部分的面积为
A．37 B．33
C．24 D．21
12.
计算1！+ 2！+ 3！+ …… + 100！得到的数，其个位数字是
A．2 B．3 C．4 D．5
第Ⅰ卷答题栏
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | ||||
[ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | ||||
[ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | ||||
[ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | ||||
| [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] |
襄樊市高中调研测试题(2005.6)
高 二 数 学(理科)
第 Ⅱ 卷(非选择题，共90分)
注意事项：
第Ⅱ卷共6页，用黑色签字笔直接答在试题卷中，答卷前将密封线内的项目填写清楚．
| 题 号 | 一 | 二 | 三 | 总 分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | ||||
| 得 分 | |||||||||
| 得分 | 评卷人 |
二．填空题：本大题共4小题，每小题4分，共16分．将正确答案填在题中横线上．
13.
已知
……
，那么x被7除的余数为 ．
14. 将标号为1，2，……，10的10个球放入标号为1，2，……，10的10个盒子内，每个盒子内放一个球，则恰好有3个球的标号与其所在盒子的标号不一致的放入方法共有_______________种(以数字作答)．
15. 口袋中有红球2个，黑球3个，白球5个，它们只有颜色不同．从中摸出四个，摸出的球中同色的两个为一组，若红色一组得5分，黑色一组得3分，白色一组得1分，则得分总数取得最大值的概率为________________．
16. 设l、m、n是三条不同的直线，
是三个不同的平面，下面有四个命题：
①若l∥
，
∥，则l∥ ②l∥n，m∥n，则l∥m
③若
，l∥，则
④若
，
，，则l⊥m
其中正确命题的序号有 ．
三．解答题：本大题共6小题，满分74分．
| 得分 | 评卷人 |
17.
(本大题满分12分)已知
的展开式中，前三项系数的绝对值依次成等差数列．
(1)证明：展开式中没有常数项；
(2)求展开式中所有有理项．
| 得分 | 评卷人 |
18.
(本大题满分12分)已知平面∥平面，直线a与平面相交，求证：直线a与平面相交．
19.
(本大题满分12分)某网络安全中心同时对甲、乙、丙三个网络系统的安全进行监控，以便在发现黑客入侵时及时跟踪锁定．今测得在一段时间内，甲、乙、丙三个网络系统各自遭受到黑客入侵的概率分别为0.1、0.2、0.15．
(1)求三个网络系统都受到黑客入侵的概率；
(2)求只有一个网络系统受到黑客入侵的概率．
| 得分 | 评卷人 |
20.
(本大题满分12分)如图，ABCD为矩形，PA⊥平面ABCD，M、N分别是AB、PC中点．
(1)求证：MN⊥AB；
(2)若平面PDC与底面ABC所成角为
，能否确定，使MN是异面直线AB与PC的公
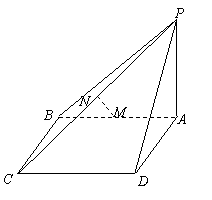垂线，若能求出；若不能说明理由．
| 得分 | 评卷人 |
21.
(本大题满分12分)如图，设ABCDEF为正六边形，一只青蛙从顶点A开始随机跳动，每次随机地跳到与它所在顶点相邻的两顶点之一，每次按顺时针方向跳动的概率为．
(1)求青蛙从A点开始经过3次跳动所处的位置为D点概率；
(2)求青蛙从A点开始经过4次跳动所处的位置为E点概率．
| 得分 | 评卷人 |
|
|
22. (本大题满分14分)如图，已知正方形ABCD和矩形ACEF所在的平面互相垂直，
AB＝
，AF＝1，M是线段EF的中点．
(1)求证AM∥平面BDE；
(2)求二面角A—DF—B的大小；
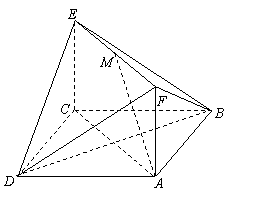(3)试在线段AC上确定一点P，使得PF与CD所成的角是60°．
| 得分 | 评卷人 |