襄樊市高中调研测试题(2005.6)
高二数学(理科)参考答案及评分标准
命题人:襄樊市教学研究室 郭仁俊
说明:
1.本解答指出了每道题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.
2.对计算题当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定给分,但不得超过该部分正确解答应得分数的一半;如果后续部分的解答有较严重的错误,就不再给分.
3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.
4.只给整数分数,选择题和填空题不给中间分数.
一.选择题:BADD BCBC CDBB
二.填空题:13.5 14.240 15.![]() 16.②④
16.②④
三.解答题:
17.(1)证:前三项系数的绝对值是1,![]()
依题意有![]() 2分
2分
即n2-9n+8=0,解得n=8,n=1(舍去) 4分
![]() 6分
6分
当且仅当![]() 时,
时,![]() 是常数,这时3r=16,
是常数,这时3r=16,
∵r∈Z,∴3r=16不可能,∴展开式中没有常数项. 8分
(2)若![]() 为有理项,则
为有理项,则![]() 为整数
为整数
∵0≤r≤8,r∈Z,∴r=0,4,8 10分
即展开式中的有理项共有三项,它们是:![]() . 12分
. 12分
18.证法一:设直线a与平面![]() 相交于点A,在平面
相交于点A,在平面![]() 取一点B
取一点B
若点B在直线a上,则直线a与平面![]() 相交于点B 4分
相交于点B 4分
若点B不在直线a上,则直线a和点B确定一个平面![]()
且平面![]() 与平面
与平面![]() 相交于过A点的直线b,平面
相交于过A点的直线b,平面![]() 与平面
与平面![]() 相交于过B点的直线c
相交于过B点的直线c
∵![]() ,∴b∥c 8分
,∴b∥c 8分
又在平面![]() 内,直线a与直线b相交,∴直线a与直线c相交于一点C
内,直线a与直线b相交,∴直线a与直线c相交于一点C
∵![]() ,∴
,∴![]() ,故直线a与平面
,故直线a与平面![]() 相交于C点. 12分
相交于C点. 12分
证法二:设a与![]() 不相交,则
不相交,则![]() 或
或![]() 2分
2分
(1)若![]() ,∵
,∵![]() ,∴
,∴![]() ,与“a与
,与“a与![]() 相交矛盾” 4分
相交矛盾” 4分
(2)若![]() ,过
,过![]() 作平面
作平面![]() ,使
,使![]() ∩
∩![]() =b,
=b,![]() ∩
∩![]() =c 6分
=c 6分
∵![]() ,∴
,∴![]() ,因此,
,因此,![]() 8分
8分
又∵![]() ,∴
,∴![]() ,与“a与
,与“a与![]() 相交矛盾” 11分
相交矛盾” 11分
由(1)(2)可得:a与![]() 相交 12分
相交 12分
19.(1)解:分别记甲、乙、丙三个网络系统在这段时间内受黑客入侵的事件为A、B、C
依题意:A、B、C三个事件相互独立 2分
∴在这段时间内三个网络系统都受到黑客入侵的概率为
P1=P(A ·B ·C)= P(A)
·P(B)·P(C)=0.1×0.2×0.15=0.003 5分
(2)解:在这段时间内只有一个网络系统受到黑客入侵为三个事件![]() 、
、![]() 、
、![]() 之一,且这三个事件彼此互斥 7分
之一,且这三个事件彼此互斥 7分
∴只有一个网络系统受到黑客入侵的概率为
P2=P(![]() +
+![]() +
+![]() )
)
=P(![]() )+P(
)+P(![]() )+P(
)+P(![]() ) 9分
) 9分
=0.1×(1-0.2)×(1-0.15)+(1-0.1)×0.2×(1-0.15)+(1-0.1)×(1-0.2)×0.15
=0.329 11分
答:在这段时间内三个网络系统都受到黑客入侵的概率为0.003,只有一个网络系统受到黑客入侵的概率为0.329 12分
20.方法一:(1)取CD边中点R,连结MR、NR,则NR∥PD,MR∥AD 2分
∵AB⊥AD Þ AB⊥MR
又PA⊥平面ABCD ,由三垂线定理知AB⊥PD Þ AB⊥NR
∴AB⊥面MNR
Þ AB⊥MN. 4分
(2)PA⊥平面ABCD,由三垂线定理知PD⊥CD,∴∠PDA=![]() 6分
6分
要使MN是AB与PC的公垂线,由(1)知MN⊥AB
∴只需MN⊥PC即可,又N是PC的中点,故只需CM=PM即可 8分
这时由于BM=AM,∠ABC=∠PAD=90°
∴△CBM≌△PAM,故PA=BC=AD
∴△PAD为等腰直角三角形,∴∠PAD=45° 10分
即当![]() =45°时可满足题意. 12分
=45°时可满足题意. 12分
方法二:以![]() 为x轴、y轴、z轴建立空间直角坐标系,设AB=a,AD=b,AP=c
为x轴、y轴、z轴建立空间直角坐标系,设AB=a,AD=b,AP=c
则B(a,0,0),C(a,b,0),D(0,b,0),P(0,0,c)
∴M(![]() ,0,0),N(
,0,0),N(![]() ),R(
),R(![]() )
)
故![]() ,
,![]() =(a,0,0),
=(a,0,0),![]() =(a,b,-c)
=(a,b,-c)
(1) ∵![]() ,∴AB⊥MN. 4分
,∴AB⊥MN. 4分
(2)由(1)知MN⊥AB,要使MN是AB与PC的公垂线,只需MN⊥PC即可.
若MN⊥PC,则![]() ,∴b=c 6分
,∴b=c 6分
即AD=AP,因此∠PDA=45° 8分
PA⊥平面ABCD,由三垂线定理知PD⊥CD
∴∠PDA=![]() ,即当
,即当![]() =45°时可满足题意. 12分
=45°时可满足题意. 12分
21.(1)解:设青蛙顺时针跳动1次为事件A,逆时针跳动1次为事件B,则
P(A)=![]() ,P(B)=1-P(A)=
,P(B)=1-P(A)=![]() 2分
2分
青蛙从A点开始经过3次跳动到达D点有两种方式:顺时针跳动3次或逆时针跳动3次
4分
故所求概率为P(A·A·A)+P(B·B·B)=![]() 6分
6分
(2)青蛙从A点开始经过4次跳动到达E点有两种方式:逆时针跳动4次,或顺时针跳动3次而逆时针跳动1次 8分
逆时针跳动4次的概率为![]()
顺时针跳动3次而逆时针跳动1次的概率为![]() 10分
10分
故所求概率为![]() . 12分
. 12分
|
|
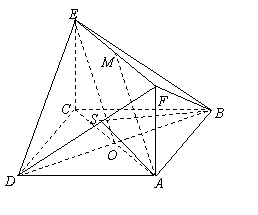
22.方法一:(1)记AC与BD的交点为O,连接OE,
∵O、M分别是AC、EF的中点,ACEF是矩形,
∴四边形AOEM是平行四边形,
∴AM∥OE. 2分
∵![]() 平面BDE,
平面BDE, ![]() 平面BDE,
平面BDE,
∴AM∥平面BDE. 4分
(2)在平面AFD中过A作AS⊥DF于S,连结BS,
∵AB⊥AF, AB⊥AD,
∴AB⊥平面ADF,
∴AS是BS在平面ADF上的射影,
由三垂线定理得BS⊥DF.
∴∠BSA是二面角A—DF—B的平面角. 6分
在RtΔASB中,![]() ,∴
,∴![]()
∴二面角A—DF—B的大小为60º. 8分
(3)设CP=t (0≤t≤2),作PQ⊥AB于Q,则PQ∥BC,
∴∠FPQ是PF与BC所成的角 10分
∵PQ⊥AB,PQ⊥AF,∴PQ⊥平面ABF,∴PQ⊥QF.
在RtΔPQF中,∠FPQ=60º,∴PF=2PQ. 12分
∵ΔPAQ为等腰直角三角形,∴![]()
又∵ΔPAF为直角三角形,∴![]() ,
,
∴![]() ,所以t=1或t=3(舍去)
,所以t=1或t=3(舍去)
即点P是AC的中点. 14分
|
|
方法二:(1)同方法一.
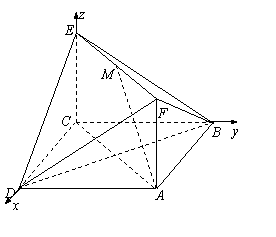
(2)以![]() 为x轴、y轴、z轴建立空间直角坐标系.则
为x轴、y轴、z轴建立空间直角坐标系.则
A(![]() ,
,![]() ,0),B(0,
,0),B(0,![]() ,0),D(
,0),D(![]() ,0,0),E(0,0,1),F(
,0,0),E(0,0,1),F(![]() ,
,![]() ,1),M
,1),M![]()
∵AF⊥AB,AB⊥AD,AF∩AD=A,
∴AB⊥平面ADF.
∴![]() 为平面DAF的法向量.
6分
为平面DAF的法向量.
6分
设平面BDF的法向量为n=(x,y,1),则
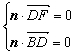 ,即
,即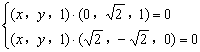 ,解得x=y=
,解得x=y=![]()
∴n=(![]() ,
,![]() ,1)
,1)
∴cos<![]() ,n>=
,n>=![]() ,∴
,∴![]() 与n的夹角是60º.
与n的夹角是60º.
即所求二面角A—DF—B的大小是60º. 8分
(3)设P(t,t,0) (0≤t≤![]() ),则
),则![]() ,
,![]() ,0,0)
,0,0)
∵PF和CD所成的角是60º.
∴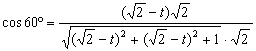 12分
12分
解得![]() 或
或![]() (舍去),即点P是AC的中点. 14分
(舍去),即点P是AC的中点. 14分