高二数学练习（十三）

一、选择题

1．经过（1，2）点的抛物线的标准方程是　　　　　　　　　　　　　　　　　  （　　）

  （A）y²＝4x　 （B）x²＝y　　(C) y²＝4x 或x²＝y　 (D) y²＝4x 或x²＝4y

2．动点P到直线x＋4=0的距离比到定点M(2, 0)的距离大2，则点P的轨迹是　　　　 （ 　 ）

　（A）直线　（B）圆　（C）抛物线　（D）双曲线

3．过抛物线y²=4x的顶点O作互相垂直的两弦OM、ON，则M、N的横坐标x₁与x₂之积为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

（A）4　　　（B）16　　　　（C）32　　　　 （D）64　　

4．过抛物线y²=8x上一点P(2, －4)与抛物线仅有一个公共点的直线有　　　　　  （ 　 ）

　（A）1条　　 （B）2条　　　（C）3条　　　 （D）1条或3条

5．直线与抛物线交于A、B两点，且AB中点的横坐标为2，则k的值为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

（A）或2　　　　　 （B）　　　　　　　（C）2　　　　　 （D）

6．在抛物线y²＝4x上有点Ｍ，它到直线y＝x的距离为４，如果点Ｍ的坐标为（a，b），

　 a、b∈R^＋，则的值为　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　（A）　　　　（B）　　　　　 　　　　　　　　　　 （C）１　　　　　  　 （D）２

7．平移抛物线y²=x，并使顶点在以(－1,0)，(0,2)为端点的线段上运动，则抛物线截直线y=x所得的线段长的最大值是　　　　　　　　　　　　　　　　　　　　　　　　　 （ 　 ）

  （A）　　 （B）　　　 （C）　　 　（D）3

8．抛物线与直线y＝k(x－1)的一个交点A的坐标是（4，4），点A到焦点的距离是 （A）4　　　　 （B）　　　　  （C）5　　　　  （D）6　　　　　　　 （　　） 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

9．若抛物线y＝2x²上两点A（x₁,y₁）、B（x₂,y₂）关于直线y＝x＋m对称，且x₁x₂＝－，则实数m的值为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

（A）　　　 （B）　　　　  （C）　　　　 （D）2

10．对于抛物线C：，若点M（x₀,y₀）在抛物线的内部（即），则直线l：y₀y＝2（x＋x₀）与抛物线C　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

  （A）恰有一个公共点　　　　　　　 （B）恰有两个公共点

（C）可能一个也可能两个公共点　　 （D）没有公共点

二、填空题

11．抛物线上的两点A,B的横坐标是关于x的方程x²+px+q=0(常数p,q∈R)的两个实根，则直线AB的方程是____________．

12．抛物线y=4x² 上的点到直线y=4x－5的最近距离是　　　　　　　 ．

13．直线x－2y－2=0与抛物线x=2y²交于A、B两点，F是抛物线的焦点，则△ABF的面积为　　　　　　　 ．

14．已知A、B是抛物线（p>0）上两点，O为坐标原点．若OA＝OB，且△AOB的垂心恰是此抛物线的焦点，则直线AB的方程是　　　　　　　　　  ．

15．设Ｏ为坐标原点，直线x＋2y－6＝0与抛物线y²＝2x相交于Ｐ、Ｑ两点，则

∠ＰＯＱ等于　　　　　　．

三、解答题

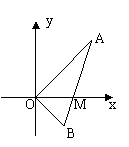
16．如图所示，线段AB过x轴正半轴上一点M（m，0），端点A、B到x轴的距离之积为2m，以x轴为对称轴，过A、O、B三点作抛物线，求该抛物线的方程．

17．过点P（0，4）作圆x²＋y²＝4的切线l，若l与抛物线（p>0）交于两点A、B，且OA⊥OB，求抛物线的方程．

18．在抛物线x²＝y＋1上三点A、B、C中，若A（－1，0），AB⊥BC，当点B在抛物线上移动时，求C的横坐标的取值范围．

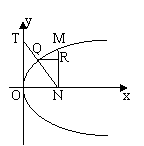19．若M是抛物线y²＝2px（p>0）上一点，MN⊥x轴于N，MN的垂直平分线交抛物线于点Q，直线NQ交y轴于点T．求证：OT＝MN．

20．已知抛物线y²＝4x的准线与x轴交于M点，过M作直线与抛物线交于A、B两点，若AB的垂直平分线与x轴交于E(x₀，0)．（1）求x₀的取值范围；（2）ΔABE能否是等边三角形？若能，求x₀的值；若不能，请说明理由．