高二数学练习（十四）

一、选择题

1．设圆C过双曲线的一个顶点和一个焦点，且圆心在该双曲线上，则圆心到该双曲线的中心的距离是　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

（A） 　　　　 （B）　　　　 （C）　　　　　 （D）5

2．已知M是抛物线y＝x²上的一个动点，以OM为边作一正方形MNPO，则动点P的轨迹方程为 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

 （A）y²＝x　　　 （B）y²＝－x　　　　（C）y²＝±x　　　 （D）x²＝±y

3．一动圆的圆心在抛物线上，且动圆恒与直线相切，则动圆必过定点

（A）（4，0）　　 （B）（0，–4）　 （C）（2，0）　（D）（0，–2）　　　　  （　　）

4．设动点P在直线上，O为坐标原点．以OP为直角边、点O为直角顶点作等腰，则动点Q的轨迹是　　　　　　　　　　　　　　　　　　　  　　　　　　　　　　　　　　　　　　　 （　　）

（A）圆　　　　 （B）两条平行直线　　　　　　（C）抛物线　　　　　　（D）双曲线

5．已知P是椭圆第三象限内一点，且它与两焦点连线互相垂直，若点P到直的距离不大于3，则实数m的取值范围是　　　　　　　　　　 　　　　　  　　　　　 （　　）

　　（A）[－7，8]　 （B）　 （C）[－2，2]　　（D） 　　　　　　　　　　　

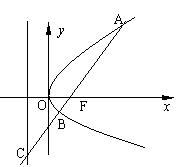
6．如图，过抛物线的焦点F的直线交抛

物线于点A、B，交其准线于点C，若，且，

则此抛物线的方程为　　　　　　　　　　　　  （　　）

　　（A） 　　　　　　　　　　　　　 （B） 　　

　　（C） 　　　　　　　　　　　　　 （D）　

7．已知c是椭圆(a＞b＞0)的半焦距，则的取值范围是　　 　　　 （　　）

　（A）(1，＋∞)　　　（B）（，＋∞)　 （C）(1，)　　 （D）(1,]

8．设椭圆和双曲线的公共焦点为F₁、F₂，P 是两曲线是一个公共点，则的值等于　　　　　　　　　　　　　　　　　　　　　　　 （　　）

（A）　 （B）　　（C）　　（D）

二、填空题

9．E、F是的左、右焦点，l是椭圆的一条准线，点P在l上，则∠EPF的最大值是　　　　　　　　　 ．

10．直线l：x－y＝2，点P（1，0）关于l的对称点P1在双曲线2ax²－ay²＝1上，则双曲线的焦点坐标是　　　　　　  　　．

11．抛物线y＝－与过点M（0，－1）的直线l相交于A、B两点，O为坐标原点，若直线OA与OB的斜率之和为1，则直线l的方程为　　　　　　　　　　  ．

12．以定直线l：x＝－2为准线，原点为相应的焦点的动椭圆的短轴MN的端点的轨迹方程为　　　　　　　　　　　　　  ．

三、解答题

13．设准线l：y＝x＋b与C：椭圆（a>1）相交于A、B两点，且l过椭圆C的右焦点，若以AB为直径的圆过椭圆的左焦点，试求该椭圆C的方程．

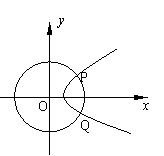14．设以原点为圆心，r为半径的圆与相交于P、Q两点，θ＝∠POQ（0<θ<π），问：当r为何值时，θ取得最大值？

15．QR是抛物线y²＝4x上垂直于对称轴的一条弦，P是抛物线上一点，直线PR与x轴交于点M，过PQ的直线交x轴于N，求证：抛物线的顶点O平分线段MN．

16．已知抛物线y²＝4x，椭圆，它们有共同的焦点F₂，若P是两曲线的一个公共点，且F₁是椭圆的另一个焦点，求△PF₁F₂的面积．

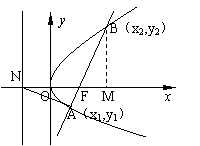17．已知抛物线，准线l与x轴交于N点，过焦点F作直线与此抛物线交于A（x₁,y₁）、B（x₂,y₂），使AB⊥AN，M是点B在x轴上的射影．（1）证明：4x₁x₂＝p²；（2） x₁－x₂的值（用p表示）；（3）求证：∠MAB＝∠MBA．