高二数学练习（十二）期末测试卷（2003-12-17）

学号　　　　姓名　　　 成绩　　　　  　　

一．选择题

1．圆x²＋y²＋2x＋6y＋9＝0与圆x²＋y²－6x＋2y＋1＝0的位置关系是　　　　　 （ 　　）

（A）相离　（B）相外切　（C）相交　（D）相内切

2．椭圆(1－m)x²－my²=1的长轴长是　　　　　　　　　　　　　　　 　　　　 （　　 ）

（A）　　（B）　　（C）　　（D）

3．椭圆的两个焦点和中心把两准线间的距离四等分，则一焦点与短轴两端点连线的夹角是　　　　　　　　　　　　　　　　　　　　　　　　  　 

　（A）　　  （B）　　  （C）　　　 （D）　　　　　　　　　　  （ 　　）

4．“ab<0”是“方程ax²+by²=c表示双曲线”的　　　　　　　　　　 　　　　 （ 　　）

　（A）必要不充分条件　　　　　　　　 （B）充分不必要条件

　（C）充要条件　　　　　　　　　　　 （D）非充分非必要条件

5．设F₁, F₂是椭圆的两个焦点，P在椭圆上，已知P, F₁, F₂是一个Rt△的三个顶点，且P F₁>P F₂，则P F₁ : P F₂的值是　　　　　　　　　　　　　　　　 （　　 ）

　（A）或2　　（B）或　　（C）或 　 （D）或2

6．已知点F(, 0)，直线l: x=－，点B是l上的动点，若过B垂直于y轴的直线与线段BF的垂直平分线相交于点M，则点M的轨迹是　　　　　　　　　　　　　　 （　　 ）

　（A）双曲线　　 （B）椭圆 　　（C）圆　　　（D）抛物线

7．直线x－2y－3=0与圆x²+y²－4x+6y+4=0交于A, B两点，C为圆心，则△ABC的面积是　　　　　　　　　　　　　  　　　　　　　　　　　　　　

　（A）2　（B）4　（C）　（D）2　　　　　　　　　　　 （ 　　）

8．以双曲线的右焦点为圆心，且与两条渐近线相切的圆的方程是　　（　 　）

　（A）(x+5)²+y²=9　　　　　　　（B）(x+5)²+y²=16

　（C）(x－5)²+y²=9 　　　　　　（D）(x－5)²+y²=16

9．若椭圆(m>n>0)与双曲线(s>0, t>0)有相同的焦点F₁和F₂(m≠s)，P是两曲线的一个公共点，则PF₁·PF₂的值是　　　　　　　 　　　　　　　　 （ 　　）

　（A）　　 （B）m－s　　　 （C） 　　 （D）

10．过P(1, 0)的直线l与抛物线y²=2x交于两点M, N，O为原点，若k_OM+k_ON=1，则直线l的方程是　　　　　　　　　　　　　　　　　　　　　　　  　　　　　　　　（ 　　）

　（A）2x－y－1=0  （B）2x+y+1=0　（C）2x－y－2=0  （D）2x+y－2=0

二．填空题：

11．若实数x, y满足(x－2)²+y²=1，则的取值范围是　　　　　　　　  ．

12．圆心在x轴上，经过原点，并且与直线y＝4相切的圆的一般方程是

　 　　　　　　　　　　　　　　　　　　　　　　　　　 ．

13．椭圆x²＋4y²=16被直线y=x＋1截得的弦长为　　　　　　　　　　　 ．

14．以抛物线y²=4x的焦点为圆心，且被抛物线的准线截得的弦长为2的圆的方程是　　　　　　　　　　　　　 ．

三．解答题：

15．已知圆的方程x²＋y²＝25，点A为该圆上的动点，AB与x轴垂直，B为垂足，点P分有向线段BA的比λ=．

（1） 求点P的轨迹方程并化为标准方程形式；

（2） 写出轨迹的焦点坐标和准线方程．

16．已知椭圆的中心在原点，焦点在x轴上，连接它的四个顶点得到的四边形的面积是4，分别连接椭圆上一点(顶点除外)和椭圆的四个顶点，连得线段所在四条直线的斜率的乘积为，求这个椭圆的标准方程．

17．设抛物线y²=2px (p>0)上各点到直线3x+4y+12=0的距离的最小值为1，求p的值．

18．直线y=x+b与双曲线2x²－y²=2相交于A, B两点，若以AB为直径的圆过原点，求b的值．

19．已知椭圆的中心在原点，准线为x=±4，若过直线x－y=0与椭圆的交点在x轴上的射影恰为椭圆的焦点，

（1）求椭圆的方程；

（2）求过左焦点F₁且与直线x－y=0平行的弦的长．

20．如图，已知F(0, 1)，直线l: y=－2，圆C: x²+(y－3)²=1，

（1）若动点M到点F的距离比它到直线l的距离小1，求动点M的轨迹E的方程；

（2）过轨迹E上一点P作圆C的切线，当四边形PACB的面积S最小时，求点P的坐标及S的最小值。

参考答案

一．选择题：

题号	1	2	3	4	5	6	7	8	9	10
答案	A	B	C	A	D	D	A	D	B	D

二．解答题：

11．[－, ]　　　　　　　　　  12．x²＋y²±8x＝0

13．　　　　　　　　　　　　  14．(x－1)²＋y²=5

三．解答题

15．设点P(x, y)是轨迹上任意一点，点A的坐标是(x₁, y₁), 点B的坐标是(x₁, 0),

　∵点P分有向线段BA的比λ＝,

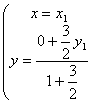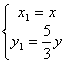　∴ , ∴ ,　又点A在圆x²＋y²＝25上，

　∴ x²＋y²＝25, 即 (y≠0)，

　椭圆的焦点坐标是(－4, 0), (4, 0), 准线方程是x＝±.

16．设所求的方程为(a>b>0), 椭圆上一点为P(x₀, y₀),

　则椭圆的四个顶点分别为(a, 0), (－a, 0), (0, b), (0, －b),

　由已知四直线的斜率乘积为，得＝,

　∵ b²x₀²＋a²y₀²＝a²b², ∴ y₀²＝, x₀²＝,

　代入得＝, 又由已知2ab＝4, 及a>0, b>0, 得a＝2, b＝,

　∴ 椭圆 方程是＝1.

17．设P(x₀, y₀)为抛物线y²=2px上任意一点，则P到直线3x+4y+12=0的距离

  S＝, 将x₀=代入得S=,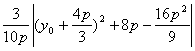

 ∵ S的最小值是1, ∴ 8p－>0(否则若8p－≤0，得S的最小值为0) 且当y₀=－时, =1, 解得p=.