2005-2006学年度第二学期期中练习
高 二 数 学 2005.10.27
一.选择题:
1.设z1=3+4i,z2=-2-i, 那么![]() 是( )。
是( )。
(A)1-3i (B)-2+11i (C)-2+i (D)5-5i
2.抛物线y=2x2的焦点坐标是( )。
(A)(1, 0) (B)(![]() , 0) (C)(0,
, 0) (C)(0, ![]() ) (D)(0,
) (D)(0, ![]() )
)
3.双曲线的焦距等于双曲线的两条准线间距离的2倍,则双曲线的离心率是( )。
(A)![]() (B)
(B)![]() (C)2 (D)3
(C)2 (D)3
4.复数的(![]() )9值等于( )。
)9值等于( )。
(A)![]() (B)
(B)![]() (C)i (D)-i
(C)i (D)-i
5.如果抛物线的顶点在原点,对称轴为x轴,焦点在直线3x-4y-12=0上,则抛物线的方程是( )。
(A)y2=12x (B)y2=-12x (C)y2=16x (D)y2=-16x
6.设z为复数![]() 是z的共轭复数,则z=
是z的共轭复数,则z=![]() 是z为实数的( )。
是z为实数的( )。
(A)充分但不必要条件 (B)必要但不充分条件
(C)充分而且必要条件 (D)既不充分也不必要条件
7.已知等比数列{an}中,a1+a2+a3=18, a2+a3+a4=-9, 记Sn=a1+a2+……+an,则![]() Sn等于( )。
Sn等于( )。
(A)48 (B)32 (C)16 (D)8
8.设正三角形的三个顶点都在抛物线y2=4x上,正三角形的一个顶点是坐标原点,这个正三角形的面积是( )。
(A)48![]() (B)24
(B)24![]() (C)
(C)![]()
![]() (D)46
(D)46![]()
9.过抛物线y2=2x的焦点F的直线与抛物线交于A(x1, y1)、B(x2, y2)两点,若x1+x2=3,则AB等于( )。
(A)2 (B)3 (C)4 (D)5
10.在各项都是正数的等比数列{an}中,公比q≠1,且a2, ![]() a3, a1成等差数列,则
a3, a1成等差数列,则![]() 等于( )。
等于( )。
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
11.设某工厂一月份的产值为a,十月份的产值为4a,假定工厂当年每月的增产值相同,则全年的总产值是( )。
(A)![]() a (B)68a (C)34a (D)17a
a (B)68a (C)34a (D)17a
12..设f (n)=![]() , 则f (n+1)等于
( )
, 则f (n+1)等于
( )
(A)f (n)+![]() (B)f (n)+
(B)f (n)+![]()
(C)f (n)-![]() +
+![]() (D)f (n)+
(D)f (n)+![]() -
-![]()
二.填空题:
13.曲线y2-4y-4x+16=0的焦点坐标为 。
14.设三个实数成等比数列,它们的和为14,它们的积为64,那么这三个数中最大的数是 。
15.设椭圆![]() 上的点P到其左准线的距离是
上的点P到其左准线的距离是![]() ,则点P到其右焦点的距离是
。
,则点P到其右焦点的距离是
。
16.若![]() [2-(
[2-(![]() )n]=2,则实数r的取值范围是
。
)n]=2,则实数r的取值范围是
。
三.解答题:
17.设z是虚数,解方程:![]() +z=2+i.
+z=2+i.
18.直线y=x+b与双曲线2x2-y2=2相交于A、B两点,以A、B为直径的圆恰好通过原点,求b的值。
19.已知{an}是各项都为正实数的数列,若数列{an}的前n项和Sn=![]() (an2+4an+4), 其中an表示通项,n=1, 2, 3, ……,
(an2+4an+4), 其中an表示通项,n=1, 2, 3, ……,
(1)
 试分别求a1, a2, a3的值;
试分别求a1, a2, a3的值;
(2) 试推测an的表达式,并予以证明。
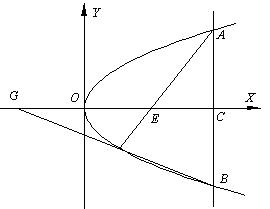
20.已知抛物线y2=2px(p>0), 直线AB垂直于x轴并与抛物线交于A、B两点,其垂足为C(如图),又E是线段OC上一点,G为x轴负半轴上一点,且OE=OG,其中O为坐标原点,求证:直线AE、BG的交点P在抛物线上。
参考答案
一.选择题:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | D | B | D | C | C | C | A | C | A | C | D |
二.填空题:
13.F(4, 2) 14.8
15.6
16.{r r<![]() 或r>1}
或r>1}
三.解答题:
17.z=![]() -i
-i
18.直线y=x+b与双曲线2x2-y2=2相交于A(x1, y1)、B(x2, y2)两点,
联立方程消去y得 x2-2bx-b2-2=0, ∴ x1+x2=2b, x1x2=-b2-2,
由“以A、B为直径的圆恰好通过原点”,可得OA⊥OB,即kOAkOB=-1,
∴ x1x2+y1y2=0, 由y1y2=(x1+b)(x2+b)=2b2-2, ∴ (-b2-2)+(2b2-2)=0,
解得b=±2.
19.(1) a1=2, a2=6, a3=10;
(2) 猜测an=4n-2, 用数学归纳法证明(略)
20.设抛物线y2=2px上A点的坐标为(x0, y0), E点坐标为(m ,0),
则B(x0,
-y0), G(-m, 0), 可得AE的方程为y=![]() ,
,
BG的方程为y=-![]() , 联立解得
, 联立解得 ,
,
∵ yP2=(-![]() )2=
)2=![]() =2p
=2p![]() . ∴ 点P在抛物线上.
. ∴ 点P在抛物线上.