北大附中2002-2003学年第一学期期中考试

数学试卷

2002．11．6

一、选择题：（每个小题3分，共10小题，计30分）在下列各题的四个被选答案中，只有一个是正确的，请你将正确答案前的字母添在答题卡对应的位置。

1、若a、b、c∈R，且a-c<b，则（　 ）

（A）a<b+c　　　　　　  (B)a<b-c

 (C)a<b+c　　　　　　　　  (D)a>c-b

2、已知a>0，b>0，则不等式的解集为（　　）

（A）或　　　　

（B）或

（C）或　

（D）或

3、不等式的解集是（　 ）

（A）（-1，3）　　　　　　　 （B）（-3，1）

（C）（3，+∞）　　　　　　  （D）（-∞，-1）∪（3，+∞）

4、不等式的解集是（　　）

（A）{x x>1}　　　　　　　　 （B）

（C）{x x≥1或x=-2}　　　　 （D）{x x≥-2且x≠1}

5、设，，，则a，b，c的大小关系是（　　）

（A）a<b<c　　　　　　　　　  （B）c<b<a

（C）a<c<b　　　　　　　　　  （D）c<a<b

6、若ab<0，则直线的倾斜角为（　 ）

（A）　　　　　　　　 （B）

（C）　　　　　　　  （D）

7、直线l到直线2x+y-1=0的角是45°，则直线l的斜率是（　 ）

（A）　　　　　　　　　　　  （B）3

（C）-1或3　　　　　　　　　　　 （D）或3

8、下列四个命题中，正确的是（　 ）

（A）通过点（0，2）且倾斜角是15°的直线方程是。

（B）设直线和的斜率分别为和，则和的夹角是。

（C）直线的倾斜角是。

（D）已知三点A（a+b，c），B（b+c，a），C（c+a，b），则A，B，C三点共线。

9、设 k为实数，则直线方程y = k (x+1)表示的图形是（　 ）

（A）通过点（1，0）的一切直线。

（B）通过点（-1，0）的一切直线。

（C）通过点（1，0）且不与y轴平行的一切直线。

（D）通过点（-1，0）且不与y轴平行的一切直线。

10、已知A（3，1），B（-1，2），若∠ACB的平分线在y=x+1上，则AC所在直线方程是（　）

（A）y=2x+1　　　　 　 （B）

（C）y=-3x-1　　　　　  （D）x-2y-1=0

二、填空题：（每空4分，共6空，计24分）请把你认为正确的答案填写在答题卡对应的位置。

11、若不等式的解集是2<x<3，则不等式的解集是：________

12、不等式的解集是：_______________

13、不等式的解集是：_____________

14、函数的定义域是________________，值域是___________。

15、△ABC的顶点坐标分别为A（1，2），B（4，1），C（4，4），直线l平行于BC，截△ABC得到一个小三角形，且截得小三角形面积是△ABC面积的，则直线l的方程为______________

三、解答题：（共6小题，计46分）请写出详细的解题过程。

16、（本题6分）已知，，…，均为正数，且，

求证：

17、（本题8分）已知a，b，，求证：

18、（本题8分）解不等式：

19、（本题8分）解关于x的不等式：

20、（本题8分）求与直线平行，并且与两坐标轴都相交在正半轴所成的三角形面积为24的直线l的方程。

21、（本题8分）等腰三角形两腰所在的直线方程是，

，它的底边所在直线经过点A（3，-8），求底边所在直线方程。

北大附中2002-2003学年第一学期期中考试数学试卷答案

一、选择题答题卡：（每小题3分，共30分）

1A　2B　3C　 4C　 5A　 6C　 7B　　8D　 9D　 10D

二、填空题答题卡：（每个空4分，共24分）

11、　　 

12、（-∞，-1]∪（1，2]

13、，且x≠0

14、；

15、x=2

三、解答题：（共6小题，计46分）请写出详细的解题过程。

16、（本题6分）已知，，…，均为正数，且，

求证：

证明：∵，1>0；

；…………2分

同理：；…………

由不等式性质：上面n大于0的同向不等式相乘，即得：

…………4分

∵已知：，代入上式得：

…………6分

17、（本题8分）已知a，b，，求证：

证明：欲证成立，

只需证明：成立…………2分

即证明：，

∵a，b，…………3分

∴…………6分

可知：成立。

所以，原不等式成立，即…………8分

18、（本题8分）解不等式：

证明：原不等式等价于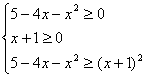　　①…………2分

　　　　　 　　　 或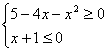　　　　  ②…………4分

由不等式①解得：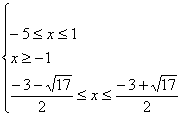

解出：…………6分

由不等式解得：解出：…………7分

综上：原不等式的解集为。…………8分

19、（本题8分）解关于x的不等式：

解：原不等式等价于：

即：（x+a）(x+3)(x+1)>0　　　　  …………3分

①当-a<-3, 即a.>3时：原不等式解集为：（-a,-3）∪（-1，+∞）…………4分

②当-a=-3，即a=3时，原不等式解集为：（-1，+∞）…………5分

③当-3<-a<-1，即1<a<3时，原不等式解集为：（-3，-a）∪（-1，+∞）…………6分

④当-a=-1，即a=1时，原不等式解集为（-3，-1）∪（-1，+∞）…………7分

⑤当-a>-1，即a<1时，原不等式解集为：（-3，-1）∪（-a，+∞）…………8分

20、（本题8分）求与直线平行，并且与两坐标轴都相交在正半轴所成的三角形面积为24的直线l的方程。

解：直线，化为斜截式：

所以，的斜率为；

∵所求直线,

∴l的斜率也为；

∴设l的方程为，…………3分

∵l与两坐标轴都相交在正半轴，∴m>0；

当y=0时，求得直线l和x轴交点为

由已知l与x轴，y轴所围成的三角形面积为24。

所以：，…………6分

解出：m=±6，由分析m>0，舍去-6，所以m=6，…………7分

所以，所求的直线方程为，即：3x+4y-24=0…………8分

解二：设为截距式…………3分

列出方程组…………5分

解出…………7分　 正确答案…………8分

21、（本题8分）等腰三角形两腰所在的直线方程是，，它的底边所在直线经过点A（3，-8），求底边所在直线方程。

解：设，，底边所在直线的斜率分别为，，k；

由得y=7x-9，所以，

由得y=-x+7，所以；…………2分

如图，由等腰三角形性质，可知：l到的角=到l的角；

由到角公式得：…………3分

图　　　　　　　　　  …………4分

解出：k=-3或　　　　 …………6分

由已知：底边经过点A（3，-8），

代入点斜式，得出直线方程：

或………………7分

3x+y-1=0或x-3y-27=0。………………8分