高二数学曲线和方程练习
【同步达纲练习】
A级
一、选择题
1.曲线f(x,y)=0关于直线x-y-2=0时称曲线的方程为( )
A.f(y+2,x)=0 B.f(x-2,y)=0
C.f(y+2,x-2)=0 D.f(y-2,x+2)=0
2.若点M到x轴的距离和它到直线y=8的距离相等,则点M的轨迹方程是( )
A.x=-4 B.x=4 C.y=-4 D.y=4
3.动点P到x轴,y轴的距离之比等于非零常数k,则动点P的轨迹方程是( )
A.y=![]() (x≠0) B.y=kx(x≠0)
(x≠0) B.y=kx(x≠0)
C.y=-![]() (x≠0) D.y=±kx(x≠0)
(x≠0) D.y=±kx(x≠0)
4.方程4x2-y2+4x+2y=0表示的曲线是( )
A.一个点 B.两条互相平行的直线
C.两条互相垂直的直线 D.两条相交但不垂直的直线
5.已知点A(0,-1),点B是抛物线y=2x2+1上的一个动点,则线段AB的中点的轨迹是( )
A.抛物线y=2x2 B.抛物线y=4x2
C.抛物线y=6x2 D.抛物线y=8x2
二、填空题
6.已知A(-1,0),B(2,4),且△ABC的面积是10,则点C的轨迹方程是 .
7.Rt△ABC的斜边AB的长度等于定值C,顶点A、B在x轴,y轴上滑动,则斜边AB的中点M的轨迹方程为
8.到两平行线3x+2y-1=0和6x+4y-3=0的距离相等的点的轨迹方程为 .
三、解答题
9.已知直线l:![]() +
+ ![]() =1,M是直线l上的一个动点,过点M作x轴,y轴的垂线,垂足分别为A、B求把有向线段
=1,M是直线l上的一个动点,过点M作x轴,y轴的垂线,垂足分别为A、B求把有向线段![]() 分成的比λ=2的动点P的轨迹方程.
分成的比λ=2的动点P的轨迹方程.
10.经过点P(3,2)的一条动直线分别交x轴、y轴于点A、B,M是线段AB的中点,连结OM并延长至点N,使|ON|=2|OM|,求点N的轨迹方程.
AA级
一、选择题
1.下列各点中,在曲线x2-xy+2y+1=0上的点是( )
A.(2,-2) B.(4,-3) C.(3,10) D.(-2,5)
2.已知坐标满足方程f(x,y)=0的点都在曲线C上,则( )
A.曲线C上的点的坐标都适合方程f(x,y)=0
B.坐标不适合方程f(x,y)=0的点都不在曲线C上
C.不在曲线C上的点的坐标都不适合方程f(x,y)=0
D.不在曲线C上的点的坐标一定有些适合,也有一些不适合方程f(x,y)=0
3.到两条坐标轴的距离之和等于2的点的轨迹方程是( )
A.x+y=2 B.x+y=±2
C.|x|+|y|=2 D.|x+y|=2
4.到直线l:3x+4y-5=0的距离等于1的点的轨迹方程是( )
A.3x+4y-4=0 B.3x+4y=0或3x+4y-10=0
C.3x+4y+10=0 D.3x+4y-30=0或3x+4y+20=0
5.与A(-1,0)和B(1,0)两点连线的斜率的乘积等于-1的动点P的轨迹方程是( )
A.x2+y2=1 B.x2+y2=1(x≠±1)
C.x2+y2=1(x≠0) D.y=![]()
二、填空题
6.若点P在曲线y=x2+1上,且点P到原点的距离为![]() ,则点P的坐标为 .
,则点P的坐标为 .
7.若两直线x+y=3a,x-y=a的交点在方程x2+y2=1所表示的曲线上,则a= .
8.点P到定点F(4,0)的距离比它到定直线x+5=0的距离小1,则动点P的轨迹方程是 .
三、解答题
9.已知曲线C上的每一点到点A(0,-2)的距离与它到x轴的距离的差等于2,求这条曲线的方程,并画出这条曲线.
10.在△ABC中,AB边的长为2a,若BC边上的中线AD的长为m,试求顶点C的转迹方程.
【素质优化训练】
一、选择题
1.方程(2x+y)(x+y-3)=0与(4x+2y+1)(2x-y+1)=0所表示的两曲线的公共点个数是( )
A.1个 B.2个 C.3个 D.多于3个
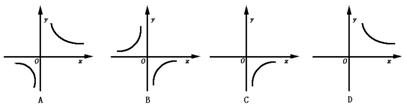
2.方程arccotx+arccoty=π所表示的示意曲线是( )
3.已知△ABC的两个顶点坐标为A(-2,0),B(2,0)第三个顶点C在直线2x-3y+5=0上,则△ABC的重心G的轨迹方程为( )
A.2x-3y+5=0(y≠0) B.6x-9y+5=0(y≠0)
C.6x-3y+5=0(x≠0) D.6x-9y+5=0(x≠0)
4.方程|x|+|y|=1的曲线的周长及其所围成的区域的面积分别为( )
A.2![]() ,1 B.4
,1 B.4![]() ,2 C.6
,2 C.6![]() ,4 D.8,4
,4 D.8,4
5.方程x+y-4![]() +2m=0表示一条直线,则实数m满足( )
+2m=0表示一条直线,则实数m满足( )
A.m=0 B.m=2
C.m=2或m<0 D.m≥2
二、填空题
6.线段AB和CD互相垂直平分于点O,|AB|=2,|CD|=4,动点P满足|PA|·|PB|=|PC|·|PD|,则动点P的轨迹方程为 .
7.点P(x,y)在直线x+2y+1=0上移动,并在函数u=2x+4y取得最小值,则P点坐标为 .
8.已知关于x,y的方程x2-4xy+my2-x+(3m-10)y-2=0表示两条直线,则m= .
三、解答题
9.求两直线l1:x-3my+3=0,l2,3mx+y+9m=0的交点的轨迹,并画出轨迹的图形.
10.设等腰三角形OAB的顶角为2θ,高为h
(1)△OAB内有一动点P到三边OA、OB,AB的距离分别为|PD|、|PF|、|PE|,且满足关系:
|PD|·|PF|=|PE|2,求P点的轨迹.
(2)在上述轨迹中定出P点的坐标,使得|PD|+|PE|=|PF|
【知识探究学习】
如图所示是某防空部队进行射击训练时在平面直角坐标系中的示意图,在地面O、A两个观点测得空中固定目标C的仰角分别为α和β,OA=1千米,tanα=![]() ,tanβ=
,tanβ=![]() ,位于O点正上方
,位于O点正上方![]() 千米的D点处的直升飞机向目标C发射防空导弹,该导弹运行与地面最大高度为3千米,相应水平距离为4千米(即图中E点),不考虑空气阻力,导弹飞行轨道为一抛物线,那么按轨道运行的导弹能否击中目标C?说明理由.
千米的D点处的直升飞机向目标C发射防空导弹,该导弹运行与地面最大高度为3千米,相应水平距离为4千米(即图中E点),不考虑空气阻力,导弹飞行轨道为一抛物线,那么按轨道运行的导弹能否击中目标C?说明理由.
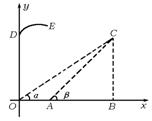
解:能否击中C点,关键是看一下C点是否在导弹飞行的轨迹上,因此应选求C点坐标,然后求轨迹的方程,再验证该点是否满足轨迹方程.
设抛物线为y=a(x-4)2+3,由抛物线过点(0, ![]() ),求得a=-
),求得a=-![]() .
.
所以 y=-![]() (x-4)2+3
(x-4)2+3
=-![]() x2+
x2+![]() x+
x+![]() .
.
设C点坐标为(x0,y0),过C作CB⊥Ox于B,
tanα=![]() =
=![]() ,tanβ=
,tanβ=![]() =
=![]() .
.
则![]() x0=
x0=![]() (x0-1).
(x0-1).
解得x0=7,求出y0=![]() .
.
即C点坐标为(7,![]() ),经计算
),经计算
-![]() x02+
x02+![]() x0+
x0+![]() =-
=-![]() ×72+
×72+![]() ×7+
×7+![]() =
=![]() .
.
所以C点在抛物线上.
故依轨道运行的导弹可以击中目标C.
参考答案:
【同步达纲练习】
A级
1.C 2.D
3.D 4.D 5.B
6.4x-3y+24=0或4x-3y-16=0 7.x2+y2=![]() 8.12x+8y-5=0
9.3x+2y-4=0 10.
8.12x+8y-5=0
9.3x+2y-4=0 10.![]() +
+![]() =1
=1
AA级
1.C 2.C 3.C 4.B 5.B
6.(±1,2)
7.±![]() 8.y2=16x 9.x=0(y>0)或x2=-8y(y≤0) 10.(x+3a)2+y2=4m2
8.y2=16x 9.x=0(y>0)或x2=-8y(y≤0) 10.(x+3a)2+y2=4m2
【素质优化训练】
1.C 2.C 3.B 4.B 5.C
6.2x2-2y2+3=0 7.(- ![]() ,-
,-![]() ) 8.3或4 9.x2+y2=9(x≠0)
) 8.3或4 9.x2+y2=9(x≠0)
10.(1)(x-hsec2θ)2+y2=h2tan2θsec2θ (2)P(![]() ,
,![]() )
)