反正弦函数;反余弦函数

【模拟试题】

  (一)选择题:

　　1. 下列函数中, 存在反函数的是(　　　)

　　A. y=sin x , ( x [0, ]　　　　B. y=sin x , (x)

　　C. y=sin x , ( x)　　　　　  D. y=sin x , (x )

　　2. 下列各式中, 正确的是(　　　)

　　A. 　　　　　　　　 B.

　　C. 　　　　　　　　D.

　　3. 若, 且, 则

　　A. arc sin m　　　B. +arc sin m　　 C. -arc sin m　　　D. arc sin (-m)

　　4. y = sin x　(xR)与y = arcsinx, (x [-1,1])都是(　　  )

　　A. 增函数　　 B. 周期函数　　 C. 奇函数　　 D. 单调函数

　　5. 函数y = arc sin 的单调增区间是(　　  )

　　A. (　B. [-1,1]　C. [0, 1]　D. [-1,0]

  (二) 填空:

　　1. 求值: sin =________________.

　　2. y = arc sin ), 则_______, ________.

　　3. 求值: =________________

　　4. 求值: =_______________

　　5. 函数, 当x =_________时, 函数取得最小值, 最小值是_______; 当x=__________时, 函数取得最大值, 最大值是__________.

  (三) 求满足arc sin (1-a) + arc sin (1－)<0 的a的取值范围.

【试题答案】

  (一)1. D;　提示: 一个函数是否有在反函数是由这个函数的性质决定的, 在某个区间上的单调函数一定在这区间上存在反函数. 由此只要画出各选择分支给出函数的图象, 就可断定本题应选(D)

　　 2. D; 此题涉及到了两种有关反正弦函数的计算. 一种是求反正弦值的正弦值, 另一种是求正弦值的反正弦. 无论是哪一种运算, 都要求对于反正弦函数y=arc sin x 的定义域, 值域掌握准确. 即, 在以上四个选项中, (B)中等号右边的已经超出了的范围. (C)中等号左边的已超出了[－1,1]的范围.

(A)中的也超出了[－1,1]的范围. 故选(D).

　　 3. C. 此题, 并不是反正弦函数定义域的取值范围, 故(A)错误.

　　　　 

　　　　  　故(B)错误.

　　　　  满足条件.

　　　　  而, 故(D)错误. 应选(C).

　　 4. C.正弦函数本身是周期函数, 且单调性不确定. 它不存在反函数, 只有在限定了有变量的取值范围后它才有在反函数, 因此(A). (B). (D)均不对.

　　 5. C. 此函数是复合函数. 且, 则, 当时, . 当时, 故选(C)

  (二)1. ,

　　　　

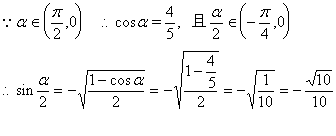
　　　2.

　　　　 　　　 

　　　　

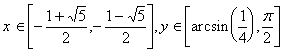
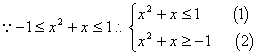
　　 3.

　　　

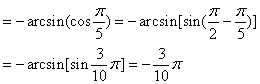
　 4. 若arcsin(sinx)=x, 则必有 而而

　　 5.

　　　　   y有最小值-2, 当, 即时, y有最大值

　　解: