北大附中高二第二学期数学期中考试

______班 姓名：________

　　

　　一、选择题：（30分）

　　1．若用C、R和I分别表示复数集、实数集和纯虚数集，其中C为全集，则

　　A．C=R∪I 　B．R∩I={0}　

　　C．　 D．R∩I=ф

　　2．已知x、y是复数，

　　（1）若，则x=y=0，

　　（2）若xy=0，则x=0或y=0

　　（3），

　　（4）若则x是纯虚数。

　　上面的命题中正确的命题的个数是

　　A．0　B．1　C．2　D．3

　　3．若a>b>0则

　　A．　 B．

　　C．　 D．

　　

　　4．某个命题与自然数n有关，如果当n=k(k∈N)时该命题成立，那么可推出n=k+1时该命题也成立，现已知当n=100时该命题不成立，那么可以推得：

　　A．当n=101时该命题不成立

　　B．当n=101时该命题成立

　　C．当n=99时该命题不成立

　　D．当n=99时该命题成立

　　5．复数等于

　　A．　 B．

　　C．　　D．

　　6．集点在（-1，0），顶点在（1，0）的抛物线方程是

　　A．

　　B．

　　C．

　　D．

　　7．用一个与圆柱母线成60度的平面截圆柱，截口是一个椭圆，这个椭圆的离心率是

　　A．　 B．0.5

　　C．0.25　　D．

　　8．设双曲线C：的左准线与x轴交点是M，则过M与双曲线C有且只有一个交点的直线共有

　　A．2条　B．3条

　　C．4条　D．无数条

　　9．过抛物线的焦点做直线交抛物线与，两点，若则AB等于：

　　A．2p　 B．4p

　　C．6p　　D．8p

　　10．将曲线C向右平移3个单位，再向下平移1个单位得到曲线C′，若曲线C′的方程为，则曲线C的焦点坐标为：

　　A．（6，1），（0，-1）　 B．（-6，1）（0，1）

　　C．（-3，2），（-3，-4）　 D．（3，2），（3，-4）

　　

　　二、填空题：（32分）

　　11．椭圆：的离心率e=_______，准线方程：________.

　　12．复数的实部是______，虚部是______.

　　13．已知等比数列中，，，

　　，则等于_________。

　　14．计算：。

　　15．双曲线中心在原点，对称轴为坐标轴，过，一条渐近线方程为12x-5y=0，则双曲线方程为：___________

　　16．已知方程z-2-z+2=a表示等轴双曲线（实轴和虚轴长度相等的双曲线），则实数a的值为：________

　　17．已知z=2，则当z=_________时，有z+5i的最大值等于___________

　　18．某桥的桥洞是抛物线，桥下水面宽16米，当水面上涨2米后达警戒水位，水面宽变为12米，此时桥洞顶部距水面高度为_________米。（精确到0.1米）

　　

　　三．过程题：

　　19．（6分）求满足下列条件的复数z：

　　20．（8分）过抛物线的焦点，且倾斜角为的直线交抛物线于P、Q两点，O是坐标原点，求△OPQ的面积。

　　21．（12分）已知数列满足：，,　（n∈N）

　　（1）计算、、，猜想数列的通项公式；用数学归纳法给出证明。

　　（2）比较与的大小，证明得到的结论。

　　22．（12分）设双曲线C的中心在原点，对称轴为坐标轴，离心率e=2，其中一个焦点与抛物线相同，直线a：y=kx+1与双曲线C交于A、B两点，

　　（1）求双曲线C 的方程；（2）k 为何值时，以AB为直径的圆过原点；

　　（3）是否存在这样的实数k，使A、B关于直线y=mx对称(m为常数)？若存在求出k；若不存在说明理由。

　　

　　

　　

　　

北大附中高二第二学期数学期中考试参考答案

　　一．1.D 2.B 3.A 4.C 5.D 6.D 7.B 8.C 9.B 10.B

　　二．

　　11．，

　　12．-2，3

　　13．

　　14．-1+(7-9i)/5=-12/5-9i/5

　　15．

　　16．

　　17．2i　7

　　18．2.6

　　

　　三．

　　19．解设z=x+yi,　 x,y∈R

　　

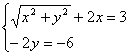
　　解得：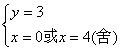

　　所求复数为：z=3i

　　

　　20．解：

　　（1）计算得：、、；(1分)

　　猜想的通项公式为：其中n∈N

　　下面用数学归纳法给出证明：

　　直接验算知，, 满足。

　　假设n=k和n=k+1时猜想成立，即；；

　　

　　

　　猜想也成立，

　　由数学归纳法知：

　　的通项公式是其中n∈N

　　（2），，、、，

　　、、

　　当n≥7有，成立，　 (1分)

　　下面证明这一结论：

　　n=7时已验证命题成立：

　　假设n=k（≥7）时有成立，

　　n=k+1时：，

　　这是因为k≥7时，

　　命题也成立，由数学归纳法知：

　　对n≥7得自然数，有成立。(5分)

　　综上所述：当n=1或n≥7时：；当使：2≤n≤6时，。(6分)

　　

　　21．解：

　　抛物线的焦点为F（1，0），过F点倾斜角为的直线方程设为y=-(x-1)与联立。

　　可以求得PQ=8。坐标原点O到直线y=-(x-1)的距离为△OPQ的高，其数值为，

　　故所求△OPQ的面积为（面积单位）。

　　

　　22．略解：

　　（1）所求双曲线C的方程：

　　（2）……①与直线a：y=kx+1……②联立

　　得：……③

　　△>0得……④

　　设，，要使以AB为直径的圆过原点，就要OA⊥OB，

　　也即：

　　利用③和韦达定理，得，k=±1这个结果也满足条件④。

　　（3）若双曲线C上存在A、B关于直线y=mx对称，则，⑤

　　AB的中点，应在直线y=mx上，

　　于是：

　　……⑥

　　再由③代入⑥：

　　。

　　得到k=3/m这与⑤矛盾。故所求k不存在。