数列
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.
(1)在数列![]() ,
,![]() ,
,![]() ,
,![]() ,…中,如果
,…中,如果![]() 是这个数列中的一项,那么它的项数是( ).
是这个数列中的一项,那么它的项数是( ).
A.6 B.7 C.10 D.11
(2)数列0,2,0,2,…的通项为![]() ,下列公式不能作为已知数列的通项公式的是( ).
,下列公式不能作为已知数列的通项公式的是( ).
A.![]() B.
B.![]()
C.![]() D.
D.![]()
(3)已知数列{![]() }中,
}中,![]() ,
,![]() ,且
,且![]() ,那么
,那么![]() 等于( ).
等于( ).
A.![]() B.21
C.17
D.10
B.21
C.17
D.10
(4)![]() 是数列
是数列![]() 的前n项和,且
的前n项和,且![]() ,那么数列
,那么数列![]() ( ).
( ).
A.是公比为3的等比数列 B.是公差为3的等差数列
C.是公比为![]() 的等比数列 D.既非等差数列也非等比数列
的等比数列 D.既非等差数列也非等比数列
(5)等差数列![]() 中,
中,![]() ,
,![]() ,那么它的前13项和为( ).
,那么它的前13项和为( ).
A.168 B.156 C.78 D.152
(6)等比数列![]() 中,
中,![]() ,且
,且![]() ,则
,则![]() 等于( ).
等于( ).
A.6 B.12 C.18 D.24
(7)数列![]() 中,
中,![]() ,若其前n项和
,若其前n项和![]() ,则n等于( ).
,则n等于( ).
A.9 B.10 C.99 D.100
(8)若a,b,c成等比数列,a,m,b成等差数列,n是b,c的等差中项,则![]() 的值为( ).
的值为( ).
A.4 B.3 C.2 D.1
(9)数列![]() 中,已知
中,已知![]() ,记
,记![]() ,那么
,那么![]() 等于( ).
等于( ).
A.25 B.50 C.100 D.150
(10)等比数列![]() 中,其前n项和为
中,其前n项和为![]() ,且
,且![]() ,
,![]() ,则
,则![]() 的值为( ).
的值为( ).
A.14 B.16 C.18 D.20
(11)在50到350之间的所有个位数字是1的整数的和为( ).
A.5 880 B.5 539 C.5 208 D.4 877
(12)现有200根相同的钢管,把它们堆放成正三角形垛,要使剩余钢管尽可能少,那么剩余钢管的根数为( ).
二、填空题:
(13)![]() 是等差数列
是等差数列![]() 的前n项和,且
的前n项和,且![]() ,
,![]() ,则
,则![]()
![]() =__________.
=__________.
(14)在10到2000之间形如![]() 的各数的和为__________.
的各数的和为__________.
(15)数列![]() 中,
中,![]() ,则此数列的最大项为__________.
,则此数列的最大项为__________.
(16)已知数列![]() 满足
满足![]() ,那么数列
,那么数列![]() 的前n项和的公式为
的前n项和的公式为![]() =__________.
=__________.
三、解答题:
(17)在4与64之间插入三个正数a、b、c,使4,a,b与b,c,64都成等比数列,且使a,b,c成等差数列,求a、b、c的值.
(18)已知等差数列前三项为a,4,3a,前n项和为![]() ,
,![]() .
.
(Ⅰ)求a和k的值;
(Ⅱ)求数列![]() 的前n项和
的前n项和![]() .
.
(19)数列![]() 为正项的等比数列,它的前n项和为80,前2n项和为6 560,且在前n项中数值最大的项为54.求这等比数列的首项
为正项的等比数列,它的前n项和为80,前2n项和为6 560,且在前n项中数值最大的项为54.求这等比数列的首项![]() 与公比q.
与公比q.
(20)已知a 、b 、g 都是锐角,![]() ,且2tanb =tang ,求证:a ,b ,g 成等差数列.
,且2tanb =tang ,求证:a ,b ,g 成等差数列.
(21)在等比数列![]() 中,
中,![]() ,前4项和为45.设
,前4项和为45.设![]() ,试问数列
,试问数列![]() 中有没有最小值?若有,求出这最小项,并指明项数;若没有,说明理由.
中有没有最小值?若有,求出这最小项,并指明项数;若没有,说明理由.
(22)假设A型进口汽车关税税率在2001年是100%,在2006年是25%,2001年A型进口车每辆价格为64万元(其中含32万元关税税款).
(Ⅰ)已知与A型进口车性能相近的B型国产车,2001年每辆价格为46万元.若A型车的价格只受关税降低的影响,为了保证2006年B型车的价格不高于A型车价格的90%,B型车价格要逐年降低,问平均每年至少下降多少万元?
(Ⅱ)某人在2001年将33万元存入银行,假设该银行扣利息税后的年利率为1.8%(五年内不变),且每年按复利计算(例如,第一年的利息计入第二年的本金),那么五年到期时这笔钱连本带息是否一定够买一辆按(Ⅰ)中所述降价后的B型汽车?
参考答案
一、选择题:
(1)B (2)D (3)A (4)D (5)B (6)A
(7)C (8)C (9)B (10)B (11)A (12)B
提示:
(1)给出数列的一个通项公式是![]() .令
.令![]() ,得n=7.
,得n=7.
(3)在已知递推公式中令n=1,可得![]() .再令n=2得
.再令n=2得![]() .
.
(4)![]() 故
故![]() ,当n≥2时,
,当n≥2时,![]() .
.
(5)由已知可求得![]() ,
,![]() .
.
(6)由已知可得![]() .故
.故![]() ,而
,而![]() .
.
(7)![]() ,故
,故![]() .
.
(8)由已知有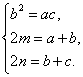 消b得(2m-a)(2n-c)=ac.
消b得(2m-a)(2n-c)=ac.
(9)由![]() .故当n=1,2,3,4,5时
.故当n=1,2,3,4,5时![]() ,n≥6时
,n≥6时![]() .
.
![]() .
.
(10)由![]() 、
、![]() 可得
可得![]() .故
.故![]() ,
,![]() .
.
因此![]()
=![]() .
.
(11)这些数可组成51为首项,341为末项的等差数列,且共有30个数.
(12)n层的正三角钢管垛总共用钢管数为![]() ,这里求使
,这里求使![]() ,
,![]() ,且n尽量大,经估算知n=19.
,且n尽量大,经估算知n=19.
二、填空题:
(13)528 (14)2032
(15)![]() (16)
(16)![]() .
.
提示:
(13)![]() .所求为
.所求为![]() .
.
(14)这些数组成以![]() 为首项,2为公比,共7项的等比数列.
为首项,2为公比,共7项的等比数列.
(15)![]() ,故n=1,2,3时,
,故n=1,2,3时,![]() ;n≥4时,
;n≥4时,![]() .
.
(16)由![]() ,则
,则![]() = (n-1)n(n+1)(n≥2).
= (n-1)n(n+1)(n≥2).
两式相减得![]() ,且
,且![]() .于是
.于是![]() .
.
三、解答题:
(17)设a=b-d、c=b+d.则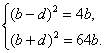 解得d=15.
解得d=15.
代入可得![]() ,故b=25,b=9(舍去).
,故b=25,b=9(舍去).
于是a=10,b=25,c=40.
(18)(1)依题意有3a+a=8,故a=2.于是等差数列前三项为2,4,6,其首项为2,公差为2.
又由![]() ,得
,得![]() .解得k=50.
.解得k=50.
(2)由(1)![]() .
.![]() .
.
∴ ![]() .
.
(19)若q=1,则有![]() 与题意不符,故q≠1.于是依题意有
与题意不符,故q≠1.于是依题意有
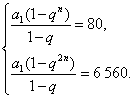 两式相除,并化简可得
两式相除,并化简可得![]() .故
.故![]() 或
或![]() (舍去).
(舍去).
由![]() ,故q>1,所以数列
,故q>1,所以数列![]() 前n项中,
前n项中,![]() 最大,即
最大,即![]() .
.
由![]() ,得
,得![]() ,即
,即![]() .
.
再把![]() 代入
代入![]() 中可得
中可得![]() .
.
由此解得![]() ,q=3.
,q=3.
(20)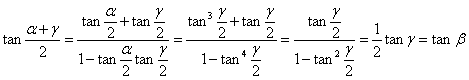 .
.
且a 、b 、g 均为锐角,故![]() ,
,![]() ,于是
,于是![]() ,即a ,b ,g 成等差数列.
,即a ,b ,g 成等差数列.
(21)设等比数列![]() 的公比为q,依题意有
的公比为q,依题意有
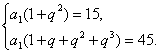 解得
解得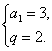
∴ ![]() ,
,![]() ,
,![]() .
.
又![]() ,于是当n=2或3时,
,于是当n=2或3时,![]() 最小,为-12.
最小,为-12.
(22)(Ⅰ)因为2006年关税税款为2001年的![]() ,故所减少的关税税款为
,故所减少的关税税款为![]() (万元).
(万元).
所以2006年A型车价格64-24=40(万元).
因为5年后B型车价格应不高于A型车价格的90%,故B型车价格≤40×90%=36(万元).
又2001年B型车价格为46万元,故5年中至少要降10万元,所以平均每年至少降价2万元.
(Ⅱ)依题意,2001年存入33万元,5年到期时连本带息可得![]() (万元).而
(万元).而![]() >33(1+5×0.018+10×0.000324)=36.07692(万元).
>33(1+5×0.018+10×0.000324)=36.07692(万元).
因此,能买一辆依(Ⅰ)中所述5年后降价为36万元以下的B型车.
