北京市海淀区2005-2006学年度第一学期期中数学试卷
高二数学
2005.11
班级______ 学号______ 姓名______ 总分______
一、选择题:本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.若a<0,b>0,且a+b<0,则下列不等式中成立的是( )
(A)-b<a<b<-a
(B)-b<a<-a<b
(C)a<-b<b<-a
(D)a<-b<-a<b
2.设a、b、c、d∈R,且a>b,c>d则下列一定成立的不等式为( )
(A)a-c<b-d
(B)ac>bd
(C)a-d>b-c
(D)![]()
3.直线![]() 的倾斜角为( )
的倾斜角为( )
(A)150° (B)120° (C)60° (D)-60°
4.x>3是![]() 的( )
的( )
(A)必要不充分条件 (B)充分不必要条件
(C)充要条件 (D)既不充分也不必要条件
5.直线![]() ,
,![]() 互相垂直,则a的值为( )
互相垂直,则a的值为( )
(A)-3 (B)1
(C)0或![]() (D)1或-3
(D)1或-3
6.已知直线![]() 和直线kx-y-1=0,若两直线的夹角为60°,则k的值为( )
和直线kx-y-1=0,若两直线的夹角为60°,则k的值为( )
(A)![]() 或0 (B)
或0 (B)![]() (C)
(C)![]() (D)0
(D)0
7.用一段长为Lm的篱笆围成一个一边靠墙的矩形菜园,菜园的最大面积为( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
8.若![]() ,
,![]() ,且
,且![]() 分别是直线
分别是直线![]() ,
,![]() 的方向向量,则a,b的值分别可以是( )
的方向向量,则a,b的值分别可以是( )
(A)2,1 (B)1,2 (C)-1,2 (D)-2,1
二、填空题:本大题共4个小题,每小题4分,共16分,把答案添在题中横线上。
9.不等式![]() 的解集为_______________。
的解集为_______________。
10.设a为实数,则![]() 与
与![]() 的大小关系为
的大小关系为![]() ___________
___________![]() 。
。
11.函数y=3-x+x+4的最小值为______________________。
12.若点(x,y)在直线3x+4y+25=0上移动,则![]() 的最小值为__________。
的最小值为__________。
三、解答题:本大题共5小题,共44分。解答应写出文字说明,证明过程或演算步骤。
13.(本题满分8分)
解不等式![]() 。
。
14.(本题满分8分)
已知点A(4,5),点B(1,2),点C(12,1),点D(11,6,)求四边形ABCD对角线的交点P的坐标。
15.(本题满分8分)
设a,b,c,d都是实数,且![]() ,
,![]() ,证明ac+bd≤1。
,证明ac+bd≤1。
16.(本题满分10分)
已知过点P(1,4)的直线l在两坐标轴上的截距均为正值,当两截距之和最小时,求直线l的方程。
17.(本题满10分)
某工厂计划用甲,乙两台机器生产A、B两种产品,每种产品都要依次进行甲、乙机器的加工,已知生产一件A产品在甲、 乙机器上加工的时间分别为2小时和3小时,生产一件B产品在甲、乙机器上加工的时间分别为4小时和2小时,甲、乙机器每周可分别工作180小时和150小时,若每件A产品的利润是40元,每件B产品的利润是60元,问此工厂应如何安排生产才能获得最大的利润(即如何确定一周内每种产品生产的数量)。
附加题:(做对者加10分)
设![]() 为奇函数,求a的值,并证明在R上f(x)为增函数。
为奇函数,求a的值,并证明在R上f(x)为增函数。
高二数学期中练习参考答案
一、选择题:
1.C,2.C ,3.B, 4.B,5.D,6.A,7.B,8.A
二、填空题:
9.(-∞,-3)∪(-3,0)∪(1,2);
10.![]() ;
;
11.7;
12.25.
三、解答题
13.原不等式等价于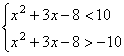 即
即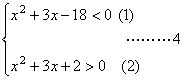 分
分
由(1)解得-6<x<3。由(2)解得x<-2或x>-1…………6分
所以不等式的解集为{x-6<x<-2或-1<x<3}。…………………8分
14.证明:解:设P的坐标为(x,y),则
由B,P,D共线,得![]() 即2x-5y+8=0 (1)………………3分
即2x-5y+8=0 (1)………………3分
由A,P,C共线,得![]() 即x+2y-14=0 (2)………………6分
即x+2y-14=0 (2)………………6分
由(1)(2)解得![]() 所以点P的坐标为(6,4)………………………8分
所以点P的坐标为(6,4)………………………8分
15.证明:因为a,b,c,d都是实数,所以ac+bd≤ac+bd……………3分
![]() …………5分
…………5分
![]() …………8分
…………8分
其它正确解法(见课本第28页)按相应步骤给分。
16.解:设![]() (k<0)l在两轴上的截距分别为a,b…………2分
(k<0)l在两轴上的截距分别为a,b…………2分
则![]() b=4-k,因为k<0,-k>0,
b=4-k,因为k<0,-k>0,![]() ………………………………6分
………………………………6分
![]() …………………………8分
…………………………8分
当且仅当![]() 即k=-2时a+b取得最小值9……………………………………9分
即k=-2时a+b取得最小值9……………………………………9分
所以,所求的直线方程为y-4=-2(x-1),即2x+y-6=0………………………………10分
17.解:设A,B两种产品一周的产量分别为x件,y件,总利润为S,则
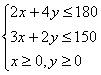 …………3分。
…………3分。
作出可行域(图略)……………………6分
目标函数为S=40x+60y作直线l: 40x+60y=0,把l向右上方移至过
2x+4y=180与3x+2y=150交点,M(30,30)处时,l与原点距离最大。…………8分
此时S=40x+60y取得最大值为3000。 …………9分
因此每天生产A,B产品均为30件时,工厂可获得最在利润3000元。…………10分
附加题:
解:对任意实数x都有![]() ,所以函数的定义域为R。
,所以函数的定义域为R。
因为为奇函数,所以对任意实数均有f(-x)=-f(x)成立。
当x=0时可得f(0)=0,求得![]() ,所以f
,所以f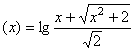 。……3分
。……3分
设![]() 。
。
对于任意实数![]() 当
当![]() 时,
时,
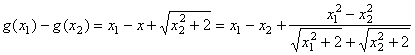 ………………5分
………………5分
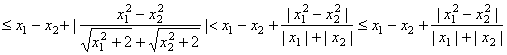
![]() …………………………………………8分
…………………………………………8分
即![]() 因此
因此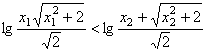 。
。
即![]() 。…………………………………………………………………9分
。…………………………………………………………………9分
所以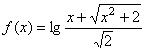 在R上是增函数……………………………………10
在R上是增函数……………………………………10
由于篇幅,其它正确解法按相应步骤给分。
