2005学年第一学期杭州市高二期末教学质量检测数学试题卷

考生须知:

1. 本卷满分100分, 考试时间90分钟.

2. 答题前, 在答题卷密封区内填写学校、班级和姓名.

3. 所有答案必须写在答题卷上, 写在试题卷上无效.

4. 考试结束, 只需上交答题卷.

一．选择题 : 本大题共12小题, 每小题3分, 共36分. 在每小题给出的四个选项中, 有且只有一项是符合题目要求的 .

1．已知直线. 那么直线与的夹角为

 (A) 　　　　　　　(B) 　　　　　 (C) 　　　　　　(D)

2. 若R, 且, 则下列判断正确的是

 (A) 　　　　　　(B) 　　　　　(C) 　　　　　 (D)

3. 若直线经过点, 且倾斜角为, 则直线的方程是

　(A) 　　(B) 　 (C) 　(D)

4. 已知是椭圆的两个焦点, 是椭圆上的点, 若, 则这样的点

　有

　(A) 2个　　　　　  (B) 4个　　　　　  (C) 6个　　　　　 (D) 0个

5. 抛物线的准线方程是

　(A) 　　　　 (B) 　　　　 (C) 　　　　　(D)

6. 已知, 那么之间的大小关系是

　(A) 　(B) 　 (C) 　 (D)

7. 直线和圆的位置关系必定是

 (A) 相离　　　　　 (B) 相交　　　　  (C) 相切　　　　　 (D) 相交或相切

8. 关于的不等式的解集是, 那么另一个关于的不等式的解集应该是

 (A) 　 (B) 　 (C)  (D)

9. 如果, 那么的取值范围是

　(A) 　　　　　　　　　(B)

　(C) 　　　　　　　　　　　　　　　(D)

10. 若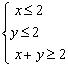, 则线性目标函数的取值范围是

 (A) [ 2,5 ]　　　　 (B) [ 2,6 ]　　　　  (C) [ 3,5 ]　　　　 (D) [ 3,6 ]

11. 已知双曲线 的左, 右焦点分别为, 点在双曲线的右支上, 且, 则此双曲线的离心率的最大值是

　(A) 2　　　　　　　 (B)　　　　　　　  (C)　　　　　　　 (D)

12. 某郊区冬季暖房培植西瓜供应城市市场, 当市场价格上涨时, 市场供给量增加, 市场需求量减少, 具体调查结果如下表:

　　表(1) 市场售价与供给量的关系　　　　　　　 表(2) 市场售价与需求量的关系

单价(元/公斤)	2	2.4	2.8	3.2	3.6	4		单价(元/公斤)	4	3.4	2.9	2.6	2.3	2
供给量(吨)	50	60	70	75	80	90		需求量(吨)	50	60	65	70	75	80

则市场供需平衡 (即供给量和需求量相等时的单价) 所在的一个区间应为

　(A) [2.3, 2.6]　　　 (B) [2.4, 2.6]　　　  (C) [2.6, 2.8]　　　　(D) [2.8, 2.9]

二．填空题：本大题有5小题, 每小题4分, 共20分. 请将答案填写在答题卷中的横线上.

13．椭圆, 双曲线和抛物线, 它们都是 ________________________ 的点的集合(或轨迹).

14. 若, 则有最 ____ 值为 ____ ; 若,则有最 ____ 值为 ____.

15. 若是圆的弦的中点, 那么直线的方程是

　  _____________________ .

16. 已知, 则不等式的解集是 ___________ .

17. 有以下4个命题: ① 若, 则; ② 若, 则;

 ③ 两条直线平行的充要条件是它们的斜率相等; ④ 过点与圆相切的直线方程是. 其中错误命题的序号是

______________ . (把你认为错误的命题序号都填上)

三．解答题：本大题有4小题, 共44分. 解答应写出文字说明, 证明过程或演算步骤.

18．(本小题满分10分)

若不等式  对恒成立, 求实数的取值范围.

19. (本小题满分10分)

设中心在原点的椭圆与双曲线有公共的焦点, 且它们的离心率互为倒数, 求该椭圆的方程.

20. (本小题满分12分)

(理科)圆内有一点(4,2), 过点作直角交圆于, 求动弦中点的轨迹方程.

(文科)直线与圆相交于两个不同的点, 当取不同的实数值时, 求动弦中点的轨迹方程.

21.　(本小题满分12分)

长为(米)的大型机器零件, 在通过传送带的流水线时, 为安全起见, 零件之间的距离不得小于(米). 其中(米/时)是流水线的流速, 为比例系数. 现经测定, 当流速为60 (米/时) 时, 零件之间的安全距离为1.44.

　  (1) 根据给出数据求出比例系数;

(2) 写出流水线上的流量关于流水线流速的函数关系式; (流量是单位时间内通过的零件数, 即)

(3) 应该规定多大的流速, 才能使同一流水线上的零件流量最大? 最大流量是多少?

22 附加题: (本题满分5分, 但全卷总分不超过100分)

课本小结与复习的参考例题中, 给大家分别用“综合法”,“比较法”和“分析法”证明了不等式: 已知都是实数, 且, 则.

这就是著名的柯西(.法国)不等式当时的特例, 即

, 等号当且仅当时成立.

请分别用中文语言和数学语言简洁地叙述柯西不等式, 并用一种方法加以证明.

2005学年第一学期杭州市高二年级教学质量检测

数学参考答案

一．选择题 : 本大题共12小题, 每小题3分, 共36分.

题号12答案ADBACBBDABDC

二．填空题：本大题有5小题, 每小题4分, 共20分.

13．与定点和定直线距离的比是常数 (有道理适当给分)　　　  14.　小, 3; 大, -1　　　　　

15. 　　　　　　　16. 　　　　　　　 17.　② ③ ④.

三．解答题：本大题有4小题, 共44分.

18．(本小题满分10分)

原不等式即为,　　　　　　　　　　　　　　  --- 2分

因其分母二次三项式的判别式恒小于0, 所以分母恒大于0,　　　　　　　  --- 2分

原命题等价于 恒成立, 即

恒成立, 则只需其判别式恒小于0,　　　　　　　　　　　　　　  --- 2分

可解得实数的取值范围为 .　　　　　　　　　　　　　　  --- 4分

19. (本小题满分10分)

由条件可得已知双曲线的半焦距, 离心率,　　　　　　　　　　　　 --- 3分

那么所求的椭圆的半焦距也是, 离心率为, 那么,　　　　  --- 4分

椭圆的半短轴应为, 焦点在轴上, 所求方程应为.　　　　　　  --- 3分

20. (本小题满分12分)

(理)已知圆方程, 设的中点,　　　　　　　 --- 2分

则有,　　　　　　　　　　　　　　  --- 4分

即,　　　　　　　　 　　　　　　--- 2分

整理化简可得中点轨迹方程为.　　　　　　　　　  --- 4分

(文)将直线和圆方程联立, 消去, 得,　　　　　 --- 4分

设此方程两根为, 的中点, 由韦达定理中点坐标得

, 代入直线,　　　　 　　　　　　　　　　　　　　　--- 4分

整理化简可得中点轨迹方程为(位于圆内).　　　　　　 --- 4分

21 (本小题满分12分)

(1) 将流速为60(米/时), 安全距离为1.44代入, 可求得;　　　　　　  --- 3分

(2)　　　　　　　　　　　　　　　--- 3分

(3) , 当, 即流速时, 能使

流量达到最大为.　　　　　　　　　　　　　　  --- 6分

附加题：(满分5分，总分不超过120分)

柯西不等式中文叙述: 两组实数乘积和的平方不大于平方和的乘积;　　　　 --- 1分

数学语言: 给定两组实数，, 则有

.　　　　　　　　　　　　　　  --- 1分

证明: 令,

（1）若全为0，则结论显然成立；

（2）若不全为0，则，为首项系数大于0的一元二次函数，并且，故的判别式

，即,

显然，当且仅当时等号成立.　　　　　　　　　　　 --- 3分

(没有采用求和符号内容过程正确均可以)