6、函数的奇偶性

一、典型例题

1、设f(x)是任意一个函数，且定义域关于原点对称，判断下列函数的奇偶性：

　 ① F(x)=[f(x)+f(－x)]　　　　 ② G(x)= [f(x)－f(－x)]　

2、判断下列函数的奇偶性：

（1）f(x)=　　　　 （2）f(x)=　 (a>0且a≠0)

3、（1）已知函数f(x)的周期为4，且等式f(2+x)=f(2-x)对一切x∈R均成立，求证：f(x)为偶函数。

　（2）设奇函数f(x)的定义域为R，且f(x+4)=f(x),iv x∈[4,6]时，f(x)=2^x+1，求f(x)在区间[－2，0]上的表达式。

4、用定义判断函数f(x)=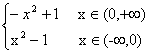　的奇偶性。

5、设函数f(x)的定义域关于原点对称，且对于定义域内任意的x₁≠x₂有f(x₁－x₂)=，

求证：f(x)是奇函数。

6、已知函数 （a>0,a≠1）

（1）试判断函数f(x)的奇偶性；（2）解不等式f(x)≥log_a(2x)。