高中二年级　　班 学号　　  姓名　　　　　  　成绩　　　　　　　

　一．选择题：（每小题5分，共50分）

　1．已知M=arccos(), N= arccos(), P=, 则M、N、P的大小关系是（　）。

　（A）M<P<N　（B）P<M<N  （C）N<P<M  （D）M<N<P

　2．方程=1的解集是（　）。

　（A）{x x=2kπ±, k∈Z}　（B）{x x=2kπ＋, k∈Z}

　（C）{x x=2kπ－, k∈Z}　（D）{x x=kπ±, k∈Z}

　3．已知0<a<1, 则下列不等式正确的是（　）。

　（A）(1－a)<(1－a)　　　 （B）

　（C）　　（D）

　4．若实数m, n, x, y满足m²＋n²=a, x²＋y²=b (a≠b), 则mx＋ny的最大值是 （　）。

　（A）　（B）　（C）　（D）

　5．函数y=(1＋cosx)sin的最大值是（　）。

　（A）　　（B）27　　（C）　 （D）1

　6．△ABC中，a, b, c为三边，A, B, C为内角，且2lgsinB=lgsinA＋lgainC, 那么xsin²A＋ysinA=a和xsin²B＋ysinC=c的位置关系是（　）。

　（A）平行　　（B）重合　　（C）垂直　　（D）相交

　7．已知曲线C₁和C₂的方程分别是F(x, y)=0, G(x, y)=0, 且M(a, b), 那么M(C₁∩C₂)是的（　）。

　（A）充分不必要条件　（B）必要不充分条件

　（C）充要条件　　　　（D）不充分不必要条件

　8．已知P(x₀, y₀)是圆x²＋y²=a²内异于圆心的点，则直线x₀x＋y₀y=a²与此圆的交点的个数是（　）。

　（A）0　　（B）1　　（C）2　　（D）三种情况都可能

　二．填空题：（每小题4分，共20分）

　9．若arccos(3x＋5)≥arccos(2x＋4)成立，则x的取值范围是区间　　　　　 。

　10．设x>0，化简arctgx＋arctg得　　　　　　　　  .

　11．已知函数f (x)=sinx＋5x, x∈(－1, 1),若f (1－a)＋f (1＋a²)<0, 那么a的取值范围是　　　　　　　　  。

　12．关于x的不等式(k²－2k＋)^x<( k²－2k＋)^1－x的解集是{x x<}, 则实数k的取值范围是　　　　　　　　  。

　13．若方程x＋y－6＋3k=0表示一条直线，则实数k的取值范围是　　　　　　　  　。

　14．若直线y=f (x)过点(0, －2), 直线y=g(x)过原点，f[g(x)]=g[f(x)]=3x－2则这两条直线的交点坐标是　　　　　　　　  。

　三．解答题：（16、17题每题7分，18、19题每题8分，共30分）

　15．已知函数y=的最小值是－，最大值是0，其中x满足不等式4^x－1－5·2^x＋16≤0, 求a的值。

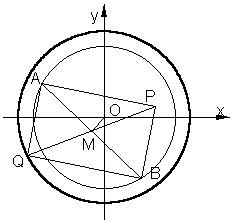
　16．已知圆的方程为x²＋y²=R², 圆内有定点P(a, b)，圆周上有两个动点A、B，使PA⊥PB, 求矩形APBQ的第四个顶点Q的轨迹方程。

　17．已知奇函数f (x)的定义域为实数集，且f (x)在[0, ＋∞),上是增函数，f (0)＝0，当0≤θ≤时,是否存在这样的实数m，使f (cos2θ－3)＋f (4m－2mcosθ)>f (0), 对于所有的θ∈[0,]均成立？若成立，则求出所有适合条件的实数m；若不存在，试说明理由。

参考答案

题号	1	2	3	4	5	6	7	8
答案	B	C	C	D	A	B	B	A

9．[－2, －]　　　　　　　　　  10．

11．1<a<　　　　　　　　  12． k<或k>

13．k≤3　　　　　　　　　　 14．(1, 1)　　 

15．∵ 4^x－1－5·2^x＋16≤0, ∴2^2x－20·2^x＋64≤0, ∴ 4≤2^x≤16, 2≤x≤4

　设t=log_ax,　　 y=,

　则y=(2＋t)(1＋t)≤0且y=(2＋t)(1＋t)=[(t＋)²－]≥－,

　∴ －2≤t≤－1, ∴　－2≤log_ax≤－1, 2≤x≤4,

　当a>1时, log_a4=－1且log_a2=－2, 矛盾，

　当0<a<1时, log_a4=－2且log_a2=－1, ∴ a=.

16．设Q(x, y)为轨迹上任意一点，P(a, b),

A(x₁, y₁), B(x₂, y₂),AB与PQ相交于点M,

则M(),联结OM, 则OM⊥AB,

PQ²=PM²=AM²=OA²－OM²,

∴[(x－a)²＋(y－b)²]=R²－

∴ x²＋y²=2R².

17．奇函数f (x)的定义域为实数集，且f (x)在[0, ＋∞),上是增函数，f (0)＝0，

　∴f (x)在定义域内均为增函数，

　为使f (cos2θ－3)＋f (4m－2mcosθ)>f (0)成立，

　可使f (cos2θ－3)>－f (4m－2mcosθ)= f (2mcosθ－4m),

　即cos2θ－3>2mcosθ－4m, 得cos²θ－mcosθ＋(2m－2)>0

 ∵ 0≤θ≤, ∴ cosθ∈[0, 1]时，cos²θ－mcosθ＋(2m－2)>0均成立，

　当>1, 即m>2时, 只要f(1)>0即可, ∴ f(1)=1－m＋2m－2>0, m>1,

　∴ m>2时cos²θ－mcosθ＋(2m－2)>0均成立，

　当<0, 即m<0时, 只要f(0)>0即可， f(0)=2m－2>0, m>1与m<0矛盾，

　当0≤≤1即0≤m≤2时, 需最小值大于零，

　即>0, 解得2－2<m<2＋2,

　综上所述，当m>2－2时, cos²θ－mcosθ＋(2m－2)>0均成立.