第九章　直线与平面

考试内容：

平面.平面的基本性质.平面图形直观图的画法.

两条直线的位置关系.平行于同一条直线的两条直线互相平行.对应边分别平行的角.异面直线所成的角.两条异面直线互相垂直的概念.异面直线的公垂线及距离.

直线和平面的位置关系.直线和平面平行的判定与性质.直线和平面垂直的判定和性质.点到平面的距离.斜线在平面上的射影，直线和平面所成的角.三垂线定理及其逆定理.

两上平面的位置关系.平行平面的判定和性质.平行平面间的距离.二面角及其平面角.两个平面垂直的判定与性质.

考试要求：

(1)掌握平面的基本性质、空间两条直线、直线和平面、两个平面的位置关系(特别是平行和垂直关系)以及它们所成的角与距离的概念.对于异面直线的距离，只要求会计算已给出公垂线时的距离.

(2)能运用上述概念以及有关两条直线、直线和平面、两个平面平行和垂直关系的性质与判定，进行论证和解决有关问题.

(3)会用斜二测的画法画水平放置的平面图形(特别是正三角形、正四边形、正五边形、正六边形)的直观图.能够画出空间两条直线、两个平面、直线和平面的各种位置关系的图形，能够根据图形想象它们的位置关系.

(4)理解用反证法证明命题的思路，会用反证法证明一些简单的问题.

一、选择题

1.　　　 (85广东)设a、b、c是空间三条直线，下面给出四个命题：
①如果a⊥b，b⊥c，则a∥c；
②如果a、b是异面直线，b、c是异面直线，则a、c也是异面直线；
③如果a与b相交，b与c相交，则a与c也相交；
④如果a与b共面，b与c共面，则a与c也共面.
那么在上述命题中，真命题的个数是
A.4　　　 B.3　　　　C.2　　　　 D.1　　　　　E.0

2.　　　 (86(8)3分)在正方形SG₁G₂G₃中，E，F分别是G₁G₂及G₂G₃的中点，D是EF的中点，现在沿SE，SF及EF把这个正方形折成一个四面体，使G₁，G₂，G₃三点重合，重合后的点记为G，那么，在四面体S－EFG中必有
A.SG⊥△EFG所在平面　　　　　　　　　 B.SD⊥△EFG所在平面
C.GF⊥△SEF所在平面　　　　　　　　　 D.GD⊥△SEF所在平面

3.　　　 (87(4)3分)已知:E，F，G，H为空间中四个点，设命题甲:点E，F，G，H不共面，命题乙:直线EF与GH不相交.那么
A.甲是乙的充分不必要条件　　　　　　　　B.甲是乙的必要不充分条件
C.甲是乙的充要条件　　　　　　　　　　　D.甲是乙的既不充分也不必要条件

4.　　　 (87上海)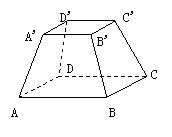在空间中，下述命题正确的是
A.若直线a∥平面M，直线b⊥直线a，则直线b⊥平面M
B.若平面M∥平面N，则平面M内任意一条直线a∥平面N
C.若平面M与平面N的交线为a，平面M内的直线b⊥直线a，则直线b⊥平面N
D.若平面N内的两条直线都平行于平面M，则平面N∥平面M

5.　　　 (88(9)3分)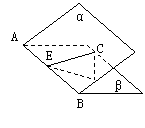如图:正四棱台中，A′D′所在的直线与BB′所在的直线是
A.相交直线　　　　　B.平行直线
C.不垂直的异面直线　D.互相垂直的异面直线

6.　　　 (88(15)3分)

D

如图:二面角α－AB－β的平面角是锐角，C是面α内一点(它不在棱AB上)，点D是点C在面β上的射影，点E是棱AB上满足∠CEB为锐角的任一点，那么
A.∠CEB＞∠DEB　　　B.∠CEB＝∠DEB
C.∠CEB＜∠DEB　　　D.∠CEB与∠DEB的大小关系不能确定

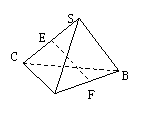
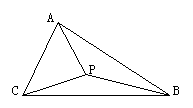
7.　　　 (90(11)3分)如图:正三棱锥S－ABC的侧棱与底面边长相等，如果E，F分别是SC，AB的中点，那么异面直线EF与SA所成的角等于
A.90°　　　　　B.45°　　　　　 C.60°　　　　　D.30°

8.　　　 (90上海)

A

设a、b是两条异面直线，那么下列命题中的假命题是
A.经过直线a有且只有一个平面平行于直线b
B.经过直线a有且只有一个平面垂直于直线b
C.存在分别经过a和b的两个互相平行的平面
D.存在分别经过a和b的两个互相垂直的平面

9.　　　 (90广东)如果直线l是平面α的斜线，那么在平面α内
A.不存在与l平行的直线　　　　　 B.不存在与l垂直的直线
C.与I垂直的直线只有一条　　　　 D.与l平行的直线有无穷多条

10.　  (91(4)3分)如果把两条异面直线看成“一对”，那么六棱锥的棱所在的12条直线中，异面直线共有
A.12对　　　　 B.24对　　　　　 C.36对　　　　　D.48对

11.　  (91(6)3分)如果三棱锥S－ABC的底面是不等边三角形，侧面与底面所成的二面角都相等，且顶点S在底面的射影O在△ABC内，那么O是△ABC的
A.垂心　　　　　　　B.重心　　　　　　 C.外心　　　　　　　D.内心

12.　  (91上海)设直线a在平面M内，则直线M平行于平面N是直线a平行于平面N的
A.充分不必要条件　　B.必要不充分条件　 C.充分必要条件　　D.既不充分又不必要条件

13.　  (92(9)3分)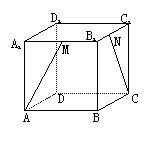在四棱锥的四个侧面中，直角三角形最多可有
A.1个　　　　B.2个　　  C.3个　　　　D.4个

14.　  (92(14)3分)在棱长为1的正方体ABCD－A₁B₁C₁D₁中，M和N分别为A₁B₁和的中点，那么直线AM与CN所成角的余弦值是
A.　　　　B.　　  C.　　　　 D.

15.　  (92上海)在下列条件中，可判定平面α与平面β平行的是
A.α、β都垂直于平面g
B.α内有不共线的三点到β的距离相等
C.l，m是α内两条直线，且l∥β，m∥β
D.l，m是两条异面直线，且l∥α，m∥α，l∥β，m∥β

16.　  (92三南)在长方体ABCD－A′B′C′D′中，如果AB＝BC＝a，AA′＝2a，那么点A到直线A′C的距离等于
A.a　　　　　　B.a　　　　　　C.a　　　　　　 D.a

17.　  (93(18)3分)已知异面直线a与b所成的角为50°，P为空间一点，则过点P且与a，b所成角都是30°的直线有且仅有
A.1条　　　　　　　B.2条　　　　　　　C.3条　　　　　　　 D.4条

18.　  (93上海)设a与b是异面直线，下列命题正确的是
A.有且仅有一条直线与a,b都垂直　　　　 B.有一个平面与a,b都垂直
C.过直线a有且仅有一个平面与b平行　　 D.过空间任意一点必可作一条直线与a,b都相交

19.　  (94(11)5分)对于直线m，n和平面α，β，α⊥β的一个充要条件是
A.m⊥n，m∥α，n∥β　　　　　　　　　 B.m⊥n，α∩β＝m，nÌβ
C.m∥n，n⊥β，mÌα　　　　　　　　　 D.m∥n，m⊥α，n⊥β

20.　  (94上海)在棱长为1的正方体ABCD－A′B′C′D′中，M、N分别为A′B′和BB′的中点，那么AM和CN所成角的余弦值为
A.　　　　　　　B.　　　　　　 C.　　　　　　　　D.

21.　  (94上海)已知a、b是异面直线，直线c平行与直线a，那么c与b
A.肯定是异面直线　　B.肯定是相交直线　 C.不可能是平行直线　D.不可能是相交直线

22.　  (95(10)4分)已知直线l⊥平面α，直线mÌ平面β，有下面四个命题:①α∥βÞl⊥m；②α⊥βÞl∥m；③l∥mÞα⊥β；④l⊥mÞα∥β.其中正确的两个命题是
A.①与②　　　　　　B.③与④　　　　　 C.②与④　　　　　　D.①与③

23.　  (95(15)5分)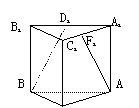

C

如图，A₁B₁C₁－ABC是直三棱柱，∠BCA＝90°，点D₁，F₁分别是A₁B₁，A₁C₁的中点，若BC＝CA＝CC₁，则BD₁与AF₁所成角的余弦值是
A.　　　　 B.0.5　　　　　 C.　　　　　D.

24.　  (96(5)4分)如果直线l、m与平面α、β、γ满足:l＝β∩g，l∥α，mÌα和m⊥g，那么必有
A.α⊥g且l⊥m　　　B.α⊥g且m∥β　　 C.m∥β且l⊥m　　　 D.α∥β且α⊥g

25.　  (96上海)在下列命题中，真命题是
A.若直线m、n都平行于平面α，则m∥n；
B.设α－l－β是直二面角，若直线m⊥l，则m⊥β；
C.若直线m、n在平面α内的射影依次是一个点和一条直线，且m⊥n，则n在α内或n与α平行；
D.设m、n是异面直线，若m与α平行，则n与α相交

26.　  (97(4)4分)已知三棱锥D－ABC的三个侧面与底面全等，且AB＝AC＝，BC＝2，则以BC为棱，以面BCD与面BCA为面的二面角的大小为
A.arccos　　　　B.arccos　　　　 C.　　　　　　　　D.

27.　  (98上海)在下列命题中，假命题是
A.若平面α内的一条直线l垂直于平面β内的任一直线，则α⊥β；
B.若平面α内的任一直线平行于平面β，则α∥β；
C.若平面α⊥平面β，任取直线l∩α，则必有l⊥β；
D.若平面α∥平面β，任取直线l∩α，则必有l∥β

28.　  (2001(9)5分)在正三棱柱ABC—A₁B₁C₁中，若AB＝BB₁，则AB₁与C₁B所成的角的大小为
A．60°　　　　　　 B．90°　　　　　　C．105°　　　　　　D．75°

29.　(2001北京(11)5分)右图是正方体的平面展开图，在这个正方体中，

①BM与ED平行 ②CN与BE是异面直线③CN与BM成角④DM与BN垂直

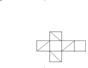以上四个命题中，正确命题的序号是

（A）　　　　　　　　　　　　　　　　　　　　　　　　 ②③　（B）②④  （C）③④　（D）②③④

30．（2001上海（15））若有平面与，且，则下列命题中的假命题为（　　）

A．过点且垂直于的直线平行于．　　　B．过点且垂直于的平面垂直于．
C．过点且垂直于的直线在内．　　　　D．过点且垂直于的直线在内．

二、填空题

1.　　　 (88(20)4分)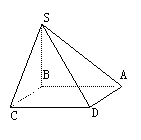如图，四棱锥S－ABCD的底面是边长为1的正方形，侧棱SB垂直于底面，并且SB＝，用α表示∠ASD，则sinα＝__________.

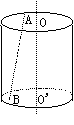
2.　　　 (89(18)4分)如图，已知圆柱的底面半径是3，高是4，A，B两点分别在两底的圆周上，并且AB＝5，那么直线AB与轴OO′之间的距离等于_________.
注:现行考试大纲指出：“对于异面直线的距离，只要求会计算已给出公垂线时的距离”。因此本题考察范围超出大纲要求。

3.　　　 (93上海)正方体ABCD－A′B′C′D′中，过顶点B、D、C′作截面，则二面角B－DC′－C的大小为____________

4.　　　 (96(19)4分)如图，正方形ABCD所在平面与正方形ABEF所在平面成60^o的二面角，则异面直线AD与BF所成的角的余弦值为___________.

5.　　　 (97(19)4分)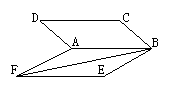已知m，l是直线，α，β是平面，给出下列命题:
①若l垂直于α内的两条相交直线，则l⊥α；
②若l平行于α，则l平行于α内的所有直线；
③若m∩α，l∩β，且l⊥m，则α⊥β；
④若l∩β，且l⊥α，则α⊥β；
⑤若m∩α，l∩β，且α∥β，则m∥l.
其中正确的命题序号是____________(注:把你认为正确的命题的序号都填上)

6.　　　 (99(18)4分)α、β是两个不同的平面，m、n是平面α及β之外的两条不同直线，给出四个论断:①m⊥n，②α⊥β，③n⊥β，④m⊥α.以其中三个论断作为条件，余下一个作为结论，写出你认为正确的一个命题:_________________

三、解答题

1.　　　 (85(13)15分)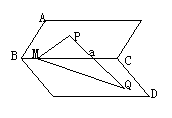如图，设平面AC和BD相交于BC，它们所成的一个二面角为45^o，P为面AC内一点，Q为面BD内一点，圆周直线MQ是直线PQ在平面BD内的射影，并且M在BC中，又设PQ与平面BD所成的角为β，∠CMQ＝θ(0^o＜θ＜90^o＝，线段PM的长为a，求线段PQ的长.

2.　　　 (86(17)10分)如图，AB是圆O的直径，PA垂直于圆O所在的平面，C是圆周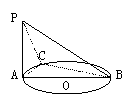上不同于A，B的任意一点，求证:平面PAC⊥平面PBC.

3.　　　 (86上海)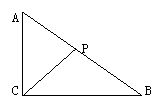Rt△ABC的两直角边长分别为AC＝2,BC＝3，P是斜边BC上一点，沿PC将起折为直二面角A－PC－B，此时AB＝,求二面角P－AC－B的大小

4.　　　 (90(23)8分)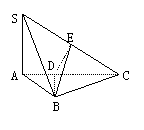如图，在三棱锥S－ABC中，SA⊥底面ABC，AB⊥BC，DE垂直平分SC，且分别交AC、SC于点D、E，又SA＝AB，SB＝BC，求以BD为棱，以BDE与BDC为面的二面角的度数.

5.　　　 (90广东)在三棱锥S－ABC中，SA⊥地面ABC，AB⊥BC，DE垂直平分SC，且分别交AC、SC于点D、E，又SA＝AB＝a，BC＝a(同上题图)，求证：SC⊥面BDE.

6.　　　 (90上海)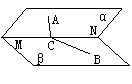如图，平面α、β相交于直线MN，点A在平面α上，点B在平面β上，点C在直线MN上，∠ACM＝∠BCN＝45°.二面角A－MN－B的大小为60°,AC＝1.求：
⑴点A到平面β的距离；
⑵二面角A－BC－M的大小(用反三角函数表示)

7.　　　 (91(23)10分)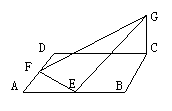已知ABCD是边长为4的正方形，E、F分别是AB、AD的中点，GC垂直于ABCD所在平面，且GC＝2，求点B到平面EFG的距离.

8.　　　 (91上海)如图，设△ABC和△DBC所在的两个平面互相垂直，且AB＝BC＝BD，∠CBA＝∠DBC＝120°，求：
⑴AD的连线与平面BCD所成的角；
⑵AD得连线与直线BC所成的角；
⑶二面角A－BD－C的大小

9.　　　 (92(26)10分)已知:两条异面直线a、b所成的角为θ，它们的公垂线段AA₁的长度为d，在直线a、b上分别取点E、F，设A₁E＝m，AF＝n，求证:EF＝

10.　　已知平面α和不在这个平面内的直线a都垂直于平面β，求证：a∥α(92三南)

11.　　(93上海)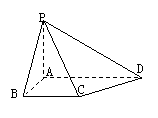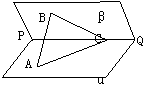如图，已知二面角α－PQ－β为60°，点A和点B分别在平面α和β上，点C在PQ上，∠ACP＝∠BCP＝30°，CA＝CB＝a
⑴求证：AB⊥PQ；
⑵求点B到平面α的距离；
⑶设R是线段CA上一点，直线BR与平面α所成角的大小为45°，求线段CR的长.

12.　　(94上海)如图，在梯形ABCD中，AD∥BC，∠ABC＝90°,AB＝a,AD＝3a,且∠ADC＝arcsin,又PA⊥平面ABCD，PA＝a,求：
⑴二面角P－CD－A的大小(用反三角函数表示)；
⑵点A到平面PBC的距离.

13.　　(96上海)如图，在二面角α－l－β中，A、B∈α，C、D∈l，ABCD为矩形，P∈β，PA⊥α，且PA＝AD，M、N依次是AB、PC的中点
⑴求二面角α－l－β的大小；
⑵求证：MN⊥AB；
⑶求异面直线PA与MN所成角的大小.

14.　  (97上海)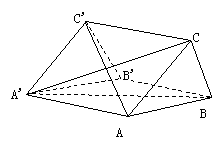如图，在三棱柱ABC－A′B′C′中，四边形A′ABB′为菱形，四边形BCC′B′为矩形，C′B′⊥AB
⑴求证：平面CA′B⊥平面A′AB；
⑵若C′B′＝2，AB＝4，∠ABB′＝60°，求AC′与平面BCC′所成角的大小(用反三角函数表示)

15.　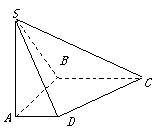  (2001(17)12分)如图，在底面是直角梯形的四棱锥S—ABCD中，∠ABC＝90°，SA⊥面ABCD，SA＝AB＝BC＝1，AD＝．
　　(Ⅰ)求四棱锥S—ABCD的体积；
　　(Ⅱ)求面SCD与面SBA所成的二面角的正切值．

16.　(2001(19)12分) 已知vc是所在平面的一条斜线，点N是V在平面ABC上的射影，且在的高CD上，AB=a，VC与AB之间的距离为h，点。

（Ⅰ）证明是二面角的平面角；（Ⅱ）当时，证明；（Ⅲ）若（<<），求四面体MABC的体积。