高考第一轮复习数学单元测试卷
参数方程、极坐标
第Ⅰ卷（选择题，共60分）
一、 选择题（本大题共12小题，每小题5分，共60分）
1、
曲线的参数方程为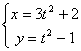
(t是参数)，则曲线是
A、线段 B、双曲线的一支 C、圆 D、射线
2、
极坐标方程
表示的曲线是
A、圆 B、椭圆 C、双曲线的一支 D、抛物线
3、 原点与极点重合，x轴正半轴与极轴重合，则点（-6，-8）的极坐标是
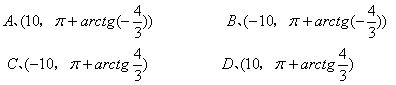
4、 在极坐标系中有如下三个结论：
①点P在曲线C上，则点P的极坐标满足曲线C的极坐标方程；
②
表示同一条曲线；
③ρ=3与ρ=-3表示同一条曲线。
在这三个结论中正确的是：
A、①③ B、① C、②③ D、③
5、
已知动园：
是常数），则圆心的轨迹是
A、直线 B、圆 C、抛物线的一部分 D、椭圆
6、
在参数方程
（t为参数）所表示的曲线上有B、C两点，它们对应的参数值分别为t1、t2，则线段BC的中点M对应的参数值是
7、
的位置关系是
A、相交
B、相切
C、相离
D、视
的大小而定
8、 下列参数方程（t为参数）中与普通方程x2-y=0表示同一曲线的是
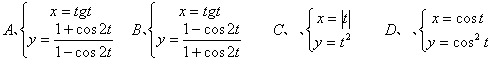
9、
已知点
为
A、正三角形 B、直角三角形 C、锐角等腰三角形 D、直角等腰三角形
10、圆
的圆心的极坐标是
A、
B、
C、
D、
11、直线
的位置关系是
A、平行 B、垂直 C、相交不垂直 D、与
有关，不确定
12、已知过曲线
上一点P原点O的直线PO的倾斜角为
，则P点坐标是
A、（3，4） B、
C、(-3，-4) D、
第Ⅱ卷（非选择题，共90分）
二、 填空题（本大题共4小题，每小题4分，共16分）
13、圆锥曲线
的准线方程是_______________________。
14、在极坐标系中，点P
=1的距离等于____________。
15、过抛物线y2=4x的焦点作倾斜角为的弦，若弦长不超过8，则的取值范围是________________________________。
16、与曲线
对称的曲线的极坐标方程是________________________。
三、 解答题（本大题共6小题，共74分。解答应写出文字说明、证明过程或演算步骤。）
17、（本小题满分10分）
已知方程
。
（1） 试证：不论
如何变化，方程都表示顶点在同一椭圆上的抛物线；
（2） 为和值时，该抛物线在直线x=14上截得的弦最长？并求出此弦长。
18、（本小题满分12分）
在极坐标系中，已知圆C的圆心C(3，
)，半径=1，Q点在圆C上运动。
（1） 求圆C的极坐标方程；
（2） 若P在直线OQ上运动，且OQ∶QP=2∶3，求动点P的轨迹方程。
19、（本小题满分12分）
已知椭圆
上两个相邻顶点为A、C，又B、D为椭圆上的两个动点，且B、D分别在直线AC的两旁，求四边形ABCD面积的最大值。
20、（本小题满分12分）
建立极坐标系证明：已知半圆直径∣AB∣=2（>0），半圆外一条直线
与AB所在直线垂直相交于点T，并且∣AT∣=2
。若半圆上相异两点M、N到的距离∣MP∣，∣NQ∣满足∣MP∣∶∣MA∣=∣NQ∣∶∣NA∣=1，则 ∣MA∣+∣NA∣=∣AB∣。
21、（本小题满分14分）
定弓形弧上有一动点P，连接AP并延长至C，使∣AC∣=2
；连接BP并
延长至D，使∣BD∣=2b，求线段CD中点的轨迹方程。
22、（本小题满分14分）
舰A在舰B的正东，距离6千米；舰C在舰B的北偏西300，距离4千米。它们准备围捕海中的一种动物。某时刻A发现动物信号，4秒后B、C同时发现这种信号。A向动物发射麻醉弹。假设舰与动物都是静止的，动物信号的传播速度为1千米/秒，炮弹初速度为
千米/秒，其中g为重力加速度，空气阻力不计，求舰A炮击的方位角与仰角。
高考数学第一轮复习检测
参数方程、极坐标参考答案
一、 选择题：（每题5分，共60分）
1、D 2、D 3、D 4、D 5、D 6、B
7、B 8、B 9、D 10、A 11、B 12、D
二、 填空题：（每题4分，共16分
13、
14、
15、
16、
三、 解答题（共六个小题，满分74分）
17、（10分）
（1）略 （2）当
时，弦长最大为12。
18、（12分）
（1）
（2）
19、（12分） 
20、（12分）以A为极点，射线AB为极轴建立极坐标系，证明略。
21（14分）
22、（14分）方位角为北偏东300，仰角为300或600。