高二上学期数学期末考试题
班次 ____ 姓名 _____ 计分
一、选择题:本大题共12小题,每小题3分,共36分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知直线的斜率是-1,则它的倾斜角是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.下列说法中正确的是( )
A.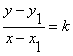 表示过点P(x1,y1)且斜率为k的直线方程
表示过点P(x1,y1)且斜率为k的直线方程
B.直线y=kx+b与y轴交点到原点的距离为b
C.在x轴和y轴上截距分别为a、b的直线方程是![]()
D.方程(x2-x1)(y-y1)=(y2-y1)(x-x1)表示过两点P1(x1,y2),P2(x2,y2)的直线方程
3、直线 L1⊥L2 是 K1·K2=-1 的( )
A、充分而不必要条件 B、必要而不充分条件 C、充要条件 D、既不充分也不必要条件
4、若a>0>b,0<c<d, 则下列不等式中不成立的是( )
(A)ac>bd (B)![]() (C)a+c>b+d
(D)a+d>b+c
(C)a+c>b+d
(D)a+d>b+c
5、若x >0, y >0且![]() = 1, 则x + y的最小值是 ( )
= 1, 则x + y的最小值是 ( )
(A) 6 (B) 12 (C) 16 (D) 24
6、一动点P(x,y)到直线x= -1的距离与它到点(-2,0)的距离的比为![]() ,则P的轨迹为 ( )
,则P的轨迹为 ( )
A)椭圆 B)双曲线 C)抛物线 D)不能确定
7、圆(x-3)2+(y-3)2=9上到直线3x+4y-11=0的距离为1的点有 ( )
A)1个 B)2个 C)3个 D)4个
8、已知椭圆![]() ,F1,F2是它的焦点,AB是过F1的弦,则
,F1,F2是它的焦点,AB是过F1的弦,则![]() ABF2的周长为( )
ABF2的周长为( )
A)![]() B)
B)![]() C)
C)![]() D)
D)![]()
9、已知下列命题:
(1)两直线互相垂直的充要条件是这两直线的斜率的乘积为-1;
(2)过点(-1,1)且斜率为2的直线方程为![]() ;
;
(3)过点M(x0,y0) 与直线Ax+By+C=0(AB≠0)平行的直线方 程是A(x-x0)+B(y-y0)=0;
(4)已知二元二次方程Ax2+Cy2+Dx+Ey+F=0,则A=C≠0是这个方程表示圆的必要非充分条件。其中正确的命题是 ( )
(A)(1)(2) ( B)(3)(4) C)(2)(3) D)(1)(4)
10、直线![]() 与两坐标轴围成三角形的面积是
与两坐标轴围成三角形的面积是![]() ,则t的值是
,则t的值是
11、对任意实数m,直线(m+3)x+(2m-1)y+7=0恒过定点
12、抛物线![]() 上一点M到焦点的距离为a,则点M到y轴的距离为 。
上一点M到焦点的距离为a,则点M到y轴的距离为 。
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题:本大题共6小题,每小题4分,共24分。把答案填在题目中的横线上。
13、若a>b>c>0,那么![]() 四个数从小到大排列的顺序是
四个数从小到大排列的顺序是
14、设a>b>0,则a2+![]() 的最小值是________
的最小值是________
15、某抛物线型拱桥的跨度是20米,拱高4米。在建桥时每隔4米需要一支柱支撑,其中最长的支柱是_____________米
16、过点(-1,1)的所有直线中,与点(2,-1)距离最远的直线方程为 。
17、过点P(3,0)作直线l,使它被两相交直线2x-y-2=0和x+y+3=0所截得的线段中点恰好被P点平分,则直线l的方程是 。
18、一动圆M和直线l:x= —2相切,且经过点F(2,0),则圆心的轨迹方程是
三、解答题:(本大题共6小题,共40分)
19、(本题满分6分)求经过l1∶2x-3y+2=0与l2∶3x-4y-2=0的交点,且分别满足下列条件的直线方程.
(1)过点(1,1); (2)平行于直线2x-y-2=0; (3)垂直于直线4x+3y-1=0.
20. (本题满分7分)已知等腰直角三角形的斜边所在直线方程是:3x-y+2=0,直角顶点C(![]() ),求两条直角边所在的直线方程和此三角形面积.
),求两条直角边所在的直线方程和此三角形面积.
21、(本题满分6分)光线由点P(1,2)射到直线x+y+1=0上,反射后经过点Q(1,-1),求入射光线及反射光线所在的直线方程.
22.(本小题满分7分)已知双曲线的中心在原点,对称轴为坐标轴,且过点A(5![]() ,-12),双曲线的一条渐近线平行于直线12x-5y+35=0,求双曲线的标准方程.
,-12),双曲线的一条渐近线平行于直线12x-5y+35=0,求双曲线的标准方程.
23.(本小题满分7分)已知直线L:y=-x+b和椭圆C:![]() 相交于不同的两点A、B,
相交于不同的两点A、B,
(1) 求b的取值范围;
(2) 当点A、B与原点构成以AB为斜边的直角三角形时,求b的值;
24.(本小题满分7分)已知圆C:(x+4)2+y2=4,圆D的圆心D在y轴上且与圆C外切,圆D与y轴交于A、B两点,点P坐标为(-3,0)。
(1)
若点D坐标为(0,3),求![]() APB的正切值;
APB的正切值;
(2)
当点D在y轴上运动时,求![]() APB的最大值;
APB的最大值;