苏苑中学高二数学期终试卷
命题人:蔡守鸣 班级______姓名_________
一.选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题意要求的。
1.若直线的斜率k= -5,则倾斜角α= ( )
A.arctan(-5) B. π-arctan(-5) C.arctan5 D. π-arctan5
2.直线![]() 在两坐标轴上的截距相等,则
在两坐标轴上的截距相等,则![]() 满足条件是( )
满足条件是( )
A.![]() B.
B.![]() C.
C.![]() 且
且![]() D.
D.![]() 或
或![]() 且
且![]()
3. (1+x)![]() + (1+x)
+ (1+x)![]() +…….+(1+x)
+…….+(1+x)![]() 的展开式中,含x
的展开式中,含x![]() 项的系数为┄┄( )
项的系数为┄┄( )
A.2![]() B.2
B.2![]() C.C
C.C![]() D. C
D. C![]()
4. 在下面四个椭圆中,最接近与圆的是 ( )
A.9x2+y2=36 B.![]() C.
C.![]() D.2x2+y2=8
D.2x2+y2=8
5.甲、乙射击的命中率分别为0.6、0.9,两个独立各射击一次,只有一人命中的概率( )
A.0.38 B.0.42 C.0.54 D.0.96
6.若6人随意排成一排,其中甲、乙、丙恰好相邻的概率为 ┄┄┄( )
A.![]() B.
B. ![]() C.
C. ![]() D.
D.
![]()
7.若过点P(-2,1)作圆(x-3)2+(y+1)2=r2的切线有且仅有一条,则圆的半径r为 ( )
A.29 B. C.小于 D.大于
8.若椭圆![]() 上一点P到右焦点距离为3,则P到左准线的距离为 ( )
上一点P到右焦点距离为3,则P到左准线的距离为 ( )
A.![]() B.
B.![]() C.2
D.4
C.2
D.4
9.从1,2,……,9这九个数中,随机抽取3个不同的数,则这3个数的和为偶数的概率是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
10.点P(-3,1)在椭圆![]() 的左准线上.过点P且方向为a=(2,-5)的光线,经直线y=-2反射后通过椭圆的左焦点,则这个椭圆的离心率为 (
)
的左准线上.过点P且方向为a=(2,-5)的光线,经直线y=-2反射后通过椭圆的左焦点,则这个椭圆的离心率为 (
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.椭圆有这样的光学性质:从椭圆的一个焦点出发的光线,经椭圆反射后,反射光线经过椭圆的另一个焦点. 今有一个水平放置的椭圆形台球盘,点A、B是它的两个焦点,其中焦距为![]() ,长轴长为
,长轴长为![]() ,当放在点A处的小球被击出发,经椭圆壁反弹后再回到点A时,小球经过的路程是 ( )
,当放在点A处的小球被击出发,经椭圆壁反弹后再回到点A时,小球经过的路程是 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.以上答案均有可能
D.以上答案均有可能
12. 将语、数、外、理、化、生六本课外辅导书赠送给希望工程学校的四名学生阅读,每人至少一本,至多两本,恰好有一人同时获得理、化两本书的概率是 ( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
二、填空题:本大题共6小题,每小题4分,共24分.
13. 5人排成一排,其中甲、乙之间至少有一人的排法概率为______ 。
14. 若动点![]() 分别在直线
分别在直线![]() :
:![]() 和
和![]() :
:![]() 上移动,则
上移动,则![]() 中点
中点![]() 到原点距离的最小值为
。
到原点距离的最小值为
。
15. 已知x, y满足约束条件![]()
16.若双曲线的渐近线方程为![]() ,它的一个焦点是
,它的一个焦点是![]() ,则双曲线的方程是__________。
,则双曲线的方程是__________。
17. 对于椭圆![]() 和双曲线
和双曲线![]() 有下列命题:
有下列命题:
①椭圆的焦点恰好是双曲线的顶点; ②双曲线的焦点恰好是椭圆的顶点;
③双曲线与椭圆共焦点; ④椭圆与双曲线有两个顶点相同.
其中正确命题的序号是 .
18.我们知道若AB是椭圆![]() 的不平行于对称轴且不过原点的弦,M为AB的中点,则
的不平行于对称轴且不过原点的弦,M为AB的中点,则![]() .在双曲线中是否也有类似的命题?若有,请写出在双曲线中的一个类似的正确命题:
。
.在双曲线中是否也有类似的命题?若有,请写出在双曲线中的一个类似的正确命题:
。
三、解答题:本大题共5小题,共66分.解答应写出文字说明、证明过程或演算步骤.
19、若某一等差数列的首项为![]() ,公差是
,公差是![]() 的常数项,其中m是
的常数项,其中m是![]() -15除以19的余数,则此数列前多少项的和最大?并求出这个最大值。
-15除以19的余数,则此数列前多少项的和最大?并求出这个最大值。
20、平面上两个质点A、B 分别位于(0,0),(2,2),在某一时刻同时开始,每隔1秒钟向上下左右任一方向移动1个单位,已知质点A向左右移动的概率都是![]() 向上下移动的概率分别是
向上下移动的概率分别是![]() 和
和![]() 质点B向各个方向移动的概率是
质点B向各个方向移动的概率是![]() 求:(1)4秒钟后A到达C(1,1)的概率;(2)三秒钟后,A,B同时到达D(1,2)的概率.
求:(1)4秒钟后A到达C(1,1)的概率;(2)三秒钟后,A,B同时到达D(1,2)的概率.
21.(12分)已知以坐标原点为中心的椭圆,满足条件(1)焦点F1的坐标为 ( 3, 0 );
(2)长半轴长为5.则可求得此椭圆方程为 ![]() (※)问可用其他什么条件代替条件(2),使所求得的椭圆方程仍为(※)?请写出两种替代条件,并说明理由。
(※)问可用其他什么条件代替条件(2),使所求得的椭圆方程仍为(※)?请写出两种替代条件,并说明理由。
22.(14分)已知椭圆的一个焦点F1(0,![]() ),对应的准线方程为y=
),对应的准线方程为y=![]() ,且一个顶点的坐标为(0,3)。
,且一个顶点的坐标为(0,3)。
(1)求椭圆方程。
(2)是否存在直线l,使l与椭圆交于不同的两点M、N,且线段MN恰被直线x=![]() 平分;若存在求出l的倾斜角的范围,若不存在,请说明理由。
平分;若存在求出l的倾斜角的范围,若不存在,请说明理由。
23.(14分)已知定点![]() ,
,![]() 动点
动点![]() 在
在![]() 轴上运动,过点
轴上运动,过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,并延长
,并延长![]() 到点
到点![]() ,且
,且![]() ,
,![]() 。
。
①求动点![]() 的轨迹方程;
的轨迹方程;
②直线![]() 与动点
与动点![]() 的轨迹交于
的轨迹交于![]() 两点,若
两点,若![]() ,且
,且![]() ,求直线
,求直线![]() 的斜率的取值范围。
的斜率的取值范围。
苏苑高级中学2005-2006学年度第一学期
高二数学期末测试答案
一、选择题
DDDBB,ABCCA,DA
二、填空题
13.![]() 14.3
14.3![]() ,15.1,16.
,15.1,16.![]() ,17.①②,18.
,17.①②,18.![]()
三、解答题
19、解:由![]()
![]() 所以n=2
所以n=2
故a1=![]() =100
=100
又7777-15=(76+1)77-15=76M-14=19(4M-1)+5
故 m=5,
![]() 的常数项为
的常数项为![]()
所以 公差d=-4
![]()
当n=25或n=26时 Sn有最大值1300。
20、(1)4秒时,A到达C处,
A在4秒内的运动可以是一次向上且一次向左且两次向右
或者一次向右且一次向下且两次向上
概率为P=P1+P2=![]()
(2)3秒时 A到达D的概率为
21.① 短半轴长为4;
② 离心率 e = ![]() ;
;
③ 右准线方程为 x = ![]() ;
;
④ 点P ( 3, ![]() ) 在椭圆上;
) 在椭圆上;
⑤ 椭圆上两点间的最大距离为10;
……
(答案是开放的,还可写出多种替换条件.)
22.(1)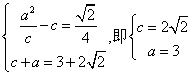 .
.
可得椭圆的方程:![]()
(2)令l:y=kx+m,代入椭圆方程得:(k2+9)x2+2kmx+m2-9=0
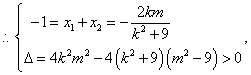 解得
解得![]() .
.
∴倾斜角![]() 。
。
23、解 (1)设动点![]() 的的坐标为
的的坐标为![]() ,则
,则![]() ,
,
![]() ,由
,由![]() 得,
得,![]() ,
,
因此,动点![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]() . …………5分
. …………5分
(2)设直线![]() 的方程为
的方程为![]() ,
,![]() 与抛物线交于点
与抛物线交于点![]() ,则由
,则由![]() ,得
,得![]() ,又
,又![]() ,故
,故![]() .
.
又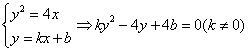 ,
,
∴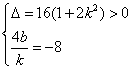 ,
,![]() ,
,
∴![]() 即
即![]()
解得直线![]() 的斜率
的斜率![]() 的取值范围是
的取值范围是![]() . ……………………12分
. ……………………12分