高二暑期数学综合训练题-高中二年级数学试题练习、期中期末试卷、测验题、复习资料-高中数学试卷-试卷试题下载

高二暑期数学综合训练题

各位同学，紧张且具挑战的高三生活还有一个月就要开始了。数学历来是我校教学中的强项，这与各位同学始终如一的热爱数学，在数学这一科花了大量的学习时间是分不开的。为了更好地迎接即将到来的高三数学复习，同时也为了更好地提早发现自己在整个两年的数学学习中存在的问题，请认真解决下列提供的数学问题。

第一卷

(1)集合{a, b, c}的真子集个数为

　 (A)8　　　 (B)7　　　 (C)6　　 (D)5

(2)下面集合M和集合N相等的是

　 (A)M=Æ，N={0}　　　　　　　　　 (B)M={(0, 1)}，N={0, 1}

　 (C)M={5n-1nÎZ}，N={5n+4nÎZ }　　(D)M={y y = x – 1 }，N={(x, y) y = x – 1 }

(3)设全集U={2，3，a²+2a-3}，A={a+1，2}，C_UA={5}，则a的值是

　 (A)2　　　　　 (B) -3或1　　　 (C ) - 4　　　(D) - 4或2

(4)设集合M={xx £}, m=2, 那么下面的关系中正确的是

　 (A)mÏM　　 (B){m}ÎM　　 (C)m　 M　　(D){m}　　M

(5)若M, N是非空集合，U是全集，且M　 N　 U，那么下列集合中，是空集的是

　 (A)M Ç N　　 (B)( C_U M) Ç N　　　(C)M Ç (C_U N)　　 (D) (C_U M) Ç (C_U N)

(6)A={x-2<x<-1或x>1}，B={xx²+px+q£0}，且AÇB={x1<x£3}，AÈB={xx>-2}, 那么

　 (A)p=2，q= -3　　(B)p= -2，q= -3　　(C)p= -4，q=3　　(D)p= -1，q= -6

(7)设A={x1<x<2}，B={xx<a}，若A　 B，则a的取值范围是

　 (A){a a ³ 2}　　(B){a a £ 1}　 (C ) {a a ³ 1}　　 (D){a a £ 2}

(8)若集合A={1, 3, x},B={x², 1},且AÈB={1, 3, x},满足条件的实数x的个数有

　 (A)1个　　　　 (B)2个　　　　 (C )3个　　　　 (D)4个

(9)设全集U=R，集合A={x - 2<x< }, B={xx£ - 2 }, 那么集合C={xx³}等于

　 (A)( C_U A) Ç B　　 (B) (C_U A) È B　　 (C ) (C_U A) Ç (C_U B)　　(D) (C_U A ) È (C_U B)

(10)已知集合M={mmÎN^*且5 - mÎN^*}, 则M的子集的个数为

(A)4　　　　　 (B)16　　　　(C )15　　　 (D)32

(11)设全集U，集合M，N，P满足M Í N, (C_U P) Í (C_U N)，则下列结论中正确的是

　 (A)( C_U M) Í( C_U P)　　　　　　　 (B) (C_U P) Í (C_U M)　　

(12) 适合条件{1}Í A 　{1,2,3,4,5}的集合A的个数是

(A)16　　　　　 (B)15　　　　(C )32　　　 (D)31

(13) 已知f(x)=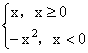，g(x) = 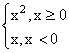, 那么x<0时，则g[f ( x )]等于

　 (A) – x　　　　(B) – x²　　 (C) x　　　　(D) x²

(14) 已知函数f(x)定义域为R，则f(0) = 0是函数f(x)为奇函数的

　 (A) 充分非必要条件　　　　 (B) 必要非充分条件

(15) 设全集U={ xx£ 9且xÎN*}，且(C_UA) Ç ( C_UB) = {1, 3, 7, 9}，则AÈB等于

　 (A){2, 4, 5, 6, 8}　　　(B){1, 3, 7, 9}　　 (C){1, 2, 3 , 4, 5, 6, }　　 (D){2, 4, 6, 8}

(16) 函数y= x²– 2x + 3

　 (A)在[0, 3上既有最小值也有最大值　　 (B)在[0, +¥上既有最小值又有最大值

　 (C)在(0, 3)上既无最小值也无最大值　　 (D)在(0, 3上既有最小值也有最大值

(17) f(x)为奇函数，当x >0时，f(x) = x(1– x )，则当x<0时，f(x)的解析式为

　 (A) x (x – 1 )　 (B) x (1– x )　　 (C) x (x+1)　　 (D) –x (x+1)

(18) 下列各组函数表示同一函数的是

　 (A)y=与y=　　　 (B)y=(与y=x

　 (C)y=与y=　　　 (D)y=与y = x

(19) 函数y= (x>1)的反函数为

　 (A)y = x²+1　　 (B)y = x²+1(x>0)　　 (C)y = x²+1(x<0)　　(D)y = -x²+1(x<0)

(20) 方程x² – 2ax + a +6 = 0的两个实数根分别为x₁, x₂, 则代数式(x₁ –1)² + (x₂ – 1)²的取值范围是

　 (A)[8, +¥]　　　 (B)(8, +¥)　　　 (C)(-¥, -2)È[3, +¥]　　 (D)R

(21) 函数y=x+2+1-x+x在下列区间上为增函数的是

　 (A)(-¥, -2)　　 (B)(-2, 0)　　 (C)[0, +¥ 　　 (D)(-2, +¥)

(22) 已知函数y = f(x)的定义域为[-2 , 4]，则函数y = f(2x – 1 ) +f(1 – 2x)的定义域为

　 (A)[, 2]　　　(B)[, ]　　　(C)[, ]　 (D)[, ]

(23) 若函数y=f(x)的图象经过点(1, 2),其反函数为f^-1(x)，则函数f^-1(2x)的图象一定经过点

　 (A)(1, 2)　　　(B)(2, 1)　　　(C)(1, 1)　　　(D)(0.5, 1)

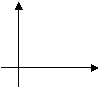
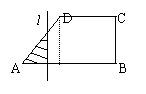(24) 如图，四边形ABCD为直角梯形，上底CD为下底AB的

一半，直线l与AB垂直，截这个梯形所得的位于此直线左方

的图形的面积为y，点A到直线l的距离为x，则函数y = f(x)

的图象大致为

　　y　　　　　　　　 y　　　　　　　　 y　　　　　　　　 y

　　　　　　　　 x　　　　　　　　 x　　　　　　　　 x　　　　　　　　 x

(A)　　　　　　　 (B)　　　　　　　 (C)　　　　　　　 (D)

(25)已知集合A={1, 2, 3}，则满足AÈB=A的集合B的个数有

　 (A)1　　　 (B)7　　 (C)8　　 (D)10

(26)函数y= -x²+4x-2,　xÎ[1, 4]的最小值为

　 (A) –7　　 (B) – 4　　(C) –2　　 (D)2

(27)若不等式ax²+bx+2<0的解集为(-¥, )È(, +¥)，则等于

　 (A)　　 (B)　　 (C) -　　 (D) -

(28)可化简为

　 (A) 　　(B) 　　(C) 　　 (D)

(29)已知函数f(x)=ax⁵-bx³+x²-2，且f(-2)=5，则f(2)等于

　 (A)-5　　 (B)-1　　 (C)1　　　 (D)9

(30)方程log ₂(x²- x) =1的解集是M, 方程2^{2 x+2} – 9 ×2 ^x+4=0的解集为P，那么集合M与集合P的关系是

　 (A)M=P　　 (B)PÌM　　　(C)MÌP　　 (D)MÇP=Æ

(31)从集合{3, 4}到集合{5, 6, 7}可以建立不同的映射的个数为

　 (A)3　　 (B)6　　 (C)8　　 (D)9

(32)若函数y =f(x)是定义在R上的减函数，则函数y= f(x²-2x-3)的单调递增区间为

　 (A)(-¥, -1)　　 (B)(-¥, 1)　　 (C)[1, +¥]　 (D)[-4, +¥]

(33)已知函数f(x)存在反函数f^-1(x)，且f(x+1)=3x-2，则f ^-1(x+1)等于

　 (A)3x-2　　 (B)　　(C)　　(D)

(34)对于定义域是R的任意奇函数f(x)，都有

　 (A)f(x) -f(-x)>0　 (B)f(x) -f(-x)£0　 (C)f(x) ×f(-x) £0　 (D)f(x)× f(-x)³0

(35)已知函数f(x) = log_ax+1 在 (-1, 0)上有f(x)>0，则f(x)

(A)在(-¥, 0)上是增函数　　　 (B)在(-¥, 0)上是减函数

(C)在(-¥, -1)上是增函数　　　(D)在(-¥, -1)上是减函数

(36)已知0<a<b<c，且 lg a > lg c > lg b ，则下列结论一定正确的是

　 (A)(a - 1)(c - 1)>0　 (B)ac>1　 (C)ac<1　 (D)ac=1

(37) 已知“p或q”为真，“p且q”为假，“非p”为真，则必有

(A) p真，q假　　　　　　 (B) p假，q真　

(38)已知f（x）＝，f（a）＝２，则f（－a）等于

　　(A)2　　　　　 (B) - 2　　　　 (C)　　　　　 (D)

(39)在等差数列{a_n}中,a₁+a₄+a₇=39,a₂+a₅+a₈=33,则a₃+a₆+a₉等于

(A) 30　　　　 (B)　27　　　　 (C) 24　　　　　 (D) 21

(40)在等差数列{a_n}中，S₁₀=4S₅, 则等于

(A)　　　　 (B)2　　　　 (C)　　　　(D)4

(41)一个教室的面积为x平方米 , 其窗子的面积为y 平方米, x > y, 如果把称为这个教室的亮度, 现在教室和窗子同时增加m 平方米, 则其亮度将

(A) 增加　　　 (B) 减小　　　 (C) 不变　　　 (D) 不确定

(42)已知各项为正数的等比数列{a_n}公比q¹1, 且a₄, a₆, a₇成等差数列，则等于

　 (A) 　　　　(B) 　　　(C) 2　　　　 (D)

(43)函数y=f (x) 在(0,2)上是减函数,且关于x的函数y=f (x+2)是偶函数,那么有

(A)　f ()<f ()<f (3)　　　　(B)　f (3)<f ()<f ()　　

(44)若函数f(x)=a^x(a＞0,a≠1)为增函数，那么g(x)=log的图象是

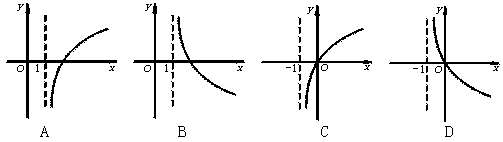
(45)已知{a _n}是等比数列，且a _n>0，a₂a₄ +2a₃ a₅+a ₄a₆ = 25, 那么a₃ +a ₅的值等于

　 (A)5　　　　　(B)10　　　　 (C) 15　　　　 (D)20

(46)《中华人民共和国个人所得税法》规定：公民全月工资、薪金所得不超过800元部分不必纳税，超过800元的部分为全月应纳税所得额，此项税款按下表分段累进计算：

全月应纳税所得额	税率
不超过500元部分	5%
超过500元至2000元部分	10%
超过2000元至5000元部分	15%
．．．　．．．	．．．

某人一月份应纳此项税款26.78元，则他的当月工资、薪金所得介于

(A)800元~900元　　　　　 (B)900元~1200元　　　

(47)定义：函数y＝f（x），x∈Ｄ，若存在常数ｃ，对于任意x_１∈Ｄ，存在唯一的x₂∈Ｄ，使＝ｃ，则称函数f（x）在Ｄ上的均值为ｃ.已知f（x）＝lgx，x∈[10，100]，则函数f（x）＝lgx在[10，100]上的均值为

(Ａ)　　　　　(Ｂ) 　　　　　(Ｃ)　　　　 (Ｄ)10

(48)在某两个正数x, y之间，若插入一个正数a，使x, a, y成等比数列，若另插入两个数b, c，使x, b, c, y成等差数列，则关于t的一元二次方程b×t² – 2a t + c = 0 (b ¹ 0), 则

　　(A)有两个相等的实数根　　　 (B) 有两个相异的实数根

　　(C)无实数根　　　　　　　　 (D) 有两个相等的实数根或无实数根

(49) 已知下列各角：①;　② -240^°;　③180^°;　④495^°，其中是第二象限角的有

　　　　A . 1个　　　 B. 2个　　　C. 3个　　 D. 4个

(50) 终边在第二、四象限的角平分线上的角的集合是

　　　　A.{aa=2kp+, kÎZ}　　　B.{aa=2kp -, kÎZ}

C.{aa=kp+, kÎZ}　　　　D.{aa=kp-, kÎZ}

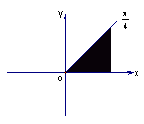
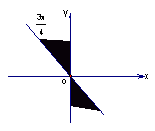
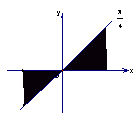
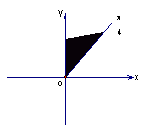(51) 如果sinα+cosα=(≤a≤1)且│sinα│≤│c osα│，那么角α的终边所在的位置(用图中阴影表示)可能是

　　　　 A　　　　　　　　　　　　　　　　　　　 B

　　　　 C　　　　　　　　　　　　　　　　　　　 D

(52) 等于

　　A. sin2 – cos2　　 B. cos2 – sin2　　 C. ±(sin2 – cos2)　　 D. sin2+cos2

(53) 已知函数y=f(x)的图像是C₁，C₁关于y轴对称的图像是C₂，若C₂关于原点对称的图像所表示的函数是y=g(x)，那么g(x)的表达式是

A. g(x) = f(x)　　　　　　 B. g(x) = -f(x)

C. g(x) = f(-x)　　　　　　 D. g(x) = -f(-x)

(54) 若集合A={x∣x=,nÎZ}, 则集合A的元素个数为

　　A. 4个　　　 B. 5个　　　 C. 6个　　　　D.无数个

(55) 已知a、b是第二象限角，且cosa > cosb, 那么下列结论成立的是

A.a < b 　 B. sina > sinb　　C. tana > tanb 　 D. cota < cotb

(56) 已知{a_n}是等差数列，则下列不等式中正确的是

　　A. a₃a₆＜a₄a₅　　 B. a₃a₆≤a₄a₅ 　 C. a₃a₆＞a₄a₅　　D. a₃a₆≥a₄a₅

(57) 已知等比数列的公比是q=2，前4项之和为1，则它的前8项之和为

　　 A. 9 　　　 B. 15　　　　 C. 17 　　　 D. 19

(58) 若定义在R上的奇函数y = f(x)满足：对一切xÎR，都有f(x-2)=f(x+2)，则f(2002)等于

　　A. 0　　　　 B. 4　　　　C. -4　　　　D. 2

(59) 关于x的方程sin²x = , 以下四个结论：

　①它的解集为{x∣x=2kp±,kÎZ}; ②它的解集为{x∣x=kp+,kÎZ};

③它的解集为{x∣x=kp±,kÎZ};　④它的解集为{x∣x=+,kÎZ}.

其中正确的结论是

A.①②　　　　B.③④　　　 C.①②③　　　　D.仅是③

(60) 在三角形ABC中，若sin2A = sin2B, 则三角形ABC必是

　　A. 直角三角形　　　　 B. 等腰三角形　　　

C. 等腰直角三角形　　 D. 等腰三角形或直角三角形

(61)　coscos-sinsin的值是

(A) 　　　　(B) 　　　 (C) 　　　　(D)

(62) 对函数f(x)=ax²+bx+c(a≠0),作x=h(t)的代换，则总不改变函数f(x)值域的代换是

　　 (A) h(t)=10 ^t　　　　　　　(B) h(t)=t²　　

(63) 已知tanx =, tan(x – y) = , 则tan(y – 2x)的值是

(A)　　　　(B)　　　　　(C) 　　　　　(D)

(64) 设是第二象限的角，且则的值是

(A)　　　　　　　　(B)　　　　　(C)-　　　 (D)-

(65) 把函数y＝sin(2x＋)的图象向左平移，所得图象的函数解析式为

(A) y＝sin(2x＋)　　　　　　　(B) y＝sin2x

(66) 在三角形ABC中，已知sinA = cosBcosC, 则下列代数式的值一定为常数的是

　 (A) sinB+sinC　　　 (B)cosB+cosC　　　 (C)tanB+tanC　　　 (D)cotB+cotC

(67) 函数y＝f (x)的图象上每个点的纵坐标保持不变，将横坐标伸长到原来的两倍，然后再将整个图象沿x轴向左平移个单位，得到的曲线与y＝sinx的图象相同，则y＝f (x)的函数表达式是

(A) y＝sin(x－)　　　　　　　(B) y＝sin(2x＋)　

(68) 函数的定义域是

(A){x∣} 　 (B){x∣}

(C){x∣}　　　(D){x∣

(69) (1+tan70^°)(1 – tan25^°)的值等于

(A) 　　　　　　(B) 2　　　　　 (C) 1　　　　　 (D)

(70) 使f (x)＝sin(2x＋)＋为奇函数，且在闭区间[0，]上是减函数的的一个值是

(A)　　　　　 (B) 　　　　 (C) 　　　　(D)

(71) 设f(x)＝xtanx,若,且f(x₁)<f(x₂),则下列结论中，一定成立的是

　　(A)x₁>x₂　　　 (B)x₁+x₂>0　　　　 (C) x₁<x₂　　　　(D) x₁²<x₂²

(72) 若0< a< b < , a = sina + cosa ,　b = cosb - sin b, 则

　　(A) a > b　　　　(B) a < b　　　　(C) ab > 1　　　 (D) ab > 2

(73) 满足f(π+x) = - f(x)，f(-x)=f(x)的函数f(x)可以是

A.cos2x　　　　　B.sinx　　　　　　 C.sin　　　　　　　　 D.cosx

(74) 函数y=½cos²x – sin²x½的最小正周期是

A.　　　　B.π　　　　C. 　　　　 D.2π

(75)设A、B、C是△ABC的三个内角，且tanA、tanB是方程3x²-5x+1=0的两个实根，那么△ABC是

A.钝角三角形　　　　　　　　　　　　　　　　　　　　　　　　B.锐角三角形

C.等腰直角三角形　　　　　　　　　　　　　　　　　　　　　D.等边三角形

(76) 已知函数y=sin(ｘ＋θ)cos(ｘ＋θ)在x=2时有最大值，则θ的一个值是

A. 　　　　　 B. 　　　　　　　　 C. 　　　　　　　　　D.

(77) 若 cosx = ,, 那么sin的值为　　

　　A.　　　　B. 　　　 C.　　　　D.

(78) 若Î，则不等式的解集是

　　　 A．　　　　　　　　　　B．

　　　 C．　　　　　　　　　　　 D．

(79) .函数y=tgx·cosx(0≤x＜，且x≠的图象是

(80) 已知函数f₁(x)=sin(－x), f₂(x)=sinxcosx,　f₃(x)=－arccosx,　f₄(x)=tanx,　从中任取两个相乘得若干个函数，其中偶函数的个数为

A.2　　　　　 B.3　　　　　 C.4　　　　　　 D.6

(81) 若sinx = a (-1 < a <0), 且p < x < , 则x的值为

　　A. arcsina　　　　 B. p - arcsina　　　　C. p+arcsina　　　 D.2p - arcsina

(82) 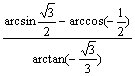的值为

　　　A．2　　　　 B. –3　　　　 C. – 4　　　　 D. – 5

(83) 设ｗ∈R⁺，如果y＝2sinwx在［－，］上单调递增，那么ｗ的取值范围是

A.　　　　　B.　　　　　 C.　　　　 D.

(84) 已知函数f(x) = cos2x +sin(), 下列结论正确的是

　 (A) f(x)是仅有最小值的奇函数　　　　　　　 (B) f(x)是仅有最大值的偶函数

(85)

如图，O为正六边形ABCDEF的中心，则

　等于

(A) 　　　　 (B) 　　　

(86) 若x = 130°, 则下列等式不正确的是

　 (A)sinx = sin50°　　(B)sinx = -sin230°　　(C)sinx = -sin(-50°)　 (D)sinx = -sin490°

(87) 在三角形ABC中， = 6，角B等于60°, 则在方向上的投影为

　 (A) 3　　　　 (B)　　　　(C) – 3　　　　 (D)

(88) 已知=(x, 1) , = (2, 3x) , 则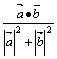的取值范围是

　　(A) ( -¥, )　　 (B) [0, ]　　 (C) [,]　　 (D)[,+¥]

(89) 下列四个命题：① 若^，则·=(·)²；　 ② (·)² = ²·²；

③ ½·½=½½·½½；　 ④ ½ + ½>½ - ½, 其中真命题的个数是

　 (A) 1个　　　 (B) 2个　　　 (C) 3个　　　 (D) 4个

(90) 已知函数f(x)=3-2x, g(x)=x²-2x,构造函数F(x), 定义如下:当f(x)≥g(x)时, F(x)=g(x); 当f(x)<g(x)时, F(x)=f(x). 那么F(x)

　 (A)有最大值3,最小值-1　　　　　　 (B)有最大值7-2,无最小值

(91) 已知，为不共线向量，则2-与+l(lÎR)共线的充要条件是

　 (A) l = 0　　 (B) l = -1　　　 (C) l = -2　　　 (D) l =

(92) 已知A(0, 3) , B(2, 0), C(- 1, 3) ，则与方向相反的单位向量是

　 (A) (0, 1)　　　 (B) (0, - 1)　　　(C) (-1, 1)　　　 (D) (1, -1)

(93) 等比数列{a _n}中，a₄×a ₆ =16, a₅ + a₇ = 6，则a₇的值是

　 (A) 2　　　　 (B)10　　　　 (C)2或10　　　　(D) 12

(94) 函数y = sinx(sinx+cosx)的单调递减区间是(其中kÎZ)

　 (A) [kp, kp]　　　　 (B) [kp, kp]

(95) 已知、是平面上的不共线向量，若= ，= ，点C分所成比为 -2，= l+ m，则l-m的值为

　 (A) 3　　　　 (B) – 3　　　　(C) 　　　　(D)

(96) 向量、、、满足关系式：= , , = = 1, , 则

+ 等于

(A) 7　　　　 (B) 　　　　(C) 　　　　(D)

(97) 在DABC中，a=3, b = 4, ÐC=30°, 则等于

(A) 　　　　(B) 　　　 (C) 　　　 (D) -12

(98)已知{a_n}是一个各项为正数的等比数列，且满足　　　　　　　　　，则公比的取值范围是

（A）(-1,1)È(1,+¥)　　　（B）(-¥, -1) È (1,+¥)　

（C）(0,1)È(1,+¥)　　　（D）(1,+¥)

(99)tanq 和tan(q)是方程x²+px+q=0的两个实根，则p, q满足

（A）p + q + 1 = 0　　　　　（B）p – q +1 = 0

（C）p + q – 1 = 0　　　　（D）p – q – 1 = 0

(100)已知DABC中, =(2,3), =(1, k)，且角B为直角，则实数k的值为

(A) 　　　　　 (B)　　　　 (C)　　　　 (D)

(101)DABC中, a = cos80°,　b=cos40°,　C=70°, 那么DABC的面积等于

(A) 　　　　　(B) 　　　　　(C)　　　　 (D)

(102)点(3, 4)按向量平移得到点(-2, 1), 则函数y = 2^x的图象按向量平移后的图象的解析式为

(A) y= 2^{x – 5}+3　　　(B) y= 2^{x –
5}-3　　　(C) y= 2^x
+5-3　　 (D) y= 2^{x +5}+3

(103)已知不共线，，，则M、N、P三点共线充要条件是

(A)k + l = 0　　　　(B) k - l = 0　　　 (C)k×l+1 = 0　　　 (D) k×l-1 = 0

(104)已知正六边形ABCDEF，在下列表达式 ①；②2；③；④2 中，与等价的有

(A) 1个　　　　 (B)2个　　　(C)3个　　　　 (D)4个

(105)DABC中, 若(sinA+sinB)(sinA – sinB) = sinC(sinA – sinC) ，则DABC中必有一内角等于

(A) 30°　　　 (B)45°　　　 (C)60°　　　　(D) 120°

(106)DABC中, 根据下列条件解三角形，其中有两解的是

(A) b=10,　A=45°,　C=70°　　　　　 (B) a = 60,　b = 48,　B= 60°

(107)在锐角三角形ABC中，a、b、c分别是角A、B、C的对边，ÐC=2ÐB，则的取值范围是

(A) (0, 2)　　　 (B) (, 2)　　　　(C) (,)　　　　(D) (, 2)

(108)把函数y = 的图象向左平移m(m>0)个单位，所得图象关于y轴对称，则实数m的最小值为

(A) 　　　　 (B) 　　　　 (C) 　　　 (D)

(109) 已知全集U = R，集合M={x lg x <0}，集合P={x £1}，则下列关系正确的是

　 (A)M　　C_U P　　　　(B)C_U P　　M　　 (C)M= C_U P　　　(D) ( C_U M) ÈP=R

(110)若a > b >c , a + b + c = 0, 则下面一定成立的不等式为

　 (A) ab > bc　　(B) ac < bc　　　(C) ab > bc　　 (D) a² > b² > c²

(111)不等式x(x-1)(x+2)(x-3)>0的解集是

　 (A)(3，+¥)　　　　 (B)(-¥，-2)　　　(C)(0，1)　　　　　　　　(D) (-¥,-2)È(0,1)È(3,+¥)

(112)若x=，则xÎ

　 (A)(3，4)　　　　 (B)(2，3)　　　　　　　(C)(1，2)　　　　　　　(D) (-2，-1)

(113)若正数x、y满足2x+y²=9，则x²y²的最大值是

　 (A) 3　　　 (B)9　　　 (C)27　　　 (D)81

(114)与同解的是

　 (A)(x-3)(2-x) ³ 0　　 (B)lg(x-2)£ 0　　　(C) 　　 (D)(x-3)(2-x)>0

(115)已知tan x = , (), 那么cos 的值为

　 (A)　　　 (B) –　　 (C) 　　(D) –

(116)已知函数y=f(x)对任意实数都有f(-x) = f(x), f(x)= - f(x+1)且在［０，１］上单调递减，则

(A)ｆ（）＜ｆ（）＜ｆ（）　(B)ｆ（）＜ｆ（）＜ｆ（）

(C)ｆ（）＜ｆ（）＜ｆ（）　(D).ｆ（）＜ｆ（）＜ｆ（）

(117)若x，cosx =，则x表示为

　 (A)arccos　 (B)arccos(-)　 (C)p+arccos(-)　　(D)p+arccos

(118)设0<a<1, 则下列大小关系正确的是

　 (A) 0.8^a <0.7 ^a　　　(B) a^0.8 > a^0.7　　　(C) 0.8 ^{l g
a} < 0.7 ^{l g a}　　(D)log_a0.8 > log_a 0.7

(119)定义在R上的奇函数¦(x)是减函数，设a+b £ 0，给出下列不等式：

①¦(a)¦(-a)£0　②¦(b)¦(-b)³0　③¦(a)+¦(b)£¦(-a)+¦(-b)　 ④¦(a)+¦(b)³¦(-a)+¦(-b)

其中成立的是　

　 (A)①与③　 (B)②与④　 (C)①与④　 (D)②与③

(120)已知a>1, 0<x<1, 0<y<1, 且log _ax × log _ay = 4, 则x×y

　 (A)有最大值a⁴　　 (B)有最小值a⁴　　　(C)有最大值a^{- 4}　　(D)有最小值a^{- 4}

(121) a、b、c、dÎR, 且ab > 0, , 则下列各式一定成立的是

(A) bc < ad　　　 (B) bc >ad　　　 (C)　　　 (D)

(122)如果且≠, 那么

(A) 　　　　　　　　　　　　　　　　 (B), lÎR

(123)设集合M ={x -1 £ x < 2} , N={xx ≤ a}. 若M∩N≠, 则a的取值范围是

(A) (- ¥, 2 )　　　 (B)(-1,+ ¥)　　 (C)[-1,+ ¥]　　　(D)[-1, 2]

(124)若x>0, y>0, 且4x+y= a，如果x×y的最大值是16，则常数a的值是

(A)8　　　　 (B)64　　　　 (C)32　　　 (D)16

(125)已知集合A= {x cosx < sinx, 0 £ x £ 2p }, B = {x tanx < sinx }, 那么A Ç B为

　 (A)(,p)　　　　(B)(,)　　　 (C)(p,)　　　 (D)(, )

(126)设a Î(0, 1)，则函数y = 的定义域为

　 (A)(1, 2)　　　　(B) (1, +¥)　　　　(C) [2, +¥]　　　 (D)( - ¥ , 2)

(127)一家旅社有100间相同的客房，经过一段时间经营实践，发现有如下表给出的关系，为使每天总收人达到最高，每间客房的每天定价应为：

每间每天定价	70元	60元	50元	40元
住房率	55％	65％	80％	95％

(A)70元　　　　　 (B) 60元　　　(C)50元　　　　　　(D) 40元

(128)二次函数f(x)的二次项系数为正，且对任意实数x，恒有f(2+x) = f(2－x), 若f(1－2x²)＜f(1+2x－x²)，则x的取值范围是

(A)　x＞2　　 　　　　　　　 (B) x＜-2或0＜x＜2

(129)若x > y >1, 且0 < a < 1，则下面结论中不正确的是

(A) x ^{– a} < y ^{– a}　　 (B) a^x < a^{– y}　　　(C) x^{– a}< y ^a　　　　(D) (log_a x)² < (log_a y)²

(130)已知tan>tan,那么下列命题成立的是

(A)若、是第三象限角，则cos<cosb　(B)若、是第二象限角，则sin>sinb

(C)若、是第四象限角，则sin>sinb　 (D)若、是第一象限角，则cos>cosb

(131)做一个面积为1平方米，形状为直角三角形的铁架框，有下列四种长度的铁管，最合理（够用，又浪费最少）的是

(A) 4.6米　　　　　　　　　　　　　　(B)4.8米　　　　　　　　　　　(C)5米　　　　　　　　　　　　(D)5.2米

(132)设ｗ>0，如果y＝2sinwx在［－，］上单调递增，那么ｗ的取值范围是

(A)　(0,]　　　　(B) (0,2]　　　　 (C)　(0,]　　　 (D) [2,+¥)

(133) 直线x+ay–a=0与直线ax– (2a–3)y–1= 0垂直，则a的值为

(A) a=2　　　　 (B) a= –3或a=1 　　 (C) a=2或a=0 　　 (D) a=1或a=0

(134)与椭圆共焦点，而与双曲线共渐近线的双曲线方程为

(A)　 (B)　 (C)　　(D)

(135)抛物线y= – ax²(a>0)的准线方程是

(A) x= 　　　　(B)x= – 　　　(C)y= – 　　　(D)y =

(136)给出下列曲线：①4x+2y – 1=0; ②x²+y²=3; ③+y²=1; ④– y ²=1，其中与直线y= -2x – 3 有交点的所有曲线是

(A) ①③　　　　(B)②④　　　　　　(C)①②③　　　　(D) ②③④

(137)圆C切轴于点M, 且过抛物线与轴的两个交点，O为原点，则OM的长是

(A)4 　　　 (B)　　　(C)　　　　(D)2

(138)已知圆(x – 3 )²＋(y＋4)²＝r²上至多有两点到直线4x – 3y – 4 =0的距离为1，则半径r的取值范围是

(A) (0，4]　　 (B) (0，5)　　 (C) (0，5] 　　 (D)[5，＋∞)

(139)直线l是双曲线=1(a>0，b>0)的右准线，以原点为圆心且过双曲线的焦点的圆，被直线l分成弧长为2∶1的两段圆弧，则该双曲线的离心率是

(A)　　　　　　　　 (B)　　　　　 (C) 　　　　　　 (D)

(140)方程与所表示的曲线在同一坐标系中的示意图应是　　　　　

(141)已知抛物线y = mx² + nx + k与抛物线y = x² – 5x +2关于点(3, 2)对称，则m + n + k 的值为

(A) 4　　　　 (B) 3　　　　 (C) 2　　　　　 (D)1

(142)已知A(1, 0)与直线l：x = 5, 若点p (3, a) (a ¹0)在以A为焦点，l为相应准线的圆锥曲线上，则此曲线必是

(A) 椭圆　　　　(B) 双曲线　　　 (C)抛物线　　　　(D) 圆

(143)若双曲线x²– y²=1右支上一点P（a，b）到直线y = x的距离是，则a+b的值为

（A）　　　　　　（B）　　　　（C）　　　　　　（D）2或-2

(144)若动点A（x₁, y₁），B（x₂, y₂）分别在直线l₁：x+y－7=0和l₂：x+y－5=0上移动，则AB中点M到原点距离的最小值为

(A)3　　　　 (B)2　　　　 (C)3　　　　(D)4

(145) 在空间，下列结论正确的是

　　(A) 任意两个向量一定是共面向量

　　(B) 若两条直线都和第三条直线垂直，则这两条直线平行

　 (D) 若两条直线没有公共点，则这两条直线平行

(146)棱锥被平行于底面的平面所截，截面把棱锥的高分成1：2(从顶点到截面与从截面到底面)，那么这个截面把棱锥的侧面分成两部分的面积之比等于　　　　　　　　　　　　　　　　　　　　　　　　　　　

　　(A)1：9　　　 (B)1：8　　　　 (C)1：4　　　　 (D)1：3

(147) 已知一个简单多面体的各个顶点都有三条棱，面数、顶点数分别为F，V，那么2F - V等于　　

　　　 (A) 2　　　　　　(B)4　　　　　　(C)8 　　　　(D)12

(148)已知长方体的表面积为11，其中12条棱长之和为24，则这个长方体的一条对角线长为

　 (A) 2　　　　(B)　　　 (C) 5　　　　　 (D)6

(149) 正方体ABCD-A₁B₁C₁D₁中，E为棱AB的中点，则直线C₁E与平面AA₁C₁C所成角的正切值为

(A)　　　　 (B)　　　　 (C)　　　　　 (D)

(150) 在空间四边形中，，则等于

(A) 　　 (B)

(151) 右图是正方体的平面展开图．在这个正方体中，

　　　 ①平行

　　　 ②CN与BE是异面直线

　　　 ③CN与BM成角

　　　 ④DM与BN垂直

　　　以上四个命题中，正确命题的序号是

　　　（A）①②③　　　　　　　（B）②④

　　　（C）③④　　　　　　　　　（D）②③④

(152) 已知三条直线m、n、l，三个平面a、b、g，下列四个命题中，正确的是

（A）　　　　　（B）

（C）　　　　　（D）

(153)在长方体ABCD-A₁B₁C₁D₁中，和与底面所成的角分别为和，则异面直线和所成角的余弦值为

(A) 　　　　　 (B) 　　　　　　 (C) 　　　　 (D)

(154) 已知空间四边形，其对角线为分别是的中点，点在线段上，且分所成的定比为2，现用基向量表示向量的值分别为

(A) 　　 (B)

(155) 设a、b为两条直线，、为两个平面，给出四个命题

①若,，且a∥,b∥,则∥;

②若∥,a⊥,b∥a,则b⊥;

③若a∥,a⊥,则⊥;

④若⊥,b⊥a,则b⊥.

上述命题中，正确的是

(A) ①②③④　　 (B) ①②③　　　 (C) ②③　　　 (D)③④

(156)在空间直角坐标系O-XYZ中，有一个平面多边形，它在XOY平面内的正射影的面积为8，在YOZ平面和ZOX平面内的正射影的面积都是6，则这个多边形的面积为

　　(A) 　　　　(B) 2　　　　(C) 　　　　 (D) 2

(157)点M(8, -10)按平移后的对应点N的坐标为(-7, 4)，则的坐标为

　 (A) (1, -6)　　 (B)(-15, 14)　　　 (C)(-15, -14)　　　 (D)(15, -14)

(158)在含有30个个体的总体中，抽取一个容量为5的样本，则个体a被抽到的概率为

　 (A) 　　　 (B)　　　 (C)　　　 (D)

(159)小王打算用70元购买面值为20元和30元的两种IC电话卡，若他至少买一张，则不同的买法一共有

(A)5种　　　(B)6种　　　 (C)7种　　　(D)8种

(160)从10种不同的作物种子中选出6种放入6个不同的瓶子中展出，如果甲、乙两种子不能放入1号瓶内，那么不同的放法共有

　 (A)　　 (B) 　　 (C) 　　 (D)

(161)已知(2^x – )⁹(xÎR)展开式的第7项为，则的值为

　 (A)　　　　 (B) 　　　　 (C)　　　　 (D)

(162)某城市新修建的一条道路上有12盏路灯，为了节省用电而又不能影响正常的照明，可以熄灭其中的3盏灯，但两端的灯不能熄灭，也不能熄灭相邻的两盏灯，则熄灭3盏灯的方法共有

　 (A)种　　　　(B) 种　　 (C) 种　　 (D) 种

(163)三边长均为整数，且最大边长为11的三角形的个数为

(A)25　　　　　(B)26　　　　　 (C)36　　　　　(D)　37

(164)给出下列四个命题：①“直线a, b是异面直线”的充分非必要条件是“直线a, b不相交”；②“直线l垂直于平面a内无数条直线”的充要条件是l^a；③“直线a^b”的充分非必要条件是“a垂直于b在平面a内的射影”；④“直线a//平面b”的必要非充分条件是“直线a至少平行于平面b内的一条直线”.其中正确的命题的个数是

　　(A)1个　　　(B)2个　　　 (C)3个　　　 (D)4个

(165)

(A) – 40　　　　(B) 10　　　　 (C) 40　　　　 (D) 45

(166)四面体的一个顶点A，从其它顶点和各棱的中点中取3个点，使它们和点A在同一平面内的取法有　　　　　　　　　　　　　　　　　　　

(A) 30种　　　 (B) 33种　　　 (C)36种　　　 (D) 39种

(167)将10个完全相同的小球全部装入编号为1, 2, 3的三个盒子中，要求每个盒子里小球的个数不少于盒子的编号数，这样的装法共有

　　(A)9种　　　　 (B) 12种　　　　 (C) 15种　　　　(D) 18种

(168) 袋中有红球、黄球、白球各1个，每次任取一个，有放回地抽取3次，则下列事件中概率是8/9的是

(A)颜色全相同　 (B)颜色不全相同　 (C)颜色全不同　　(D)颜色无红色

第二卷

(169) 把长、宽分别为4，3的矩形ABCD沿着对角线AC折成直二面角，则此时A、B、C、D四点所在球的内接正方体的表面积为　　　　　　　 .

(170) 在半径为R的球内有一个内接正三棱锥，它的底面的三个顶点恰在同一个大圆上，一个点从三棱锥一顶点出发沿着球面运动，经过其余三点后返回，则所经过的最短路程为

(171) 正三棱柱ABC-A₁B₁C₁的底面边长，侧棱长都是2，M为AB的中点，N为CC₁的中点，则在棱柱表面上，从M到N的最短路程长为　　　　　　　　 .

(172) 若不等式的斜率是_________.

(173) 抛物线的顶点是双曲线16x² – 9y² = 144的中心，而焦点是双曲线的左顶点，则此抛物线的方程为　　　　　　　　　 .

(174)若双曲线离心率为2，则它的两条渐近线的夹角等于___　　　　　　　 ____.

(175)已知双曲线-=1(a＞0,b＞0)的弦AB的中点为M，O为坐标原点，则直线OM和直线AB的斜率的乘积为　　　　　　　　　　　　　　　　　　　　　　　　.

(176) 两条平行直线分别经过点A（6，2）和B（-3 ，-1），各自绕着A、B旋转，若这两条平行线距离取最大时，两直线方程是　　　　　　　　　　　　　　　 .

(177)圆x²+y²+2x+4y—3=0上到直线x+y+1=0的距离为3的点有______个.

(178)椭圆按向量平移后得到的椭圆的准线方程为　　　　　　 .

(179)已知数列{a_n}满足a_n = n² + ln (nÎN*), 若不等式a_n < a_n+1对一切n³5且nÎN*都成立，则实数l的取值范围为　　　　　　　　　 .

(180) 从装有10个大小相同的小球（4个红球，3个绿球，3个黄球）的袋中任取2个，则取出两个同色球的概率是　　　　　　　　　　　　

(181)某兴趣小组中有6名男生和4名女生，从中任选4人组成代表队，则代表队中男生不超过2人的概率是　　　　 .

(182)从集合A=｛1,2,3,4,,10｝中，选出5个数组成集合A的子集M，使得这5个中的任何两个数的和不等于11，这样的子集M共有　　　　　　　个.

(183) 甲、乙两人解答三个问题，答对每题的概率分别为0.7和0.5，现在两人独立地解答这三个问题，则乙比甲得分高的概率为　　　　　　　 .

(184) 从男女团员共36名的支部中，选出2名代表，每人都有当选机会，如果选得的同性代表的概率为，则男女相差　　　　　名.

(185) 已知S_n = a₁+ a₂ a_n+1.

(1) 若数列{a_n}是首项为3，公比为2的等比数列，则的值=　　；

(2) 若数列{a_n}的通项公式为a_n = n – 1 , 且S_n <1000, 则n的最大值为　　 .

(186) 将函数y = 2x的图象按向量平移后得到函数y = 2x+6的图象，给出以下四个命题：①的坐标可以是(-3, 0); ②的坐标可以是(0, 6); ③的坐标可以是(-3, 0)和(0, 6); ④的坐标可以有无数种情况.

　其中是真命题为　　　　　　　　 (写出相应的命题序号即可).

(187) 一枚均匀的硬币掷10次，则从不接连出现正面的概率大小为　　　　　 .

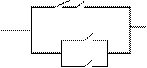(188) 如图，已知电路中4个开关闭合的概率都是1/2，且是相互独立的，求电路正常工作的概率。

(189)已知半圆的直径为AB=2r，半圆外的直线l与BA的延长线垂直且交于G点，½AG½=2a，（2a<）半圆上有相异两点M和N。它们与直线l的距离分别为d₁、d₂，d₁ ==½MA½，d₂=½NA½，求证：½AM½+½AN½=2r.

(190)有甲、乙两只口袋，甲袋装有4个白球2个黑球，乙袋装有3个白球和4个黑球，若从甲、乙两袋中各任取出两球后并交换放入袋中．

　　（1）求甲袋内恰好有2个白球的概率；

（2）求甲袋内恰好有4个白球的概率；

(191)甲、乙队进行篮球总决赛，比赛规则为：七场四胜制，即甲或乙队，谁先累计获胜四场比赛时，该队就是总决赛的冠军，若在每场比赛中，甲队获胜的概率均为0.6，每场比赛必须分出胜负，且每场比赛的胜或负不影响下一场比赛的胜或负．

　　（1）求甲队在第五场比赛后获得冠军的概率；

　　（2）求甲队获得冠军的概率；

(192) 在直三棱柱ABC-A₁B₁C₁中，底面是等腰直角三角形，ÐACB=90°，侧棱AA₁=2，D、E分别是CC₁与A₁B的中点，点E在平面ABD上的射影是DABD的重心。

(1)　　求A₁B与平面ABD所成角的大小；

(2)　　求点A₁到平面AED的距离.

(193) 如图，四棱锥S—ABCD中，底面ABCD为矩形，侧面SCD为直角三角形,∠SCD=

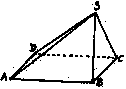90°，二面角S—CD—B=60°，BC=a,AB=SC=2a.

(Ⅰ)求证：平面SAB⊥平面ABCD；

(Ⅱ)求点C到平面SAD的距离.

(194) 三角形ABC中，a, b, c为内角A、B、C的对边，若a, b, 3c成等比数列，且A – C = , 试求A、B、C的值.

(195) 已知数列{b_n}是等差数列，b₁ = 1, b₁ + b₂+ …+b₁₀ = 145.

(1)求数列{b _n}通项公式；

　 (2)设数列{a_n}的通项a_n = log_a (1+) (其中a>0且a ¹ 1)，记S _n是数列{a_n}的前n项和，试比较S_n与的大小，并证明你的结论.

(196) 已知二次函数f(x) = ax² +bx+c和函数g(x) = - bx，其中a>b>c,且a+b+c = 0 .

(1)求的取值范围；

(2)求证：函数f(x)与g(x)的图象必有两个不同的交点A、B；

(3)求线段AB在x轴上的射影A₁B₁的取值范围.

(197) 函数f(x)=log_a(x－3a)(a＞0,且a≠1),当点P（x,y)是函数y=f(x)图象上的点时，Q（x－2a,－y)是函数y=g(x)图象上的点.

（Ⅰ）写出函数y=g(x)的解析式.

（Ⅱ）当x∈［a+2,a+3］时，恒有f(x)－g(x)≤1,试确定a的取值范围.

(198)设点P(x,y)经过变换(*)变为点Q()，

①点P₁(x₁,y₁), P₂(x₂,y₂)经过变换 (*)变为点Q₁()，Q₂()，试探索线段长度P₁P₂与Q₁Q₂之间的数量关系

②是否存在这样的直线：它上面的任一点经变换（*）后得到的点仍在该直线上？若存在，试求出所有这些直线；若不存在，则说明理由。

③可以证明，作为点的集合，直线、射线、线段和角经变换（*）依次仍变为直线、射线、线段和角，设点P₁，P₂，P₃,不在一直线上，∠P₁P₂P₃经变换（*）变为∠Q₁Q₂Q₃，问是否总有“∠P₁P₂P₃=∠Q₁Q₂Q₃，”？请简述主要理由