高二数学复数模拟训练
一. 选择题:
1. 复数![]() 化成三角形式,正确的是( )
化成三角形式,正确的是( )
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
2. 复数![]() 的辐角主值是( )
的辐角主值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
3. 两个复数![]() 的模与辐角分别相等,是
的模与辐角分别相等,是![]() 成立的( )条件。
成立的( )条件。
A. 充分不必要 B. 必要不充分 C. 充要 D. 既不充分又不必要
4. 若复数z满足![]() ,则
,则![]() 的最小值为( )
的最小值为( )
A. 1 B. 2 C. ![]() D.
D. ![]()
5. 把复数![]()
![]() 在复平面内对应的向量值O点按顺时针方向旋转
在复平面内对应的向量值O点按顺时针方向旋转![]() 后所得向量对应的复数为( )
后所得向量对应的复数为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
6. 复数![]() 的三角形式是( )
的三角形式是( )
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
7. 设![]() 的辐角主值为
的辐角主值为![]() ,则
,则![]() 的辐角主值是( )
的辐角主值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
8. 设![]() ,
,![]() ,
,![]() ,则
,则![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
二. 填空题:
1. 若复数z满足![]() ,则
,则![]() =_______。
=_______。
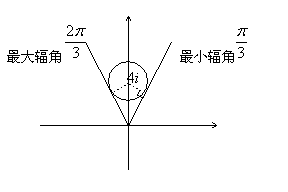
2. 若动点P对应的复数为z,且满足![]() ,则z的辐角主值的范围为______,z取得最大值时,z=_______。
,则z的辐角主值的范围为______,z取得最大值时,z=_______。
3. ![]() 的三角形式为_______。
的三角形式为_______。
4. 将复数![]() 所表示的向量绕原点按逆时针方向旋转
所表示的向量绕原点按逆时针方向旋转![]() 角
角![]() 所得的向量对应的复数为-2,则
所得的向量对应的复数为-2,则![]() ______。
______。
5. 复平面内向量![]() 对应的复数为
对应的复数为![]() ,A点对应的复数为-1,现将
,A点对应的复数为-1,现将![]() 绕A点顺时针方向旋转
绕A点顺时针方向旋转![]() 后得到的向量为
后得到的向量为![]() ,则点C对应的复数为_______。
,则点C对应的复数为_______。
三. 解答题:
1. 已知![]() ,求复数
,求复数![]() 。
。
2. 已知:A(2,0)为定点,在单位圆上有一动点P,以AP为一边按逆时针方向作等边![]() 。
。
求:点Q的轨迹方程。
四. 思考题:
设![]() ,若
,若![]() ,求证:
,求证:![]() ,试用多种方法证明。
,试用多种方法证明。
【试题答案】
一.
1. A 2. C 3. A 4. B
5. C 6. A 7. A 8. C
二.
1. ![]()
提示:运用整体思想,设![]() ,则
,则![]()
![]() ,从而可由
,从而可由![]() 解出未知数z。
解出未知数z。
2. ![]() ,当
,当![]() 取最大值时,
取最大值时,![]()
提示:结合图形,即把代数问题几何化、图形化,见下图:
3. ![]()
4. ![]()
5. 点C对应复数为![]()
提示:![]() ,而
,而![]()
三.
1. 解:设![]() ,则
,则![]()
![]() (1)
(1)
![]() 即
即 ![]() (2)
(2)
联立(1)(2),解得![]() 或
或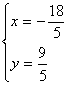 (经检验,
(经检验,![]() 为增根,应舍去)
为增根,应舍去)
![]()
2. 解:设![]() 点P在单位圆上
点P在单位圆上
![]() 点P的坐标为
点P的坐标为![]()
它表示的复数为![]()
![]() 表示复数为
表示复数为![]()
![]() 是
是![]() 绕A逆时针旋转
绕A逆时针旋转![]() 得到的
得到的
![]() 表示的复数为
表示的复数为![]()
![]()
从而![]() 表示的复数为
表示的复数为
![]()
![]()
设点Q坐标为(x,y),则有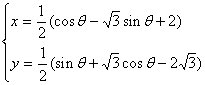 (
(![]() 为参数)
为参数)
消去参数![]() ,得
,得![]()
![]() 点Q的轨迹方程为
点Q的轨迹方程为![]()
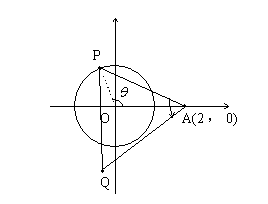
四. 略