不等式的证明章节试题

一. 习题：

  1. 求证：

  2. 为正数，求证：

  3. 已知：，求证：

  4. 已知：，求证：

  5. 已知：，求证：

  6. 设，证明不等式：

  7. 已知：，求证：

二. 练习：

  1. 若，求证：

  2. ，记，则的大小关系为（　　）

　　A. 　　　　　B. 　　　　　 C. 　　　　　 D.

  3. ，则与的大小关系是

（　　）

　　A. 　　　　　 B. 　　　　　　C. 　　　　　　D.

  4. 实数满足什么条件时，？

  5. 若，比较与的大小。

【试题答案】

一. 例题：

  1. 求证：

　　证明：

　　　　

　　另：

　　

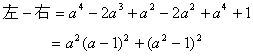
  2. 证明：

　　　　　　　　 

　　证毕

　　法二：分析法：

　　要证不等式成立，即证

　　而

　　即（*）成立

　　证毕

  3. 法一：

　　　　 

　　

　　（当且仅当，“”成立）

　　又

　　（当且仅当，“”成立）

　　

　　

　　

　　得：

　　法二：要证

　　只需证

　　

　　只需证

　　即

　　只需证或

　　

　　

　　又不可能

　　只有，（*）成立

　　原不等式成立

  4. 证法一：

　　同理：

　　

　　三式相加即可

　　法二：

　　又

　　

　　(1)、(2)及传递性得

　　同理：

　　

  5. 证明：

　　　　　　 

　　　　　　 

　　此不等式是轮换对称式

　　不妨设

　　

　　

　　同理：

　　

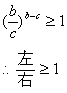
　　证毕

  6. 证法一：要证原不等式

　　只需证：

　　只需证：

　　只需证：

　　显然

　　

　　证法二：

　　　　　　　　　　　 

　　

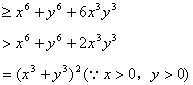
  7. 证法一：要证

　　只要证

　　即证

　　就是

　　成立（略）

　　

　　证法二：

　　　　　　　　　　　　

　　

　　

　　

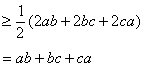
　　证法三：

　　　　　　　　　　　 

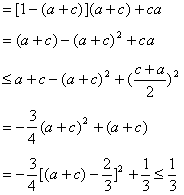
二. 练习：

  1. 证：

　　

　　两边取以10为底的对数得：

  2. D

　　

　　

  3. C

　　

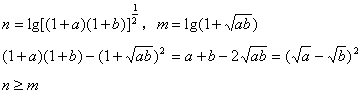
  4. 解：

　　由定理5：

　　即

  　

　　亦即

　　

　　

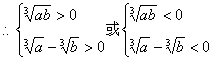
　　即

  5. 解：

　　　　

　　　　

　　　　

　　

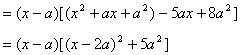
　　与不同时为0

　　

　　时，

　　时，