第四讲　函数的单调性与奇偶性

一、内容摘要

1．　　 函数是奇(或偶)函数的定义；一函数是奇(或偶)函数的必要条件；函数奇偶性的判定方法；奇(或偶)函数的性质；两函数的和、差、积、商、复合的奇偶性的判定．

2．　　函数单调性的定义；常见函数的单调区间；函数单调性的证明；两函数的和、差、积、商、复合的单调性的判定．

3．　　函数的奇偶性与单调性的综合应用．

二、基本训练

1．　　 函数在区间[－2，+∞]上是增函数，则的取值范围是
（A）≥25　　　　 （B）=25　　（C）≤25　　　（D）＜25

2．　　 函数的单调性的正确说法是
（A）单调递减函数
（B）在(－∞，0)上是减函数，在(0，+∞)上是增函数
（C）在(－∞，1)上是减函数，在(1，+∞)上是减函数
（D）除=1点外，在(－∞，+∞)上是单调递减函数

3．　　 已知函数，则是：
（A）奇函数　　　　　　　　　　　  （B）偶函数
（C）既是奇函数又是偶函数　　　　  （D）非奇非偶函数

4．　　 函数
（A）奇函数　　　　　　　　　　　  （B）偶函数
（C）既是奇函数又是偶函数　　　　  （D）非奇非偶函数

5．　　 已知函数是偶函数，则在(－∞，3)内是
（A）增函数　　　　　　　　　　　  （B）有一部分递增另一部分递减
（C）减函数　　　　　　　　　　　  （D）不能确定增减性

6．　　 已知函数在上是增函数，函数是偶函数，则
　(A)　　　 (B)  
　(C) 　　　(D)

7．　　 已知为偶函数，为奇函数，且，则有=＿＿＿＿＿；=＿＿＿＿＿．

8．　　 （1）函数的递增区间是＿＿＿＿＿．；
（2）函数的递减区间是＿＿＿＿＿．

9．　　 若为偶函数，其定义域为R，且在[0，+∞]上是减函数，则与的大小关系是＿＿＿＿＿．

10． 已知是定义在Ｒ上的偶函数，且它在上单调递增，那么使的实数的取值范围是＿＿＿＿．

11． 函数的反函数是＿＿＿＿．

12． 证明函数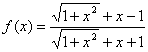的图象关于原点对称。

13． 已知常数满足，求证函数在上为减函数。

14． 讨论函数的单调性．

15． 讨论函数在的增减性

16． 已知函数在区间(－∞，+∞)上是增函数，∈R．
(1)证明：如果≥0，那么；
(2)判断(1)中命题的逆命题是否正确，请证明你的结论．

17． 已知函数是定义在R^*上的减函数，并且满足，，（1）求的值；（2）如果，求的取值范围．

18． 已知奇函数在定义域为(－1，1) 上单调递减，且满足条件： 的的取值范围．

19． 定义在R上的函数对一切有，且，试判断的奇偶性．

20． 求函数的反函数．

21． 若点（1，2）既在函数的图象上，又在它的反函数的图象上，求的值．

22．

23． 已知函数的定义域是R，且对任意实数总有成立，求证是偶函数． 

24． 若是定义在R上的偶函数，且当≥0时为增函数，那么使＜的实数的取值范围是＿＿＿＿＿．

25． 已知函数是奇函数，当，时，那么当时，的表达式是＿＿＿＿．

26． 用定义证明在上是增函数

27． 函数是偶函数，且不恒等于0，则为
（A）奇函数　　（B）偶函数　 （C）可能是奇函数，也可能是偶函数
（D）既不是奇函数，也不是偶函数

28． 求下列函数的单调区间：

29． 下列函数中，在(－∞，0)内是减函数的有
（A）　　（B）　　（C）　　（D）

30． 已知函数是奇函数，函数g在区间(－∞，3)为上减函数，在(3，+∞)上为增函数，求实数的值．

31． 已知函数满足以下条件：定义域是一个闭区间，在定义域上严格单调，，，最大为，求的定义域和值域．

32． 判断下列函数的奇偶性
（1）　　（2）

33． 判断函数在区间上的单调性，并用定义加以证明．

34． 已知是上的单调递增函数，求实数的取值范围．

35． 已知奇函数满足下列两个条件：
①存在常数p＞0使f (p)＝1；②当f (x₁)，f (x₂)，f (x₁－x₂)都有意义且f (x₁)≠f (x₂)时，．
⑴求f (2p)、f (3p)、f (5p)的值；
⑵求证一定存在常数T，使得f (x＋T)＝f (x)；
⑶若0＜x＜2p时，f (x)＞0，求证：f (x)在区间(0，4p)上是单调递减函数．

36． 如果函数在区间上是减函数，求实数的取值范围．

37． 已知是定义在Ｒ上的奇函数，当时，，求在Ｒ上的表达式．

38． 设是定义在Ｒ上的偶函数，且它的图象关于直线对称，已知时，，求当时的表达式．

39． 若函数不恒等于0与的图象关于原点对称，则
（A）是奇函数不是偶函数　　　　（B）是偶函数不是奇函数
（C）既奇函数又是偶函数　　　　（D）非奇非偶函数

40． 在所有定义域为R的函数中，一定不存在的函数是
（A）既是增函数，又是奇函数　　　（B）既是奇函数，又是偶函数
（C）既是偶函数，又有反函数　　　（D）两个互为反函数的函数是同一函数

41． 奇函数在[3，7]上为增函数，且最小值5，则在[－7，－3]上是 
（A）增函数且最小值为－5　　　　　  （B）增函数且最大值为－5
（C）减函数且最小值为－5　　　　　  （D）减函数且最大值为－5

42． 设为定义在(－∞，+∞)上的偶函数，且在[0，+∞]上为增函数，则，，的大小顺序是
（A）　　　　  （B）
（C）　　　　　 （D）

43． 已知函数是R上偶函数，当x＜0时，为增函数，对于＜0，＜0，有，则
（A）（B）（C）
（D）与关系不确定

44． 已知函数的最小正周期为8，且等式对一切实数x成立，则为
（A）奇函数非偶函数　　　　　　　　　 （B）偶函数非奇函数
（C）奇函数也是偶函数　　　　　　　 （D）非奇非偶函数

45． 若是偶函数，则＿＿＿＿＿．

46． 已知是定义在Ｒ上的奇函数，且，若当时，，则＿＿＿．

47． 已知函数是R上的偶函数，当≥0时，。
（1）用分段函数写出函数表达式；
（2）利用对称性画出其图象；
（3）指出其单调区间；
（4）利用图象指出在什么区间上＞0，在什么区间上＜0；
（5）求出函数的最值．

48． 求证函数在区间上单调递减