第三讲 映射与函数、
函数的定义域及值域
一、内容摘要
1. 函数的表示方法通常有三种:解析法、列表法、图象法.
2. 求函数的定义域即是求不等式组的解集.
3. 求函数值域的方法常有:①直接法;②配方法;③“△” 法;④换元法;⑤利用函数的性质等.
二、练习与例题
1.
设X={x0≤x≤2},Y={y0≤y≤1},则从X到Y可建立映射的对应法则是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
2. 设![]() 在映射
在映射![]() 下的象是
下的象是![]() ,则
,则![]() 在
在![]() 下的原象是
下的原象是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
3. 下列哪一个对应是从集合A到集合B的映射
(A)A={平面M内的四边形},B={平面M内的圆},对应法则是作“四边形的外接圆”.
(B)A={平面M内的圆},B={平面M内的矩形},对应法则是“作圆的内接矩形”.
(C)A={平面M内的点对},B={平面M内的矩形},对应法则是以点对为相对顶点作矩形.
(D)A={平面M内的三角形},B={平面M内的圆},对应法则是“作三角形的内切圆”.
4.
下列各组函数中表示同一函数的是
(A)![]() 与
与![]() (B)
(B)![]() 与
与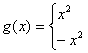
![]()
(C)![]() 与
与![]() (D)
(D)![]() 与
与![]()
5. 设![]() ,则
,则![]() 的表达式为
的表达式为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
6.
已知![]() ,则
,则![]() 等于
等于
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
7.
下列函数的值域:
①![]() ②
②![]() ③
③![]()
④ ![]() ⑤
⑤![]() ⑥
⑥![]()
⑦*![]()
8.
求下列函数的定义域:
(1)![]() (2)
(2)![]()
9. 当![]() 为_____时,函数
为_____时,函数![]() 的定义域为R.
的定义域为R.
10. 设![]() ,
,![]() ,若
,若![]() 则
则![]() _____.
_____.
11. 函数![]() 满足条件
满足条件![]() ,求
,求![]() 的解析式_____.
的解析式_____.
12.
若![]() ,则
,则![]() 的值域是_____.
的值域是_____.
13.
函数![]() 的定义域为R*,若对于定义域内任意的
的定义域为R*,若对于定义域内任意的![]() 均有
均有![]() ,又已知
,又已知![]()
![]() ,用
,用![]() 表示
表示![]() 的值,
的值,![]() =_____.
=_____.
14.
在测量某物理量的过程中,因仪器和观察的误差,使得![]() 次测量分别得到
次测量分别得到![]() ,共
,共![]() 个数据.我们规定此测量物理量的“最佳近似值”
个数据.我们规定此测量物理量的“最佳近似值”![]() 是这样一个量:与其他近似值比较
是这样一个量:与其他近似值比较![]() 与各数据的差的平方和最小,依此规定,从
与各数据的差的平方和最小,依此规定,从![]() 可推出的
可推出的![]() =_____.
=_____.
15.
(1)设![]() 的值域是[-1,4],求a,b的值;
的值域是[-1,4],求a,b的值;
(2)已知函数![]() 的值域是
的值域是![]() ,求
,求![]() 的值.
的值.
16.
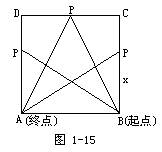 在边长为4的正方形ABCD的边上有一点P沿着折线BCDA,由B点(起点)向A(终点)移动,设P点移动的路程为
在边长为4的正方形ABCD的边上有一点P沿着折线BCDA,由B点(起点)向A(终点)移动,设P点移动的路程为![]() ,△ABP的面积为
,△ABP的面积为![]() .
.
(1)求△ABP的面积与点P移动的路程间的函数关系式.
(2)作出函数的图象.
17.
已知函数![]() 的值域为
的值域为![]() ,求
,求![]() 的值
的值