平面填空题28题
1、平面是几何中最基本的概念之一,在数学中对这一类概念,不加以_____,而只进行_____。翰林汇
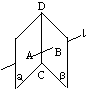
2、填写适当符号:如图,A___a,A____b,A____![]() ,a____b= _____,AB_____b= _____。
,a____b= _____,AB_____b= _____。
翰林汇
3、共点的三条直线三条或两条直线可以确定平面的个数为___________.翰林汇
4、三棱锥P-ABC,PA=PB=PC=![]() ,AB=10,BC=8,CA=6,则二面角P-AC-B的大小为____翰林汇
,AB=10,BC=8,CA=6,则二面角P-AC-B的大小为____翰林汇
5、![]()
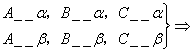
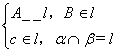 翰林汇
翰林汇
6、空间不共线的四个点可确定 个平面.翰林汇
7、平面M、N不重合,在M内取4个点,在N内取5个点,这些点最多能确定的平面有_______个翰林汇
8、四条直线过同一点,过每两条直线作一个平面,则可以作________________个不同的平面。
9、互相平行的四条直线,每两条确定一个平面最多可确定____个平面,最少可确定______个平面。翰林汇
10、平面M、N不重合, 在M内取4个点, 在N内取5个点, 这些点最多确定________个平面.翰林汇
11、过一点作n个不同的平面(n≥2),这些平面最多有k条交线,最少有l条交线,则k、l分别为________.翰林汇
12、a、b是异面直线,a上有m个点,b上有n个点(m≥2,n≥2),这m+n个点一共可以确定________个平面.翰林汇
13、平面![]() 、
、![]() 、
、![]() 两两互相垂直,O是它们的公共点,点P到
两两互相垂直,O是它们的公共点,点P到![]() 、
、![]() 、
、![]() 的距离分别为2cm、3cm、6cm,则P到O的距离为________.翰林汇
的距离分别为2cm、3cm、6cm,则P到O的距离为________.翰林汇
14、长方体的六个面所在的平面将空间分成________.翰林汇
15、P为边长为a的正三角形ABC所在平面外一点且PA=PB=PC=a,则P到AB的距离为______。翰林汇
16、一条直线和直线外三点,可能确定的平面个数是____。翰林汇
17、不重合的三条直线交于一点,最多能确定 个平面;相交于两点,最多能确定 个平面;相交于三点,最多能确定 个平面。
18、与空间四个点的距离都相等的平面有____个。翰林汇
19、三个平面把空间分成m个部分, m 的值的_____。翰林汇
20、在正方体中,所有面上的对角线与正方体的一条对角线垂直的条数是__条。翰林汇
21、如果直线l1和l2不重合,那么它们能确定的平面个数是____。翰林汇
22、如果直线![]() 过平面a内一点,与a外一点A,那么
过平面a内一点,与a外一点A,那么![]() 和平面a______公共点,这是因为,若假设至少有两个公共点,那么
和平面a______公共点,这是因为,若假设至少有两个公共点,那么![]() _____a,又A_____
_____a,又A_____![]() ,故A______a,这与_____相矛盾。翰林汇
,故A______a,这与_____相矛盾。翰林汇
23、两两相交的三条直线,仅当交点个数等于___时,这三条直线才可能不共面。翰林汇
24、A、B、C、D是不共面的四点,它们到平面M的距离之比,依次为1: 1:1:2,那满足条件的平面M的个数为____。翰林汇
25、两两个相交且不交于同一点的四条直线可能确定的平面个数是______。翰林汇
26、设直线![]() 与平面a所成的角为q,则q的范围是____。翰林汇
与平面a所成的角为q,则q的范围是____。翰林汇
27、过平面外一点,作已知平面的垂直平面有___个。翰林汇
28、三条直线两两相交,至少过其中三个点的平面有____个。
平面填空题28题(参考答案)
1、 定义,描述翰林汇 2、 Î,Ï,Î,∩,CD,∩,B。翰林汇
3、 1或3翰林汇 4、 ![]() 翰林汇
翰林汇
5、 ![]() 翰林汇
翰林汇
6、 1个或4个翰林汇 7、 72翰林汇
8、 1个,4个或6个翰林汇 9、 6个,1个翰林汇
10、 72翰林汇
11、 C![]() ,1翰林汇
,1翰林汇
12、 m+n翰林汇 13、 7cm翰林汇
14、 27 翰林汇15、 ![]() a翰林汇
a翰林汇
16、 1或2或3或4个翰林汇 17、 3个,2个,1个翰林汇
18、 7个或无数个翰林汇 19、 4或6或7或8翰林汇
20、 6翰林汇 21、 0个或1个翰林汇
22、 只有一个,Ì,Î,Î,AÏa翰林汇
23、 1 翰林汇24、 7翰林汇
25、 1翰林汇 26、 00£q£900翰林汇
27、 无数个翰林汇 28、 1个或3个