高二下学期数学单元六

椭圆

一、选择题：本大题共12小题，每小题5分，共60分．请将唯一正确结论的代号填入题后的括号内．

1．椭圆＝１的准线平行于x轴，则实数m的取值范围是　　　　　　 （ 　）

　 A．－１＜m＜３　　　　　　　　  　　B．－＜m＜3且m≠0　　

　 C．－１＜m＜３且m≠0　　　　　　  　D．m＜－1且m≠0

2． a、b、c、p分别表示椭圆的半长轴、半短轴、半焦距、焦点到相应准线的距离，则它们

的关系是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　 A．p=　　　　　 B．p=　　　　　C．p=　　　　　 D．p=

3．短轴长为，离心率为的椭圆的两个焦点分别为F₁、F₂，过F₁作直线交椭圆于A、B

两点，则ΔABF₂的周长为　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　 A．24　　　　　　　B．12　　　　　　C．6　　　　　　　 D．3

4．下列命题是真命题的是　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　 A．到两定点距离之和为常数的点的轨迹是椭圆

　 B．到定直线x=和定F(c，0)的距离之比为的点的轨迹是椭圆

　 C．到定点F(-c，0)和定直线x=-的距离之比为(a>c>0)的点的轨迹 是左半个椭圆

　 D．到定直线x=和定点F(c，0)的距离之比为(a>c>0)的点的轨迹是椭圆

5．P是椭圆+=1上任意一点，F₁、F₂是焦点，那么∠F₁PF₂的最大值是　　　　（　　）

　 A．60⁰　　　　　  B．30⁰　　　　　 C．120⁰　　　　　 D．90⁰

6．椭圆+=1上一点P到右准线的距离是2b，则该点到椭圆左焦点的距离是（　　）

　 A．b　　　　　　　 B．b　　 　　　C．b　　　　　 D．2b

7．椭圆+=1的焦点为F₁和F₂，点P在椭圆上，如果线段F₁P的中点在y轴上，那么

PF₁是PF₂的　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　  ）

　 A．7倍　　　　　　B．5倍　　 　　　C．4倍　　 　　　 D．3倍

8．设椭圆+=1(a>b>0)的两个焦点是F₁和F₂，长轴是A₁A₂，P是椭圆上异于A₁、A₂的

点，考虑如下四个命题：

①PF₁-A₁F₁=A₁F₂-PF₂；　　　　②a-c<PF₁<a+c；

③若b越接近于a，则离心率越接近于1；

④直线PA₁与PA₂的斜率之积等于-．

其中正确的命题是　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　 A．①②④　　　　　B．①②③　　　　C．②③④　　　　　D．①④

9．过点Ｍ（－２，０）的直线l与椭圆x²＋2y²＝2交于Ｐ_１、Ｐ_２两点，线段Ｐ_１Ｐ_２的中点

为Ｐ，设直线l的斜率为k₁（k₁≠0），直线ＯＰ的斜率为k₂，则k₁k₂的值为　 （　　）

　 A．２　　　　  　　B．－２　　　 　 C．　　　　　 　 D．－

10．已知椭圆+=1(a>b>0)的两顶点A(a，0)、B(0，b)，右焦点为F，且F到直线AB的距离等于F到原点的距离，则椭圆的离心率e满足　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　 A．0<e<　　　　 B．<e<1　　　 C． 0<e<-1　　 D．-1<e<1

11．设Ｆ_１、Ｆ_２是椭圆＝１（a＞b＞0）的两个焦点，以Ｆ_１为圆心，且过椭圆中心的圆与椭圆的一个交点为Ｍ，若直线Ｆ_２Ｍ与圆Ｆ_１相切，则该椭圆的离心率是（　　）

　 A．２－　　 　 B．－１　 　　C．　　　　 　　D．

12．在椭圆+=1内有一点P（1，-1），F为椭圆右焦点，在椭圆上有一点M，使MP+2MF的值最小，则这一最小值是`　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　 A．　　　　 　　 B．　　　　　　C．3　　　　　　　 D．4

二、填空题：本大题共4小题，每小题4分，共16分．请将最简结果填入题中的横线上．

13．椭圆+=1的离心率是2x²-11x+5=0的根，则k= 　　　　 ．

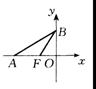14．如图，∠ＯＦＢ＝，Ｓ_ΔＡＢＦ＝２－，则以ＯＡ为长半轴，ＯＢ

 为短半轴，Ｆ为一个焦点的椭圆的标准方程为　　　　．

15．过椭圆＝１的下焦点，且与圆x²＋y²－3x＋y＋＝0相切

的直线的斜率是　　　　　．

16．过椭圆+=1的左焦点作一条长为的弦AB，将椭圆绕其左准线旋转一周，则

弦AB扫过的面积为　　　　 ．

三、解答题：本大题共6小题，共74分．解答题应写出必要的计算步骤或推理过程．

17．（本小题满分12分）

已知A、B为椭圆+=1上两点，F₂为椭圆的右焦点，若AF₂+BF₂=a，AB中点到椭圆左准线的距离为，求该椭圆方程．

18．（本小题满分12分）

设中心在原点，焦点在x轴上的椭圆的离心率为，并且椭圆与圆x²+y²-4x-2y+=0交于A、B两点，若线段AB的长等于圆的直径．

（1）　　　 求直线AB的方程；

（2）　　　 求椭圆的方程．

19．（本小题满分12分）

已知+=1的焦点F₁、F₂，在直线l：x+y-6=0上找一点M，求以F₁、F₂为焦点，通过点M且长轴最短的椭圆方程．

20．（本小题满分12分）

一条变动的直线l与椭圆+=1交于P、Q两点，M是l上的动点，满足关系MP·MQ=2．若直线l在变动过程中始终保持其斜率等于1．求动点M的轨迹方程，并说明曲线的形状．

21．（本小题满分12分）

设椭圆+=1的两焦点为F₁、F₂，长轴两端点为A₁、A₂．

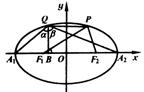
（1）　　　 P是椭圆上一点，且∠F₁PF₂=60⁰，求ΔF₁PF₂的面积；

（2）　　　 若椭圆上存在一点Q，使∠A₁QA₂=120⁰，求椭圆离心率e的取值范围．

22．（本小题满分14分）

已知椭圆的一个顶点为Ａ（０，－１），焦点在x轴上，若右焦点到直线x－y＋2＝0的距离为３．

（1）求椭圆的方程；

（2）设椭圆与直线y＝kx＋m（k≠0）相交于不同的两点Ｍ、Ｎ，当｜ＡＭ｜＝｜ＡＮ｜时，求m的取值范围．

单元六

一、B D C D A　 A A AＤC  B C

二、13．4或　　　14．　　　　 15．　　　 16．18π

三、17．解：设A(x₁，y₁)，B(x₂，y₂)，由焦点半径公式有a-ex₁+a-ex₂=a，∴x₁+x₂=a(∵e=)，即AB中点横坐标为a，又左准线方程为x=-a，∴a+a=，即a=1，∴椭圆方程为x²+y²=1．

18．解：（1）直线AB的方程为y=-x+2；　 （2）所求椭圆的方程为+=1．

19．解：由+=1，得F₁（2，0），F₂（-2，0），F₁关于直线l的对称点F₁^/（6，4），连F₁^/F₂交l于一点，即为所求的点M，∴2a=MF₁+MF₂=F₁^/F₂=4，∴a=2，又c=2，∴b²=16，故所求椭圆方程为+=1．

20．解：设动点M(x，y)，动直线l：y=x+m，并设P(x₁，y₁)，Q(x₂，y₂)是方程组的解，消去y，得3x²+4mx+2m²-4=0，其Δ=16m²-12(2m²-4)>0，∴-<m<，x₁+x₂=-，

x₁x₂=，故MP=x-x₁，MQ=x-x₂．由MPMQ=2，得x-x₁x-x₂=1，也即x²-(x₁+x₂)x+x₁x₂=1，于是有x²++=1．∵m=y-x，∴x²+2y²-4=3．由x²+2y²-4=3，得椭圆+=1夹在直线y=x±间两段弧，且不包含端点．由x²+2y²-4=-3，得椭圆x²+2y²=1．

21．解：（1）设PF₁=r₁，PF₂=r₂，则S=r₁r₂sin∠F₁PF₂，由r₁+r₂=2a，　　

4c²=r₁²+r₂²-2cos∠F₁PF₂，得r₁r₂=．代入面积公式，得

S=b²=b²tg∠=b²．

（2）设∠A₁QB=α，∠A₂QB=β，点Q(x₀，y₀)(0<y₀<b)．tgθ=tg(α+β)==

=．∵+=1，∴x₀²=a²--y₀²．∴tgθ= ==-．

∴2ab²≤c²y₀≤c²b， 即3c⁴+4a²c²-4a⁴≥0，∴3e⁴+4e²-4≥0，解之得e²≥，∴≤e<1为所求．

22．解：（1）用待定系数法．椭圆方程为＝１．

（2）设Ｐ为弦ＭＮ的中点．由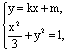得（3k²＋1）x²＋6kmx＋3（m²－1）＝0．由Δ＞０，得m²＜3k²＋1　①，∴x_P＝，从而，y_P＝kx_p＋m＝．∴k_AP＝．由ＭＮ⊥ＡＰ，得＝－，即2m＝3k²＋1　②．将②代入①，得2m＞m²，解得０＜m＜2．由②得k²＝＞０．解得m＞．故所求m的取值范围为（，２）．