高二年级第一学期期末综合测试题

一、选择题（本大题共25小题，每小题2分，共50分）

1、　直线xcos20º+ysin20º-3=0的倾斜角是

A、20⁰　　　 B、160⁰　　　 C、70⁰　　　　  D、110⁰

2、　曲线f(x,y) =0关于点（1，2）对称的曲线方程是

　 A、f(x-1,y-2)=0　　B、 f(x-2,y-4)=0　 C、f(1-x,2-y)=0　 D、f(2-x,4-y)=0

3、　点（3，1）和（-4，6）在直线3x-2y+a=0的两侧，则的取值范围是

A、<-7或>24　B、-7<<24　 C、=-7或=24 　 D、≥-7

4、　给出下列命题：①所有直线都存在斜率；②截距式直线方程不能表示的直线是与两坐标轴垂直的直线；③一般式直线方程可表示任何直线。其中正确命题的个数为

A、0　　　 B、1　　　　C、2　　　　  D、3

5、　点P(x,y)到x轴、y轴和直线x+y-2=0的距离都相等，则的值一定是

A、　　 B、　　C、　　  D、以上结论都不对

6、　直线l过点P(3,2)，与x轴、y轴的正半轴交于A、B两点，O是坐标原点，当△AOB面积最小时，直线的方程是

A、x-y-1=0　　B、x+y-5=0　　C、2x+y-12=0　　 D、3x+2y-13=0

7、直线ax+3y-9=0与直线x-3y+b=0关于原点对称，则a,br的值分别为

A、1，9　　　 B、-1，9　　　 C、1，-9　　　　　  D、-1，-9

8、若直线过点（1，1），且与两坐标轴所围成的三角形面积为2，则直线的条数是

A、1　　　　  B、2　　　　　 C、3　　　　　　　  D、4

9、过原点的直线交于两点，则直线的斜率的取值范围是

10、设常数m>0，椭圆x²-2mx+m²y²=0的长轴是短轴的2倍，则m等于

　  

11、设抛物线y=ax²(a>0)与直线y=kx+b(k0)有两个交点，其横坐标分别是 、，而直线y=kx+b与x轴交点的横坐标是，那么，，的关系是

A、=+　　B、　　C、　　D、=+

12、把椭圆绕它的左焦点按顺时针方向旋转，则所得新椭圆的准线方程是

A、　 B、　C、 D、

13、以

 C、　　  D、

14、点(1，2)且与曲线只有一个公共点的直线

A、不存在　　　　　 B、有两条　　　　  C、有三条　　　　D、有四条

15、若双曲线的实轴长、虚轴长、焦距成等差数列，则双曲线的离心率是

　 A、2　　　　　  B、3　　　　　 C、　　　　　 D、

16、椭圆内有一点P(-1，1)，F为右焦点，若椭圆上的点M使得MP+2MF的值最小，则点M为

17、双曲线中，被点P(2，1)平分的弦所在的直线方程是

　　A、8x-9y=7　　　B、8x+9y=25　　　C、4x-9y=6　　 D、不存在

18、抛物线上存在关于直线x+y=0对称的两点，则的取值范围是

　　A、　　　 B、　　  C、　　　 D、

19、已知直线m，n与平面的一个充分条件是

　 　　　　　　　B、

　 C、　　　　　　　 D、

20、在下列命题中，真命题是

A、若直线m，n都平行于平面，则m//n

B、设是直二面角，若直线m　

C、若直线m，n在平面内的射影依次是一个点和一条直线，且，则n在内或n与平行

D、设m，n为异面直线，若m与平面平行，则n与相交

21、等边△ABC的边长为，AD是BC边上的高，将△ABD沿AD折起，使之与△ACD所在平面成120⁰的二面角，这时A点到BC的距离是

A、　　　　B、　　　　 C、3　　　　 D、2

　　22、在正方体ABCD-A₁B₁C₁D₁中，M、N分别为棱AA₁和B₁B的中点，若为直线CM和ND₁所成的角，则cos等于

A、　　　　　 B、　　　　　 C、　　 D、

23、在下列命题中：

①与两条异面直线都相交的两条直线是异面直线

②直线上有两点到平面的距离相等，则此直线与平面平行

③二面角的棱垂直于二面角的平面角所在平面

④如果一个平面过另一个平面的斜线，那么这两个平面必不垂直

其中错误命题的个数为

A、1　　　 B、2　　　　C、3　　　　　D、4

　　 24、P为正四面体ABCD的面ABC内的一点，则在平面ABC内，过P且与棱CD所在直线成60⁰角的直线的条数是

　　　　A、1　　　 B、2　　　　C、3　　　　  D、4

　　 25、PA、PB、PC是从P点引出的三条射线，它们之间每两条的夹角都是60⁰，则直线PC与平面PAB所成的角是

　　　　A、45⁰　B、60⁰ 　 C、余弦值为的锐角　　 D、正切值为的锐角

二、　　　　　　 填空题（本大题共6小题，每小题3分，共18分）

26、等腰三角形两腰所在直线是和，底边过点（3，-8），则底边所在的直线方程是_____________________________。

27、已知，则的最小值是_____________________。

28、设平面外两点A和B到平面的距离分别为4cm和1cm，AB与平面成60⁰角，则线段AB的长为____________________________。

29、A是锐二面角的棱上一点，P是平面上的一点，PB⊥于B，PA与直线成45⁰角，PA与平面成30⁰角，则二面角的大小是________________。

30、椭圆_______________。

31、抛物线y²=2px(p>0)上一点M到它的准线距离为2，且M到此抛物线顶点的距离等于M 到它的焦点的距离，则此抛物线的焦点坐标是___________________。

三、　　　　　　 解答题（本大题共5小题，共32分。解答应写出文字说明、证明过程或演算步骤。）

32、过点A（3，-1）作直线交轴于B，交直线于点C，且∣BC∣=2∣AB∣，求直线的方程。

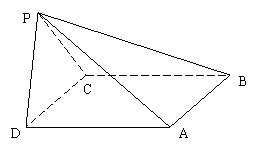33、如图，四棱锥P-ABCD中，侧 面PDC是边长为2的正三角形，且与底面垂直，底面ABCD是面积为的菱形，∠ADC为菱形的锐角。

（1）　　　 求证：PA⊥CD；

（2）　　　 求二面角P-AB-D的大小；

34、双曲线的中心在原点，焦点在x轴上，且过点(3，2)，又过左焦点且斜率为的直线交两条准线于M、N，以MN为直径的圆过原点，求双曲线的方程。

35、设椭圆的中心在原点O，一个焦点为F(0，1)，长轴和短轴的长度之比为t。

(1)求椭圆的方程；

(2)设经过原点且斜率为t的直线与椭圆在y轴右边部分的交点为Q，点P在该直线上，且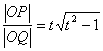，当t变化时，求点P的轨迹方程，并说明轨迹是什么图形。

36、已知椭圆C的斜率为是C上距离椭圆焦点F(1，)最近的点。

(I)、求椭圆C的方程；

(II)、若与圆相切的直线交椭圆于M、N两点，满足OM=ON(O是坐标原点)，求直线的方程。

高二年级第一学期期末综合测试题参考答案

一、选择题：

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
D	D	B	B	D	C	D	C	B	C	B	A	B	A	D
16	17	18	19	20	21	22	23	24	25
A	D	A	D	C	A	A	C	B	C

二、填空题：

 26、 　　　27、　　　　　　28、　

29、45⁰30、　　　31。

二、解答题：

32、

33、（1）略

　 （2）

　（3）

34、所求双曲线方程为：。

35、（1）椭圆方程为；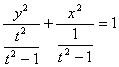

（2）点P的轨迹为抛物线在直线x= 右侧的部分和抛物线在直线左侧的部分。

36、(I)、所求的椭圆方程为：

　　 (II)所求的直线方程是