高二第二学期周末练习卷（一）

1、已知点A（5，2），B（－1，4），则线段AB的垂直平分线方程是 3x-y-3=0 ．

2、以A(2，2)、B(，-)、C(-2，-2)、D(-，)为顶点的四边形ABCD是 菱形 ．

3、已知直线过两点A(1，2)，B(m，3)，那么它的斜率与倾斜角分别是 ．

　。

4、直线x+y+1＝0的倾斜角是  ．

5、直线4x-5y+10=0的截距式方程是  ．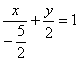

6、求直线xcos－y+1＝0(R)的倾斜角的取值范围  ．

7、已知平行四边形两条边所在直线的方程是x+y-1=0，3x-y+4=0，它的对角线的交点是M(3，3)，那么这个平行四边形其他两边所在直线的方程是 x+y-11=0,3x-y-16=0 ．

8、求过点A(1，)且倾斜角比直线x-2y+1=0的倾斜角大45的直线方程

是  ．

9、方程＝l(a>0，b>o)表示的直线的倾斜角是  ．　

10、已知直线和的斜率分别是方程6x+x-l=0的两个根，那么和的夹角

为  ．

11、已知直线ax+by+c=0，若ab<O且bc<O，则此直线不通过的象限是 第四象限 ．　

12、下列四个命题中，真命题是　　　　　　　　　　　　　　　　　　　 (　B )

　(A)经过定点P(x,y)的直线都可以用方程y-y=k(x-x)表示;

　(B)经过任意两个不同的点p(x，y)、p(x，y)直线都可以用(y-y)(x-x)=(x-x )(y-y)表示;

(C)不经过原点的直线都可以用方程y=kx+b表示；

(D)经过定点(0，b)的直线都可以用方程y=kx+b表示．

13、实数＝0是直线x-2ay=1与直线2x-2ay=1平行的　　　　　　　　　 （ A　）

　　(A)充要条件；　　　　　  (B)充分但非必要条件；

　　(C)必要但非充分条件；　　(D)既非充分又非必要条件．

14、若ABC的三个顶点的坐标分别是(2，2)、(-2，-2)、(2，-2)，则此三角形是 等边 三角形．

15、过点A（-5，3），且在X轴、Y轴上的截距相等的直线方程为 x+y+2=0或3x+5y=0 。

16、若点A、B的坐标分别为(cos，sin)、(cos2、sin2)，则A、B两点间距离等于  ．

17、已知直线被两直线：4x+y+6=0与：3x一5y一6＝0截得的线段中点为坐标原点，那么直线的方程是 x+6y=0 ．

18、到x轴的距离与到y轴的距离之比为3：4，且与两点A(1，2)、B(-3，4)等距离的点P的坐标为  和  ．

19、已知点P(1，1)、P(5，4)到直线的距离都等于2．直线的方程

为 3x-4y+11=0或3x-4y-9=0 或 7x+24y-81=0或x-3=0。

20、已知一直线过直线x-y-1＝0与直线2x-y-5=0的交点，且与两坐标轴围成的三角形的面积为8面积单位，则这条直线的方程是 x-4y+8=0或9x-4y-24=0 ．

21、直线经过点P（1，4），且在两坐标轴上的截距均为正数，当截距之和为最小值时的直线方程是 2x+y-6=0 ．

22、光线从点P（－2，1）发出经直线x-3y+2=0反射后，过点Q（3，5），则反射光线所在的直线的方程是 29x-22y+23=0 ．

23、已知两直线：(2+)x+y＝4+，:x-y+l＝O．求：

(1) 和的交点N的坐标；　　(2) 和的夹角．

　　　　　　　　　　　

24．过点M（2，1）的直线分别交x轴，y轴的正半轴于A,B两点。

（1）当AOB的面积S最小时，求直线的方程；（x+2y-4=0）

（2）当最小时，求直线的方程。　  (x+y-3=0)

25、已知直线：2x-3y+1=0, 求：

（1）点A（－1，－2）关于的对称点A的坐标；　　　  A

（2）直线m：3x-2y-6=0关于的对称直线m的方程。　 　(9x-46y+102=0)

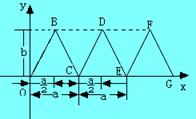
26、三角波是电学中常见的波形，试分别写出下图波形中线段OB、BC、CD、DE所在直线的方程．

OB:　 　 BC:　

CD:　

DE: