徽州一中2002—2003学年度高二数学单元测验(不等式)
命题:毕林裕
一、选择题
1.如果![]() 则下面四个命题中正确的命题是( )
则下面四个命题中正确的命题是( )
A.如果 a>b , c>b,那么a>c; B.如果 a>-b, 那么c-a<c + b
C.如果 a>b, 那么ac2>bc2; D.如果 a>b, c>d,那么ac>bd;
2. 不等式![]() 的解集为( )
的解集为( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
3.
a,b,c![]() , a>b是
, a>b是![]() 的
( ) 条件
的
( ) 条件
A.充分且必要 B.必要但不充分C.充分但不必要 D.既不充分又不必要
4.
若![]() 则下列不等式成立的是 ( )
则下列不等式成立的是 ( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
5.
若![]() 的取值范围是(
)
的取值范围是(
)
(A)[0,![]() ]
]![]() (B)[
(B)[![]() ,2
,2![]() ]
]![]()
(C)[![]() ,
,![]() ] (D)[
] (D)[![]() ,2
,2![]() ]
]![]()
6. 下列各式中最小值等于2的是 ( )
A. ![]() B.
B. 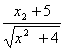 C.
C. ![]() D.
D. ![]()
7. 下列各组不等式中同解的是( )
A.x>6与x(x-3)2>6(x-3)2
B.![]() ≥0与x≥2
≥0与x≥2
C.x2-3x+3+![]() >
>![]() 与x2-3x+2>0
与x2-3x+2>0
D.![]() >0与x2-3x+2>0
>0与x2-3x+2>0
8..函数y=![]() (x>-1)的图象的最低点的坐标是( )
(x>-1)的图象的最低点的坐标是( )
A.(1,2) B.(1,-2) C.(0,2) D.不存在
9..集合M={x![]() <8x},N=
<8x},N=![]() ,则
,则![]() =( )
=( )
A.(0,![]() )
B.(
)
B.(![]() ,2) C.(1,
,2) C.(1,![]() ) D.
) D.![]()
10.某市用37辆汽车往灾区运送一批救灾物质,假设以v公里每小时的速度直达灾区,已知某市到灾区公路线长400公里,为了安全需要两汽车间距不得小于![]() 公里,那么,这批物质全部到达灾区的最短时间是( )
公里,那么,这批物质全部到达灾区的最短时间是( )
(A)![]() 小时 (B)12小时 (C)6小时 (D)24小时
小时 (B)12小时 (C)6小时 (D)24小时
11.使x-4+x-5<a有实数解的a为( )
A.a>1 B.1<a<9 C.a>1 D.a≥1
12.已知R1,R2是阻值不同的两个电阻,现分别按图(1)和图(2)连接,设相应的总阻值分别为RA,RB则RA和RB的大小关系是( )
|
|
|
|
|
|

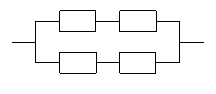
图(1) 图(2)
(A)RA>RB ; (B)RA=RB ; (C)RA<RB ;( D)不确定。
二、填空题,
13.关于x的不等式![]() 的解集为
的解集为![]() ,那么实数a的值为
。
,那么实数a的值为
。
14.设a>0, b>0 ,且2a+3b=1,则ab的取值范围是 。
15.如果一辆汽车每天行驶的路程比原来多19km,那么在8天内它的行程就超过2200km,
如果它每天的行程比原来少12km,那么它行驶同样的路就得花9天多时间,这辆汽车原来每天行程的千米数满足 。
16.已知三个不等式①ab﹥0;②-![]() ﹤-
﹤-![]() ;③bc﹥ad以其中两个做条件,余下一个做结论,则可以组成
个正确命题.
;③bc﹥ad以其中两个做条件,余下一个做结论,则可以组成
个正确命题.
三、解答题(本大题解答应写出文字说明,证明过程式或推演步骤)
17.如果![]() ,试比较ab,
,试比较ab,![]() ,
, ![]() 的大小。
的大小。
18解不等式:![]() <-1
<-1
19.设f(x)=log3(![]() )
)
(1)求证:f(x)的定义域为![]() ;
;
(2)求证:f(x)是减函数;
(3)求![]() 的取值范围(a
的取值范围(a![]() R)
R)
20.某商品进货价每件50元,据市场调查,当销售价格(每件x元)在50≤x≤80时,每天售出的每件数P=![]() ,若想每天获得的利润最多,销售价格每件应定为多少元?
,若想每天获得的利润最多,销售价格每件应定为多少元?
21.已知函数y=loga(a2x)![]() (ax) (a﹥0且a≠1)的最小值是-
(ax) (a﹥0且a≠1)的最小值是-![]() ,最大值是0,其定义域恰是不等式4x-1-5·2x+16≤0的解,求a的值.
,最大值是0,其定义域恰是不等式4x-1-5·2x+16≤0的解,求a的值.
答案:
一.选择题:B D B C C D A C C B C B
二.13。![]() ; 14。
; 14。![]() ; 15。(256,260); 16。3;
; 15。(256,260); 16。3;
三.17。ab≤![]() ≤
≤![]()
18.(-1,1)∪(2,3)
19.1)略;2)略;3)![]()
20.每件60元时,每天获利最多,最多是2500元。
21.a=![]()
