高中学生学科素质训练
新课程高二上学期数学
期末考试卷
一、选择题:本大题共10小题;每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.![]() 是方程
是方程 ![]() 表示椭圆或双曲线的 ( )
表示椭圆或双曲线的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.不充分不必要条件
2.圆C切![]() 轴于点M且过抛物线
轴于点M且过抛物线![]() 与
与![]() 轴的两个交点,O为原点,则OM的长是 ( )
轴的两个交点,O为原点,则OM的长是 ( )
A.4 B.![]() C.
C.![]() D.2
D.2
3.与曲线![]() 共焦点,而与曲线
共焦点,而与曲线![]() 共渐近线的双曲线方程为 ( )
共渐近线的双曲线方程为 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
4.若抛物线![]() 与圆
与圆![]() 有且只有三个公共点,则
有且只有三个公共点,则![]() 的取值范围是 ( )
的取值范围是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.抛物线![]() 上有一点P,P到椭圆
上有一点P,P到椭圆![]() 的左顶点的距离的最小值为( )
的左顶点的距离的最小值为( )
A.![]() B.2+
B.2+![]() C.
C.![]() D.
D.![]()
6.若椭圆![]() 与双曲线
与双曲线![]() 有相同的焦点F1、F2,P是两曲线的一个交点,则
有相同的焦点F1、F2,P是两曲线的一个交点,则![]() 的面积是 ( )
的面积是 ( )
A.4 B.2 C.1 D.![]()
7.一个圆的圆心为椭圆的右焦点,且该圆过椭圆的中心交椭圆于P,直线PF![]() (F
(F![]() 为椭圆的左焦点)是该圆的切线,则椭圆的离心率为 ( )
为椭圆的左焦点)是该圆的切线,则椭圆的离心率为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.圆心在抛物线![]() 上,且与
上,且与![]() 轴和该抛物线的准线都相切的一个圆的方程是( )
轴和该抛物线的准线都相切的一个圆的方程是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
9.当![]() 时,方程
时,方程![]() 的解的个数是 ( )
的解的个数是 ( )
A.0 B.1 C.2 D.3
|
二、填空题:本大题共4小题;每小题4分,共16分,把答案填在题中横线上.
11.若曲线![]() 的焦点为定点,则焦点坐标是 .
的焦点为定点,则焦点坐标是 .
12.设圆过双曲线![]() 的一个顶点和一个焦点,圆心在此双曲线上,则圆心到双曲线中心的距离为
.
的一个顶点和一个焦点,圆心在此双曲线上,则圆心到双曲线中心的距离为
.
13.已知椭圆![]() 与双曲线
与双曲线![]() (
(![]() )有相同的焦点F1、F2、P是两曲线的一个交点,则
)有相同的焦点F1、F2、P是两曲线的一个交点,则![]() 等于 .
等于 .
14.对于椭圆![]() 和双曲线
和双曲线![]() 有下列命题:
有下列命题:
①椭圆的焦点恰好是双曲线的顶点;
②双曲线的焦点恰好是椭圆的顶点;
③双曲线与椭圆共焦点;
④椭圆与双曲线有两个顶点相同.
其中正确命题的序号是 .
三、解答题:本大题共6小题;共54分.解答应写出文字说明,证明过程或演算步骤.
15.(本小题满分8分)已知圆c关于![]() 轴对称,经过抛物线
轴对称,经过抛物线![]() 的焦点,且被直线
的焦点,且被直线![]() 分成两段弧长之比为1:2,求圆c的方程.
分成两段弧长之比为1:2,求圆c的方程.
16.(本小题满分9分)已知直线![]() 与圆
与圆![]() 相切于点T,且与双曲线
相切于点T,且与双曲线![]() 相交于A、B两点.若T是线段AB的中点,求直线
相交于A、B两点.若T是线段AB的中点,求直线![]() 的方程.
的方程.
17.(本小题满分9分)已知椭圆的一个顶点为A(0,-1),焦点在x轴上.若右焦点到直线![]() 的距离为3.
的距离为3.
(1)求椭圆的方程;
(2)设椭圆与直线![]() 相交于不同的两点M、N.当
相交于不同的两点M、N.当![]() 时,求m的取值范围.
时,求m的取值范围.
18.(本小题满分9分)双曲线![]() 的右支上存在与右焦点和左准线等距离的点,求离心率
的右支上存在与右焦点和左准线等距离的点,求离心率![]() 的取值范围.
的取值范围.
19.(本小题满分9分)已知圆![]() 和抛物线
和抛物线![]() 上三个不同的点A、B、C.如果直线AB和AC都与圆O相切.求证:直线BC也与圆O相切.
上三个不同的点A、B、C.如果直线AB和AC都与圆O相切.求证:直线BC也与圆O相切.
20.(本小题满分10分)A、B、C是我军三个炮兵阵地,A在B的正东方向相距6千米,C在B的北30°西方向,相距4千米,P为敌炮阵地.某时刻,A发现敌炮阵地的某信号,由于B、C比A距P更远,因此,4秒后,B、C才同时发现这一信号(该信号的传播速度为每秒1千米).若从A炮击敌阵地P,求炮击的方位角.
高中学生学科素质训练
新课程高二上学期数学
期末考试参考答案
一、1.B; 2.D; 3.A; 4.D; 5.A; 6.C; 7.C; 8.D; 9.D; 10.A;
二、11.(0,±3); 12.![]() ; 13.
; 13.![]() ; 14.①②
; 14.①②
三、15.设圆C的方程为![]()
![]() 抛物线
抛物线![]() 的焦点F(1,0)
的焦点F(1,0) ![]()
①………………………………………………3分
又直线![]() 分圆的两段弧长之比为1:2,可知圆心到直线
分圆的两段弧长之比为1:2,可知圆心到直线![]() 的距离等于半径的
的距离等于半径的![]()
即![]() ②………………………………………………5分
②………………………………………………5分
解①、②得![]() 故所求圆的方程为
故所求圆的方程为 ![]() ……………………8分
……………………8分
16.直线![]() 与
与![]() 轴不平行,设
轴不平行,设![]() 的方程为
的方程为 ![]() 代入双曲线方程 整理得
代入双曲线方程 整理得
![]() ……………………2分 而
……………………2分 而![]()
![]() ,于是
,于是
![]() 从而
从而![]() 即
即 ![]() ……4分
……4分
![]() 点T在圆上
点T在圆上 ![]() 即
即![]() ①
①
由圆心![]() .
.![]() 得
得 ![]() 则
则 ![]() 或
或 ![]()
当![]() 时,由①得
时,由①得 ![]() 的方程为
的方程为 ![]() ;
;
当![]() 时,由①得
时,由①得 ![]()
![]() 的方程为
的方程为![]() .故所求直线
.故所求直线![]() 的方程为
的方程为![]() 或
或 ![]() …………………………8分
…………………………8分
17.(1)依题意可设椭圆方程为 ![]() ,则右焦点F(
,则右焦点F(![]() )由题设
)由题设
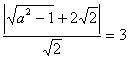 解得
解得![]() 故所求椭圆的方程为
故所求椭圆的方程为![]() .
.
![]() ………………………………………………3分.
………………………………………………3分.
(2)设P为弦MN的中点,由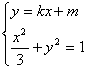 得
得 ![]()
由于直线与椭圆有两个交点,![]() 即
即 ![]() ①………………5分
①………………5分
![]() 从而
从而![]()
![]() 又
又![]() ,则
,则
![]() 即
即 ![]() ②…………………………7分
②…………………………7分
把②代入①得 ![]() 解得
解得 ![]() 由②得
由②得 ![]() 解得
解得![]() .故所求m的取范围是(
.故所求m的取范围是(![]() )……………………………………9分
)……………………………………9分
18.设M![]() 是双曲线右支上满足条件的点,且它到右焦点F2的距离等于它到左准线的距离
是双曲线右支上满足条件的点,且它到右焦点F2的距离等于它到左准线的距离![]() ,即
,即![]() ,由双曲线定义可知
,由双曲线定义可知  ……4分
……4分
由焦点半径公式得
![]()
![]() …………………………6分
…………………………6分
而![]() 即
即 ![]() 解得
解得![]() 但
但 ![]() ……………………………………9分
……………………………………9分
19.设![]() ,
,![]() 则
则
AB的方程为 ![]()
BC的方程为 ![]()
AC的方程为 ![]() ……………………………………3分
……………………………………3分
![]() 为圆的切线,有
为圆的切线,有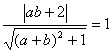 即
即![]() 同理
同理
![]() 、
、![]() 为方程
为方程![]() 的两根,则
的两根,则
![]() ………………………………………………8分
………………………………………………8分
于是圆心到直线BC的距离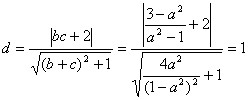 故BC也与圆O相切。
故BC也与圆O相切。
…………………………………………10分.
20.以线段AB的中点为原点,正东方向为![]() 轴的正方向建立直角坐标系,则
轴的正方向建立直角坐标系,则![]() 依题意
依题意 ![]()
![]() 在以A、B为焦点的双曲线的右支上.这里
在以A、B为焦点的双曲线的右支上.这里![]() .其方程为
.其方程为 ![]() ……3分
……3分
又 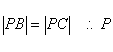 又在线段AB的垂直平分线上
又在线段AB的垂直平分线上![]() ………………5分
………………5分
由方程组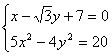 解得
解得  即
即 ![]() …………8分
…………8分
由于![]() ,可知P在北30°东方向.………………………………………………10分
,可知P在北30°东方向.………………………………………………10分