高中学生学科素质训练

新课程高二下学期数学

期中考试卷

一、选择题：本大题共10小题；每小题3分，共30分. 在每小题给出的四个选项中，只有

一项是符合题目要求的.

1．下列说法正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．直线a平行于平面M，则a平行于M内的任意一条直线

　　　 B．直线a与平面M相交，则a不平行于M内的任意一条直线

　　　 C．直线a不垂直于平面M，则a不垂直于M内的任意一条直线

　　　 D．直线a不垂直于平面M，则过a的平面不垂直于M

2．若a、b是两条异面直线，则存在唯一确定的平面β满足　　　　　　　　　　　　　　　　　　（　　）

　　　 A．a//β且b//β　　　 B．aβ且b//β　　　C．a⊥β且b⊥β　　D．aβ且b⊥β

3．设P是平面α外一点，且P到平面α内的四边形的四条边的距离都相等，则四边形是（　　）

　　　 A．梯形　　　　　　　　　 B．圆外切四边形　　 C．圆内接四边形　　 D．任意四边形

4．三棱锥成为正三棱锥的充分而不必要条件是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．各侧面与底面所成的角相等　　　　　　　 B．各侧面是全等的等腰三角形

　　　 C．高通过底面外心，且底面是正三角形 D．四个面均为正三角形

5．已知AB是异面直线a、b的公垂线段，AB=2，且a与b成30°角，在直线a上取AP=4，

则点P到直线b的距离为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

A．　　　　　　　　　B．4　　　　　　　　　　　　C．2　　　　　　　　D．或2

6．平面α与正四棱柱的四条侧棱AA₁、BB₁、CC₁、DD₁分别交于E、F、G、H.若AE=3，

BF=4，CG=5，则DH等于　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

A．6　　　　　　　　　　　　B．5　　　　　　　　　　　　C．4　　　　　　　　　　　　D．3

7．二面角α—EF—β是直二面角，C∈EF，AC α，BCβ,∠ACF=30°,∠ACB=60°，

则cos∠BCF等于　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

A．　　　　　　　　 B．　　　　　　　　　 C．　　　　　　　　　 D．

8．正四棱锥的底面边长为3，体积为，则它的相邻两个侧面所成角的余弦值为（　　）

　　　 A．　　　　　　　　　 B．　　　　　　　　C．　　　　　　　　　 D．

9．长方体的对角线长为2，则其全面积的最大值为　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　　　　　　B．　　　　　　　　　C．4　　　　　　　　　　　　D．8

10．一个球与正三棱柱的三个侧面和两个底面都相切，已知球的体积为，那么该三棱

柱的体积为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

A．16　　　　　　　　B．24　　　　　　　　 C．48　　　　　　　　D．96

二、填空题：本大题共4小题；每小题4分，共16分，把答案填在题中横线上.

11．若异面直线a、b所成的角为60°,P是空间一点,则过点P且与a、b所成的角都是40°

的直线的条数是　　　　　　　 .

12．边长为2的正方形ABCD在平面α内的射影是EFCD，如果AB与平面α的距离为，

则AC与平面α所成角的大小是　　　　　　　　 .

13．球的半径为18，经过球面上一点作一个平面，使它与经过这点的半径成45°角，则这
个平面截球的截面面积为　　　　　　　 .

14．三棱锥S—ABC中，SA⊥BC，SA=BC=a，SA与BC的距离为b，则三棱锥的体积为

　　　　　　　　　　.

三、解答题：本大题共6小题；共54分，解答应写出文字说明、证明过程或演算步骤.

15．（本小题满分7分）已知AB是异面直线a、b的公垂线，a⊥平面α，b⊥平面β，

α∩β=c，求证：AB//c.

16．（本小题满分7分）已知α—AB—β是二面角，aα，bβ，a、b与AB都不垂直.

①求证：a与b必不垂直；

②若a与β、b与α所成的角都是45°，求a与b所成角的大小.

17．（本小题满分10分）已知四棱锥S—ABCD中，底面为正方形，SA⊥底面ABCD，且

AB=SA=a，M、N分别是AB、SC的中点.　　 ①求证：AB⊥MN；

②求证：MN是异面直线AB与SC的公垂线；　③求二面角B—SC—D的大小.

18．（本小题满分10分）已知VC是△ABC所在平面的一条斜线，点N是V在平面ABC内

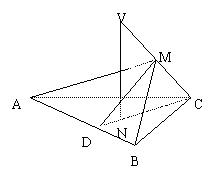的射影，且在△ABC的高CD上，AB=a，VC与AB之间的距离为h，点M∈VC.

①证明：∠MDC是二面角M—AB—C的平面角；

②当∠MDC=∠CVN时，证明：VC⊥平面AMB；

③若∠MDC=∠CVN=θ.（，

求四面体MABC的体积.

19．（本小题满分10分）已知直三棱柱ABC—A₁B₁C₁中，B₁C₁=A₁C₁，AC₁⊥A₁B. M、N分

别为A₁B₁、AB的中点.

①求证：平面AMC₁//平面NB₁C；

②求A₁B与B₁C所成的角的大小；

③若A₁C₁=AA₁=1，∠A₁C₁B₁=90°求三棱柱ABC—A₁B₁C₁的体积.

20．（本小题满分10分）某企业要设计一个下部是圆柱形，上部是半球形的密闭容器，容积

为常量V，问当圆柱的底面半径与圆柱的高为何值时，制造这个密闭容器的用料最省（即

容器的表面积最小）.

高中学生学科素质训练

新课程高二下学期数学参考答案

期中考试卷

一、1.B　2.B　3.B  4.D　5.A　6.C  7.D　8.C　9.D  10.C

二、11．2；　12.　30° 13. 162π　14. a²b

三、15．过AB、a作平面γ交平面α于直线d，过AB、b作平面δ交平面β于直线e，

∵a⊥平面α　∴a⊥d　 又a⊥ABγ　 ∴AB//a　　同理AB//e

∴d//e而c、eβ　 ∴d//c　 故AB//C…………………………………………………………7分

16．①假设a⊥b，由于b是β内任意一条直线，则a⊥β　又α⊥β，∴a⊥AB　这和a与AB不垂直矛盾

　　故假设不成立，则a与b必不垂直……………………………………………………………………3分

②设a与b所成的角为θ，由　　∴θ=60°

即a与b所成的角为60°………………………………………………………………………………7分

17．①连AC并取AC的中点O，连OM、ON，∵N为SC的中点，∴NO//SA　而SA⊥底面ABCD

　　∴NO⊥底面ABCD　又M为AB的中点，∴OM⊥AB 故MN⊥AB………………………………3分

②连结SM、CM，则SM=CM=　N为SC的中点，

∴MN⊥SC　　又MN⊥AB（已证） 故MN是异面直线AB与SC的公垂线……………………6分

③在平面SBC内作BE⊥SC，E为垂足，连结DE.　在△EBC和△EDC中，BC=CD=a，CE=CE

∠BCE=∠DCE　∴△EBC≌△EDC　于是∠BEC=∠DEC=90°　即DE⊥SC　则∠BED为二面角

B—SC—D的平面角. 连结BD，在△BDE中，BD=a　BE=DE=，由余弦定理得

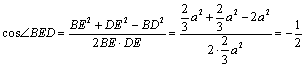　　  ∴∠BED=120°

即二面角B—SC—D为120°…………………………………………………………………………10分

18．①由已知，CD⊥AB，VN⊥平面ABC，N∈CD，AB平面ABC　∴VN⊥AB，∴AB⊥平面VNC

又V、M、N、D都在VNC所在的平面内.所以DM与VN必相交，且AB⊥DM，AB⊥CD

∴∠MDC为二面角M—AB—C的平面角……………………………………………………………4分

②由已知，∠MDC=∠CVN，在△VNC和△DMC中　∠NCV=∠MCD，又∵∠VNC=90°，

∠DMC=∠VNC=90°　故有DM⊥VC又AB⊥VC　 ∴VC⊥平面AMB………………………7分

③由①②可知DM⊥AB，DM⊥VC且D∈AB，M∈VC　∴DM=h，又∠MDC=θ，在Rt△MDC中，CM=h·tanθ　∴V_{四面体MABC}=V_{三棱锥C—ABM}=·CM·S_△ABM=h·tanθ·…10分

19．①∵CN//C₁M，AM//B₁N　∴平面AMC₁//平面NB₁C………………………………………………2分

②∵B₁C₁=A₁C₁，M为A₁B₁的中点，∴C₁M⊥A₁B₁　而ABC—A₁B₁C₁为直三棱柱，∴C₁M⊥平面

ABB₁A₁　∴AM为AC₁在平面ABB₁A₁内的射影　又AC₁⊥A₁B　∴A₁B⊥AM　而AM//B₁N

∴A₁B⊥B₁N　同理CN⊥平面ABB₁A₁　故A₁B⊥B₁C　即A₁B与B₁C所成的角为90°………6分

③当A₁C₁=A₁A=1，∠A₁C₁B₁=90°时，V_ABC—A1B1C1=S_△A1B1C1·AA₁=………………………10分

20．设圆柱的底面半径为R，高为h，由题设得πR³+πR²h=V　∴h=………………3分

这时容器的表面积S=2πR²+2πRh+πR²=3πR²+2πR（）…………………………5分

=3πR²+…………8分

当且仅当，即R=时，上式等号成立，这时h=.

故当圆柱的底面半径与高都等于时，容器的用料最省…………………………………………10分