高二数学综合训练（三）

　　　　　  班级＿＿＿＿　　　姓名＿＿＿＿＿＿＿

一、选择题：

1．灯泡使用时数在1000小时以上的概率为0．2，则3只这样的灯泡在使用l000小时后坏了一只的概率是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　)

（A）0．128　　　　  (B)0．1384　　　　　  (C)O．032　　　　  (D)0．096

2．用0，1，2，3，4组成没有重复数字的全部五位数中，若按从小到大的顺序排列，则数字12340应是第几个数。　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　 ）

　 A、6　　　　　 B、9　　　　　 C、10　　　　  D、8　

3．AB和CD为平面内两条相交直线，AB上有m个点，CD上有n个点，且两直线上各有一个与交点重合，则以这m+n-1个点为顶点的三角形的个数是　　　　　　　　　　　　　　　　　　　　　　 （　 ）

　 B、　C、　　D、

4．若(1-2x)⁵的展开式中，第2项小于第1项，且不小于第3项，则的取值范围是　　　　　 （　 ）

（A）x＜-　　　 （B）-＜x＜0　　　　（C）-≤x＜　　　 （D）-≤x≤0

5．α、β表示平面，l表示既不在α内也不在β内的直线，存在以下三个事实　①l⊥α；　 ②l∥β；

③α⊥β. 若以其中两个为条件，另一个为结论，构成命题，其中正确命题的个数为　　 　　（　 ）

　　 A．0个　 　　　　 B．1个　 　　　　C．2个　　　　　　　 D．3个

6．已知二面角α—AB—β的平面角是锐角θ，α内一点C到β的距离为3，点C到棱AB的距离为4，那么tanθ的值等于　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　 ）

A．　　　　　　  B．　　　　　 　　 C．　　　　　　　　  D．

7．先后三次投掷一枚均匀的硬币，至少出现一次正面的概率是　　　　　　　　　　　　　　　 (　　)

　 （A） 　　　　　　　 （B）　　　　　  （C）　　　　　　 （D）

8．函数y＝2x³—3x²—12x＋5在[0，3]上最大、小值分别是　　　　　　　　　　　　　　　　  (　　)

(A)5，一15　　　　　 (B) 5，4　　　　　　 (C)一4、一15　　　　 (D)5，一16

9．若二次函数＝ax²＋c在区间(0，十∞)内单调递增，则a，c应满足　　 　　　　　　( 　 )

　　(A)a＜0，c＝0　 　　(B)a＞0，c∈R　　　 　(C)a＜0，c∈R　　　　(D)a＞0，c≠0

10．两个平行于圆锥底面的平面将圆锥的高分成相等的三段，那么圆锥被分成的三部分的体积的比是（　）

　（A）1∶2∶3　　　　　 （B）1∶7∶19　　　　　 （C）3∶4∶5　　　　 （D）1∶9∶27

11．某村有旱地和水田若干，现需要估计平均亩产量，用按5％分层抽样的方法抽取15亩早地45亩水田进行调查，则这个村的早地与水田的亩数分别为 　　　　　　　　　　　　　　　　　　　　　(　　)

　(A)150，450　　　　　  (B)300，900　　　　　  (C)600，600　　　　  (D)75，225

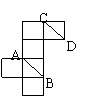12．将正方体的纸盒展开（如图），直线AB，CD在原正方体中的位置关系是　　　　　　　　　　　　　　　　 　（　 ）

　　　　 A．平行　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B．垂直

　　　　 C．相交且成60°角　　　　　　　　　　　　　　　　　　　　　　　　D．异面且成60°角

二、填空题：把答案填在题中横线上

13．曲线y＝x³十x²十2在点(—1，2)处的切线方程为＿＿＿＿＿＿

14．将一枚均匀硬币连掷5次，如果出现次正面的概率等于出现十1次正面的概率，那么＝＿＿

15． (tgx+ctgx)²ⁿ的展开式中，含tg²x项的系数是______。

16． P、Q是半径为R的球面上的两点，它们的球面距离是，则过P、Q的平面中，与球心的最大距离是

三、解答题：解答应写出文字说明，证明过程或演算步骤

17．将一枚均匀硬币抛掷5次，

(1)求第一次、第四次出现正面，而另外三次都出现反面的概率；

　　(2)求两次出现正面。三次出现反面的概率．

　　

18．下表给出了某校120名12岁男孩身高的资料．

身高	[122，126）	[126，130）	[130，134）	[134，138）	[138，142)
人数	5	8	10	22	33
身高	[142，146]	[146，150）	[150，154)	[154，158)
人数	20	11	16	5

　  (1)列出样本的频率分布表并画出直方图．

　　(2)根据上述抽样结果，估计本校同龄男孩身高在134～146cm的概率有多大?

　

19．已知二面角α—l—β等于θ，PA⊥α，PB⊥β，A、B为垂足，若PA=m，PB=n，求P到棱l的距离.

20、若某一等差数列的首项为，公差为的常数项，其中m是－15除以19的余数，则此数列前多少项的和最大？并求出这个最大值。

21．矩形ABCD的两个顶点A、B在x轴上，另两个顶点C、D在抛物线y=4－x²位于x轴上方的曲线上，求矩形ABCD的面积最大值。

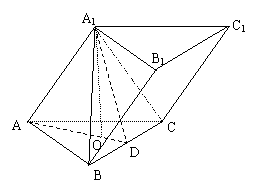22.斜三棱柱ABC-A₁B₁C₁的底面是边长为2的正三角形，顶点A₁在底面的射影O是△ABC的中心，异面直线AB与CC₁所成的角为45°.

(1)　 求证：AA₁⊥平面A₁BC；

(2)　 求二面角A₁－BC-A的平面角的正弦值；

(3)　 求这个斜三棱柱的体积.

高二数学综合训练（三）答案

　　　　　 

一、选择题：DCDBC　　DCABB　 BD

二、填空题： 13． x－y＋3=0　　　14． ＝2　　　 15． C　　　 16．

三、解答题

 17．

 解　(1)设第i次抛掷硬币出现正面事件记为A_i，表示第i次抛掷硬币出现反面的事件(i＝1，2，3，4，5)，根据题意知A_i与都是相互独立事件，且P(A_i)＝P()＝．　　　

 第一次、第四次出现正面，另外三次出现反面的事件为A₁A₄。

 则P(A₁A₄)＝P(A₁)P()P()P(A₄)P()＝P((A₁)×P()×P()×P(A₄)×P()＝××××=。

 答：第一次、第四次出现正面，另三次出现反面概率为．

 (2)由于每次抛掷出现正面的概率是相同的，所以两次出现正面，三次出现反面的事件就是五次独立重复试验中，正面恰好出现两次．根据n次独立重复试验中某个事件发生n次的概率公式，得所求的概率为P₅(2)＝　　　　　　　　 

答；两次出现正面，三次出现反面概率为．　　　　

18．

　[解]　(1)频率分布表如下：

身高	[122，126)	[126，130)	[130，134)	[134。138]	[138，142]	[142，146	[146，150]	[150，154]	[154，158)
人数	5	8	10	22	33	20	11	6	5
频率

　  (2)频率分布直方图如图

　  (3)因为样本中身高在134～146cm的频率为十十＝0．625

　　所以本校同龄男孩身高在134～146cm的概率约为0．625。

[点拨]　这是第二种类型的总体分布，由于组距、分点巴定，故各组的频率可求。其中　134～146cm学生有3组，这三组的频率和就是身高在134～146cm的频率，用它可以估计相应概率．

19．

解：在平面α内作AC⊥l于C，连结BC、PC.α，l⊥AC，∴l⊥PC即PC是P到l的距离.

≠

∵PB⊥β，lβ，l⊥PC，∴l⊥BC. 即∠ACB为二面角α—l—β的平面角，∠ACB=θ，

∵l⊥AC，l⊥PC，l⊥BC，  ∴PACB是一个平面四边形. 又∠PAC=∠PBC=90°，∴四边形PACB内

接于以PC为直径的圆，∠APB=π－θ.　在△APB中，由余弦定理，得 AB²=PA²+PB²－2PA·PBcos

∠APB=m²+n²+2mncosθ.　由正弦定理，得，即为所求P到

l的距离.

20、

解：由已知得：。

注意到，从而等差数列的通项公式是：，设其前k项之和最大，则

，解得k=25或k=26，故此数列的前25项之和与前26项之和相等且最大，。

21．x=　S=

(4)　 22.

(1)　 由已知可得A₁-ABC为正三棱锥，∠A₁AB=45°

∴∠AA₁B=∠AA₁C=90°即AA₁⊥A₁B,AA₁⊥A₁C

∴AA₁⊥平面A₁BC

(2)　 连AO并延长交BC于D,则AD⊥BC，连A₁D,

则∠ADA₁为所求的角。由已知可得 AD＝Absin60°＝,

AA₁=Absin45°=,∴sin∠ADA₁=

(3)　 在Rt△AA₁D中，A₁D=∴A₁O=

∴V_柱＝S_△ABC·A₁O=·4·sin60°·.