高二期末数学综合训练（二）
班级＿＿＿＿＿＿ 姓名＿＿＿＿＿ 学号＿＿＿＿＿＿
一、选择题：
1．一袋中装有5只白球，3只黄球，在有放回模球中，用A1表示第一次模得白球，A2表示第二次模得白球，则事件A1与
是
（ ）
(A)相互独立事件 (B)不相互独立事件 (C)互斥事件 (D)对立事件
2．不同的五种商品在货架上排成一排，其中甲、乙两种必须排在一起，丙、丁两种不能排在一起，则不同的排法种数共有 ( )
A、12种 B、20种 C、24种 D、48种
3、半径为R的两个球，一个球的球心在另一个球的球面上，则两球的交线圆的周长为 ( )
A．
B．
C 
D．2
4．若
（ ）
A 1 B 
C 
D 
5．在
的展开式中
的系数为
（ ）
A 160 B 240 C 360 D 800
6．在棱长为1的正方体ABCD－A1B1C1D1的底面A1C1取一点E，使AE与AB、AD所成的角都是
，则线段AE的长为
( )
（A）
（B）
（C）
（D）
7．在三棱锥A—BCD中，AB=AC=AD，BC=1，∠ABC=∠BCD，∠BDC=
，∠ABD=
，则AC的长为 （ ）
A．1
B．
C．
D．
8. 用0，1，2，3，4，5六个数字组成无重复数字且能被25整除的六位数，共能组成这样 的六位数的个数是 ( )
A．42 B．36 C．24 D．18
9．对总数为N的一批零件随机抽取一个容量为30的样本，若每个零件被拙取的概率为0．25，则N= ( )
(A)150 (B)200 (C)120 (D)100
10.设
＝2x2—x3，则的单调递减区间是
( )
(A)(0，
) (B)( ，＋∞) (C)(—∞，0) (D)(—∞，o)和(，＋∞)
11．函数＝2x3—3x2十a的极大值为6，那么a的值等于
( )
(A)6 (B)0 (C)5 (D)1
12.正四棱锥每两条相邻侧棱所成的角都是
，侧棱长为
，则它的体积是
（ ）
（A）
（B）
（C）
（D）
二、填空题：把答案填在题中横线上
13．一袋中装有只黑球，
只白球，它们大小相同，编号不同，现在把球随机地一只一只摸出来，第
次(1≤≤+)模出的球是黑球的概率为_________．
14、
的展开式中
的系数为__________（用数字作答）。
15.曲线y＝x3—3x上切线平行于x轴的切点的坐标是＿)＿＿＿＿＿
16．一个球的外切正方体的表面积是6，则球的体积是＿＿＿＿
三、解答题：解答应写出文字说明，证明过程或演算步骤
17、用分层抽样法从10名男生5名女生中抽取3人参加智力游戏．试求某一男生甲以及某—女生乙分别被抽到的概率。
18．已知P、Q、M分别是45°的二面角α—l—β的面α、β和棱l上的点，直线MQ是直线PQ在β上的射影（如图），若PQ和β成
角，l和MQ成θ角，PM=a，求PQ的长.
19.某人连续射靶1 20次，其中射中5环4次，6环6次，7环30次，8环40次．，9环30次，10环10次，若射中某环的频率低于10％则视为发挥失常或超水平发挥．试估计此人能正常发挥时的概率．
20、（本小题满分12分）求证：
能被25整除。
21．己知函数＝x3—3x2＋2
(1)写出函数的单调区间；
(2)讨论函数的极大值和极小值，如有，试写出极值．
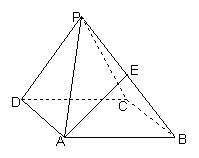
22.如图所示，正四棱锥P—ABCD中，侧棱PA与底面ABCD所成角的正切值为
.
（Ⅰ）求侧面PAD与底面ABCD所成二面角的大小；
（Ⅱ）若E是PB中点，求异面直线PD与AE所成角的正切值；
（Ⅲ）在侧面PAD上寻找一点F，使EF⊥侧面PBC. 试确定F点的位置，并加以证明.
高二数学综合训练（二）答案
一、选择题：ACBAB CCACD AA
二、填空题：
13． （
）
14、179
15. (－1,2) (1,－2)
16． 
17、 解∵抽样比为
∴抽取男生×10＝2人 抽取女生× 5＝l人
∴某男生甲被抽到的概率为P1＝
＝
某女生乙被抽到的概率为P2＝
18. 解 列出频率分布表如下
| 试验结果 | 频数 | 频率 |
| 5环 | 4 | 0．033 |
| 6环 | 6 | 0．05 |
| 7环 | 30 | 0．25 |
| 8环 | 40 | 0．333 |
| 9环 | 30 | 0．25 |
| 10环 | 10 | O．083 |
其中，5环，6环，10环射中的频率低于1％．
正常发挥水平的频率为0．25十O．333十0．25=0．833．
故此人能正常发挥水平的概率约为0．833．
19．
解:作PH⊥β于H，∵MQ是PQ在β上的射影，∴H在MQ上.作HN⊥l于N，并连结PN，由三垂直线定理可知PN⊥l， ∴∠PNH是二面角α—l—β的平面角，即∠PNH=45°.
设PQ=x，则NH=PH=xsin，
，MN=NH·cotθ=xsin·cotθ.
在Rt△PMN中，∵PM2=PN2+MN2，
，故
20、注意到
即可。
21． ①（－∞，0） （2，＋∞）↗，（0，2）↘，②x=0时，大2 x=2 时，小－2；
22.
解：（Ⅰ）连结AC，BD交于O，连结PO.∵P—ABCD为正四棱锥，
∴PO⊥底面ABCD.作PM⊥AD于M，连结OM，∴OM⊥AD.
∴∠PMO为侧面PAD与底面ABCD所成二面角的平面角.∵PO⊥底面ABCD，∴∠PAO为PA与底面ABCD所成的角. 
，即侧面PAD与底面ABCD所成的二面角为60°
（Ⅱ）连结EO，∵E为PB的中点，O为BD的中点，∴EO∥PD. ∴∠AEO为异面直线AE与PD所成角 在
由AO⊥截面PDB，可知AO⊥EO. 在Rt△AOE中
.
即异面直线AE与PD所成角的正切值是
（Ⅲ）延长MO交BC于N，连结PN，取PN中点G，连结EG，MG. ∵P—ABCD为正四棱锥且M为
AD的中点，∴N为BC中点. ∴BC⊥NM，BC⊥PN. ∴BC⊥平面PMN. ∴平面PMN⊥平面PBC.
∵PM=PN，∠PMN=60°，∴△PMN为正三角形. ∴MG⊥PN. ∴MG⊥平面PBC. 取AM中点为F，连结FE，则由EG∥MF且GE=MF得到MFEG为平行四边形，∴FE∥MG. ∴FE⊥平面PBC