高二数学期末综合训练一(第二学期新课程卷)
一、选择题:
1.5人站成一排,其中A不在左端也不和B相邻的排法种数为 ( )
A、48 B、54 C、60 D、66
2.曲线y=xn在x=2处的导数为12,则n为 ( )
(A)1 (B)2 (C)3 (D)4
3.半径为1的球面上有A、B、C三点,A与B、A与C之间的球面距离都是![]() ,B和C之间的球面距离为
,B和C之间的球面距离为![]() ,则过A、B、C三点的截面与球心的距离是
( )
,则过A、B、C三点的截面与球心的距离是
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.用简单随机抽样的方法从含有10个个体的总体中,抽取一个容量为2的样本,个体a 第一次未被抽到的概率是 ( )
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D)
![]()
5、以正方体的顶点为顶点,能作出的三棱锥的个数是 ( )
![]() B、
B、![]() C、
C、![]() -6 D、
-6 D、
![]()
6、一条长为60的线段夹在互相垂直的两个平面之间,它和这两个平面所成的角分别为45°和30°,这条线段的两个端点向平面的交线引垂线,则垂足间的距离是 ( )
A.30 B.20 C.15 D.12
7、已知:![]()
![]() ,
,
则![]() 等于
( )
等于
( )
A、n
B、![]() C、
C、![]() D、
D、![]()
8.电话号码由7个数字组成,每个数字可以是0,1,2,…,9中的任意一个数字,则电话号是由完全不相同的数字组成的概率为 ( )
(A) ![]() (B)
(B) ![]() (C)
(C)![]() (D)
(D)![]()
9.空间三条射线PA,PB,PC满足∠APC=∠APB=60°,∠BPC=90°,则二面角B-PA-C 的度数( )
A.等于90° B.是小于120°的钝角
C.是大于等于120°小于等于135°的钝角 D.是大于135°小于等于150°的钝角
10.直三棱柱ABC—A1B1C1的体积为V,点P、Q分别在侧棱AA1和CC1上如图, AP=C1Q,则四棱锥B—APQC的体积为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11、设正四棱锥S—ABCD的侧棱长为![]() ,底面边长为
,底面边长为![]() ,E是SA的中点,则异面直线BE与SC所成的角是
( )
,E是SA的中点,则异面直线BE与SC所成的角是
( )
A.30° B.45° C.60° D.90°
12、用二项式定理计算9.985,精确到1的近似值为 ( )
A、99000 B、99002 C、99004 D、99005
二、填空题:
13.函数y=x4—2x2+ 5在x[—2,2]上的最大值为____,最小值为____·
14.在△ABC中,BC=21,∠BAC=120°,△ABC所在平面外一点P到A、B、C的距离都是14,则P到平面ABC的距离为 .
15、设a>0,a≠1从a,a![]() 六个数中任取两个不同的数组成对数的底和真数,得到不同对数值的个数是______。
六个数中任取两个不同的数组成对数的底和真数,得到不同对数值的个数是______。
16、某班50名学生,现在采用随机抽样方法逐一从中抽取5名同学参加夏令营,学生甲最后一个去抽,则他被拍中的概率为______
三、解答题:
17、一个口袋内装有4个不同的红球,6个不同的白球,若取出一个红球记2分,取出一个白球记1分,从口袋中取5个球,使总分不小于7分的取法有多少种?
18.A是△BCD所在平面外的点,∠BAC=∠CAD=∠DAB=60°,AB=3,AC=AD=2.
(Ⅰ)求证:AB⊥CD;
(Ⅱ)求AB与平面BCD所成角的余弦值.
19.若![]() 的展开式中各奇数项二项式系数之和为32,中间项为2 500,求
的展开式中各奇数项二项式系数之和为32,中间项为2 500,求![]() 。
。
20、某公交候车室里一乘客乘坐汽车或电车都能回家,若在5分钟内电车到站的概率为![]() ,汽车到站的概率为
,汽车到站的概率为![]() ,计算该乘客在5分钟内,能坐上任何一种车回家的概率.
,计算该乘客在5分钟内,能坐上任何一种车回家的概率.
21.已知两曲线y=x2—1与y=1—x3,若两曲线在横坐标为xo的点处的切线互相平行,求两条切线方程。
22.如图,在三棱柱ABC—A1B1C1中,AB=![]() a,BC=CA=AA1=a,A1在底面ABC上的射影O在AC上.
a,BC=CA=AA1=a,A1在底面ABC上的射影O在AC上.
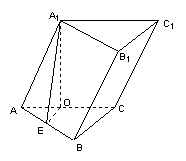 (Ⅰ)求AB与侧面AC1所成的角;
(Ⅰ)求AB与侧面AC1所成的角;
(Ⅱ)若O恰是AC的中点,求此三棱柱的侧面积.
高二数学综合训练一(第二学期)答案
一、BCABD AAABB CC
二、13、13 ;14、 7 ;15、 30 ;16、 0.1;
17、解:设取![]() 个红球,
个红球,![]() 个白球,于是:
个白球,于是:
![]() ,其中
,其中![]() ,
, ![]()
因此所求的取法种数是:![]() =186(种)
=186(种)
18.解(Ⅰ)∵∠BAC=∠CAD=∠DAB=60°, AC=AD=2,AB=3, ∴△ABC≌△ABD,BC=BD.
取CD的中点M,连AM、BM,则CD⊥AM,CD⊥BM. ∴CD⊥平面ABM,于是AB⊥BD.
(Ⅱ)由CD⊥平面ABM,则平面ABM⊥平面BCD,这样∠ABM是AB与平面BCD所成的角.
在△ABC中,AB=3,AC=2,∠BAC=60°,![]() . 在△ACD中, AC=AD=2,∠CAD=60°,∴△ACD是正三角形,AM=
. 在△ACD中, AC=AD=2,∠CAD=60°,∴△ACD是正三角形,AM=![]() . 在Rt△BCM中,BC=
. 在Rt△BCM中,BC=![]() ,CM=1,
,CM=1,
![]() .
.![]()
19.
解:x=25或![]()
提示:2n-1=32,中间项![]() =2500,
=2500,
即![]()
![]() log5x(log5x-1)=1
log5x(log5x-1)=1
20、 ![]()
21.12x+9y+13=0 ,36x+27y-11=0
22.如图,在三棱柱ABC—A1B1C1中,AB=![]() a,BC=CA=AA1=a,A1在底面ABC上的
a,BC=CA=AA1=a,A1在底面ABC上的
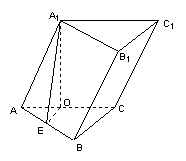 射影O在AC上.
射影O在AC上.
(Ⅰ)求AB与侧面AC1所成的角;
(Ⅱ)若O恰是AC的中点,求此三棱柱的侧面积.
解(Ⅰ)在△ABC中,AB=![]() ,BC=AC=a,∴△ABC是等腰直角三角形,BC⊥AC,∠CAB=45°,
,BC=AC=a,∴△ABC是等腰直角三角形,BC⊥AC,∠CAB=45°,
又BC⊥A1O,故BC⊥侧面AC1,AB与侧面AC1所成角就是
∠BAC=45°.
(Ⅱ)由(Ⅰ)知四边形B1BCC1为矩形,![]() 中点,
中点,
![]() 于E,连结A1E,则AB⊥A1E. 在Rt△AOE
于E,连结A1E,则AB⊥A1E. 在Rt△AOE
中,![]() ,在Rt△A1EO中,
,在Rt△A1EO中,![]()
![]() .
.
