|
2004-2005学年度上学期
高中学生学科素质训练
高二数学同步测试(1)—不等式的性质
一、选择题(本大题共10小题,每小题5分,共50分)
1.若![]() ,且
,且![]() ,则下列不等式中一定成立的是
( )
,则下列不等式中一定成立的是
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.对于任意实数a、b、c、d,命题: ( )
①![]() ;
;
②![]() ;
;
③![]() ;
;
④![]() ;
;
⑤![]() .
.
其中真命题的个数是 ( )
A.1 B.2 C.3 D.4
3.设 ![]() 成立的一个充要条件是 ( )
成立的一个充要条件是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.已知![]() 的取值范围是
( )
的取值范围是
( )
A.![]() B.
B.![]() C.
C.![]() D
.
D
.![]()
5.已知![]() ,且
,且![]() ,则
,则![]() 的最小值是
( )
的最小值是
( )
A. 32 B.![]() C.
C.![]() D.10
D.10
6.下列命题中,其正确的命题个数为 ( ) ①![]() 的最小值是2 ;②
的最小值是2 ;②![]() 的最小值是2;③
的最小值是2;③![]() 的最小值是2;
的最小值是2;
④![]() 的最小值是2;⑤
的最小值是2;⑤![]() 的最小值是2,
的最小值是2,
A.1 B.2 C.3 D.4
7.若a,b∈R+,下列不等式中正确的是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
8.已知![]() 是正数,且
是正数,且![]() ,则
,则![]() 的最小值是
( )
的最小值是
( )
A.6 B.12 C.16 D.24
9.设x>0,y>0,xy= 4,则![]() 取最小值时x的值为
( )
取最小值时x的值为
( )
A.1 B.2 C.![]() D.
D.![]()
10.甲、乙两人同时从A地出发B地,甲在前一半路程用速度![]() ,在后一半路程用速度
,在后一半路程用速度![]() ,乙在前一半时间用速度
,乙在前一半时间用速度![]() ,在后一半时间用速度
,在后一半时间用速度![]() ,则两人中谁先到达
,则两人中谁先到达
( )
A.甲 B.乙 C.两人同时 D.无法确定
二、填空题(本大题共4小题,每小题6分,共24分)
11.若![]() ,
,![]() ,则2a-b的取值范围是
.
,则2a-b的取值范围是
.
12.若x![]() R,则x2与x-1的大小关系是
.
R,则x2与x-1的大小关系是
.
13.函数![]() 的最小值是_____________,这时x的值为____________.
的最小值是_____________,这时x的值为____________.
14.已知![]() 时,函数有最_______值是 .
时,函数有最_______值是 .
三、解答题(本大题共6题,共76分)
15.已知![]() ,
,![]() ,
,![]() ,
,![]() ,试比较A、B、C的大小.(12分)
,试比较A、B、C的大小.(12分)
16.已知正数x、y满足![]() 的最小值.
的最小值.
![]()
![]()
![]() 判断以上解法是否正确?说明理由;若不正确,请给出正确解法.
判断以上解法是否正确?说明理由;若不正确,请给出正确解法.
(12分)
17.已知![]() (12分)
(12分)
18.已知![]() .求证:
.求证:
(1)![]() ;
;
(2)![]() .(12分)
.(12分)
19.某工厂用7万元钱购买了一台新机器,运输安装费用2千元,每年投保、动力消耗的费用也为2千元,每年的保养、维修、更换易损零件的费用逐年增加,第一年为2千元,第二年为3千元,第三年为4千元,依此类推,即每年增加1千元.问这台机器最佳使用年限是多少年?并求出年平均费用的最小值.(14分)
20.已知函数![]() 在R上是增函数,
在R上是增函数,![]() .
.
(1)求证:如果![]() ;
;
(2)判断(1)中的命题的逆命题是否成立?并证明你的结论;
解不等式![]() .(14分)
.(14分)
参考答案
一、选择题(本大题共10小题,每小题5分,共50分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | D | B | A | C | B | D | C | C | B | B |
二、填空题(本大题共4小题,每小题6分,共24分)
11.![]() 12.
12.![]() 13.
13.![]() 14.
14.![]()
三、解答题(本大题共6题,共76分)
15.(12分)
[解析]:不妨设![]() ,则
,则![]() ,
,![]() ,
,![]() 由此猜想
由此猜想![]()
由![]() 得
得![]() ,
,![]() 得
得![]() ,
,
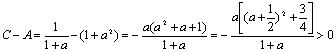 得
得![]() ,即得
,即得![]() .
.
16.(12分)
[解析]:错误. ![]() 等号当且仅当x=y时成立,又
等号当且仅当x=y时成立,又![]() 等号当且仅当x=2y时成立,而①②的等号同时成立是不可能的.
等号当且仅当x=2y时成立,而①②的等号同时成立是不可能的.
正确解法:因为x >0,y>0,且x +2y=1,
![]() ,当且仅当
,当且仅当
![]() ∴这时
∴这时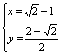 .
.
17.(12分)
[解析] ![]() ,
,
∴(1)当a>1时,a-1>0 ∴![]() 上递增,∴
上递增,∴![]()
(2)当0<a<1时,a-1<0 ∴![]() 上递减,∴
上递减,∴![]()
综上(1)(2)知:x>y.
18.(12分)
[证明]:(1)![]() ,
,![]() ,
,![]() ,
,
![]()
![]()
![]()
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]()
(2)[解法1]由(1)知![]()
又![]()
![]()
![]() .
.
[解法2]:首先易证![]()
![]()
![]()
![]()
![]()
![]()
19.(14分)
[解析]设这台机器最佳使用年限是n年,则n年的保养、维修、更换易损零件的总费用为:
![]() ,
,
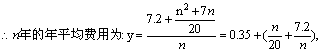
![]()
等号当且仅当![]()
![]()
答:这台机器最佳使用年限是12年,年平均费用的最小值为1.55万元.
20.(14分)
(1)证明:当![]()
![]()
(2)中命题的逆命题为:![]() ①
①
①的逆否命题是:![]() ②
②
仿(1)的证明可证②成立,又①与②互为逆否命题,故①成立,即(1)中命题的逆命题成立. 根据(2),所解不等式等价于![]() .
.
