高二数学（理）第二学期期末联考模拟试题

一、填空题：本大题共14小题,每小题5分，共计70分．不需写出解答过程,请把答案直接填写在答题卡相应位置上.

1．复数的值是　_▲_　

2．在中，则外接圆的半径，运用类比方法，三棱锥的三条侧棱两两垂直且长度分别为则其外接球的半径为等于　_▲_　　

3．等于　_▲_　　

4．某城市的汽车牌照号码由2个英文字母后接4个数字组成，其中4个数字互不相同的牌照号码共有　_▲_　　

5.已知,则( 的值等于　_▲_　　

6. 设随机变量~，且，则_▲_　　

7.　 10张奖券中只有3张有奖，5个人购买，每人1张，至少有1人中奖的概率是　_▲_　　

8. 将三颗骰子各掷一次，设事件A=“三个点数都不相同”，B=“至少出现一个3点”，则概率等于　_▲_　　

9．若的二项展开式中的系数为，则　_▲_　　（用数字作答）．

10．复数，且，若是实数，则有序实数对可以是　_▲_　　　　．（写出一个有序实数对即可）

11．将5本不同的书全发给4名同学，

每名同学至少有一本书的概率是　　 _▲_　　　　；　　　　　　　　　　　　　　

12．如右图，用6种不同的颜色给图中的4个格子涂色，

每个格子涂一种颜色，要求最多使用3种颜色且相邻的两个格子颜色不同，则不同的涂色方法共有　_▲_　　　种（用数字作答）．

13．将杨辉三角中的奇数换成1，偶数换成0，得到如图1所示的0—1三角数表．从上往下数，第1次全行的数都为1的是第1行，第2次全行的数都为1的是第3行，…，第次全行的数都为1的是第　_▲_　　  行；

第1行　　　　　 1　　1

第2行　　　　 1　 0　 1

第3行　　　 1　 1　 1　 1

第4行　　 1　 0　 0　 0　 1

第5行　 1　 1　 0　 0　 1　 1

……　 ………………………………………

14、若直线 x + y = m 与圆 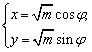 (φ为参数，m>0)相切，则m为　 ▲　 ．

二、解答题：本大题共6小题，共计90分．请在答题卡指定区域内作答，解答时应写出字说明、证明过程或演算步骤．

15、从5名女同学和4名男同学中选出4人参加演讲比赛，分别按下列要求，各有多少种不同选法？

⑴男、女同学各2名；　　

⑵男、女同学分别至少有1名；

⑶在(2)的前提下，男同学甲与女同学乙不能同时选出.

16．（1）已知,求的值；

（2）设复数满足,且是纯虚数,求.

17．某研究机构为了研究人的脚的大小与身高之间的关系,随机抽测了20人,得到如下数据:

序　　　号	1	2	3	4	5	6	7	8	9	10
身高x(厘米)	192	164	172	177	176	159	171	166	182	166
脚长y( 码 )	48	38	40	43	44	37	40	39	46	39
序　　　号	11	12	13	14	15	16	17	18	19	20
身高x(厘米)	169	178	167	174	168	179	165	170	162	170
脚长y( 码 )	43	41	40	43	40	44	38	42	39	41

(1)若“身高大于175厘米”的为“高个”，“身高小于等于175厘米”的为“非高个”；“脚长大于42码”的为“大脚”，“脚长小于等于42码”的为“非大脚”.请根据上表数据完成下面的联列表:

	高　个	非高个	合　计
大　脚
非大脚		12
合　计			20

(2)根据题(1)中表格的数据,若按99%的可靠性要求,能否认为脚的大小与身高之间有关系?

(3)若按下面的方法从这20人中抽取1人来核查测量数据的误差:将一个标有数字1,2,3,4,5,6的正六面体骰子连续投掷两次,记朝上的两个数字的乘积为被抽取人的序号.试求:①抽到12号的概率；②抽到“无效序号(超过20号)”的概率.

18．某地区为下岗人员免费提供财会和计算机培训，以提高下岗人员的再就业能力，每名下岗人员可以选择参加一项培训、参加两项培训或不参加培训，已知参加过财会培训的有60%，参加过计算机培训的有75%，假设每个人对培训项目的选择是相互独立的，且各人的选择相互之间没有影响．（用数字作答）

（I）任选1名下岗人员，求该人参加过培训的概率；

（II）任选3名下岗人员，记为3人中参加过培训的人数，求的分布列和数学期望．

19．（1）在的展开式中，若第项与第项系数相等，则等于多少？

（2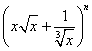）的展开式奇数项的二项式系数之和为，则求展开式中二项式系数最大的项　

（3）已知展开式中的二项式系数的和比展开式的二项式系数的和大,求展开式中的系数最大的项和系数最小的项　

20．已知为正整数，

（I）用数学归纳法证明：当时，；

（II）对于，已知

求证：；

（III）求出满足等式的所有正整数．

参考答案

1、0　　2、　 3、  　 4、　　5、　　6、　

 7、　　 8、　　　9、2　 10、（或满足的任一组非零实数对）  11、　12、390　　 13、　　　　　 14、2

15、[解]：⑴＝60 …4分

　⑵＝120…8分

⑶120-()＝99 …12分

16．（1）……4分

（2）解：设，由得；……6分

是纯虚数，则……8分

， ……12分

……14分

17、 解: (Ⅰ)表格为:

	高　个	非高个	合　计
大　脚	5	2	7
非大脚	1		13
合　计	6	14

 (说明:黑框内的三个数据每个1分,黑框外合计数据有错误的暂不扣分)

(Ⅱ)提出假设H₀: 人的脚的大小与身高之间没有关系. ……………………………………………

　 根据上述列联表可以求得.……………………………………　 当H₀成立时,的概率约为0.005,而这里8.802>7.879,

所以我们有99.5%的把握认为: 人的脚的大小与身高之间有关系. ………………………………

　 (Ⅲ) ①抽到12号的概率为……………………………………………………………

②抽到“无效序号(超过20号)”的概率为

18．解：任选1名下岗人员，记“该人参加过财会培训”为事件，“该人参加过计算机培训”为事件，由题设知，事件与相互独立，且，．

（I）解法一：任选1名下岗人员，该人没有参加过培训的概率是

所以该人参加过培训的概率是．……5分

解法二：任选1名下岗人员，该人只参加过一项培训的概率是

该人参加过两项培训的概率是．

所以该人参加过培训的概率是．……5分

（II）因为每个人的选择是相互独立的，所以3人中参加过培训的人数服从二项分布，，，即的分布列是：……13分

（每格2分，共8分！）

	0	1	2	3
	0.001	0.027	0. 243	0.729

的期望是．……15分

（或的期望是）

19．解：（1）由已知得……3分

（2）由已知得，……5分

而展开式中二项式系数最大项是　……7分

（3）　解：，……9分

的通项

当时，展开式中的系数最大，即为展开式中的系数最大的项；……11分

当时，展开式中的系数最小，即为展开式中的系数最小的项　……15分

20．解法1：（Ⅰ）证：用数学归纳法证明：

（ⅰ）当时，原不等式成立；当时，左边，右边，

因为，所以左边右边，原不等式成立；……2分

（ⅱ）假设当时，不等式成立，即，则当时，

，，于是在不等式两边同乘以得

，

所以．即当时，不等式也成立．

综合（ⅰ）（ⅱ）知，对一切正整数，不等式都成立．……5分

（Ⅱ）证：当时，由（Ⅰ）得：，

（令易知）……7分

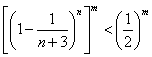于是，．……10分

（Ⅲ）解：由（Ⅱ）知，当时，

，

．……12分

即．即当时，不存在满足该等式的正整数．

故只需要讨论的情形：

当时，，等式不成立；

当时，，等式成立；

当时，，等式成立；

当时，为偶数，而为奇数，故，等式不成立；

当时，同的情形可分析出，等式不成立．　　综上，所求的只有．……15分