宣威六中高二数学月考试卷

命题　惠德志

一、　　　　　 选择题（每小题5分，共60分）

1. 若直线x = 1的倾斜角为α ，则α（　　）

A.　等于0　　　　　　　　　　 B. 等于　

C.　等于　　　　　　　　　　 D. 不存在

2、直线和的夹角是（　）

　　　　 A．　　　　　　　　　 B. 　　　　　　　　　　

C. 　　　　　　　　　　 D.

3、三点A (3, 1),B (－2, k), C (8, 11)在同一直线上，则k的值是（　　）

A.－6　　　　 B.－7　　　C.－8　　 D.－9

4、直线x+y+2=0过点（－1，1），且与直线垂直，那么（　）

A. =1, =0 　　　　　　　　　 B. =0, =1 　

　 C. , 　　　　　　　 D. ,

5、A点关于8x+6y=25的对称点恰为原点，则A点的坐标为（　）

　 A.(2, )　　　B.　　　 C.(3, 4)　　　　　D.(4, 3)

6. 已知直线l的倾斜角满足，则l的斜率为（　）

　　A. 　　　　 B. 　　　C. 或　　　D. 或

7. 已知直线，下列说法正确的是（　）

　　A. 到的角是　　　　　B. 到的角是

　　C. 到的角是　　　　　D. 与的夹角是

8、直线的斜率，则此直线的倾斜角的取值范围是（　）

　 A．　　　　　　　　　 B. 　　

C. ,　　　　　　　　 D.

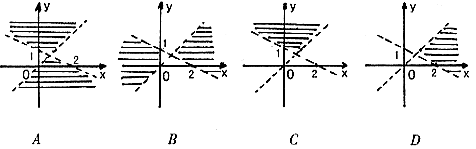
9. 满足不等式的点（x，y）所在的区域应为（　）

10.已知方程和表示两条直线平行，则a的值为（　）

　　　A．1或　　　　　　　　　 B.0　　　　　　　　　　　

　C. 　　　　　　　　　　 D.0或

11. 已知l₁与l₂两条直线关于直线y=x对称, l₁: , l₂: y=kx+b那么k与b的积等于(　　 )

　　 A. 15　　　　　B. 30　　　　　　C. 45　　　　　　D. 60

12.曲线f(x,y)=0关于直线x-y-2=0的对称曲线的方程为(　 )

A.f(y+2,x)=0　　　　　　　　　　　　　　B.f(x-2,y)=0

C.f(y+2,x-2)=0　　　　　　　　　　　　　D.f(y-2,x+2)=0

二、填空

10.直线关于点（1，0）对称的直线方程是

14. 不等式组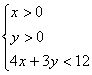　表示的平面区域内的整点（横坐标和纵坐标都是整数的点）

共有　　　　　　　　　个.

　 O　　　2　　4　 x

15. 如图所示直线L,对于直线上的点（x,y）,当x的

值从0变到5时，则y的值从2变到_____

16. 一条直线l过定点P(1,2), 且与

点M(4,-8)和点Q(2,0)距离相等,

则l的方程是___________

高二年级数学月考答题卡

一、选择题（每小题5分，共60分，把正确答案的符号填在下列表格中）

题号	1	2	3	4	5	6	7	8	9	10	11	12	小计
答案

二、填空题（每小题4分,共16分. 把每小题的答案填在试卷对应题号的横线上）

13　　　　　　　　　　　　　　　 14

15　　　　　　　　　　　　　　　 16　　　　　

17.求倾斜角是45°,并且与原点的距离是5的直线的方程

18．已知过点P的直线l绕点P按逆时针方向旋转角﹝0＜＜﹞，得直线为　　　 x－y－2 = 0，若继续按逆时针方向旋转－角，得直线2x＋y－1 = 0，求直线l的方程.

19.P为直线l:2x+3y-6＝0上一动点，M(3,1)为一定点，点Q在直线MP上，且MQ：QP＝2，求Q点轨迹

20．试在直线l：x-y+1=0上找一点M,使点M到两点A(1,0)、B(3,0)的距离和最小，求出此时点M的坐标。

21.私人办学是教育发展的方向，某人准备投资1200万元兴办一所完全中学，为了考虑社会效益和经济效益，对该地区教育市场进行调查，得出一组数据列表(以班级为单位)：

市场调查表

班级学生数

配备教师数

硬件建设

(万元)

教师年薪

(万元)

初中

2.0

1.2

高中

2.5

1.6

根据物价部门的有关文件，初中是义务教育阶段，收费标准适当控制，预计除书本费、办公费以外每生每年可收取600元，高中每生每年可收取1500元.因生源和环境等条件限制，办学规模以20至30个班为宜,请你合理地安排招生计划，使年利润最大.

22、已知ABC的三个顶点A(4,1)、B(7,5)、C(-4,7)，

（1）　求BC边上的中线所在直线的方程；

（2）　求BC边上高线所在直线的方程；

（3）求∠A的内角平分线所在直线的方程。

高二年级数学月考答题卡

一、选择题（每小题5分，共60分，把正确答案的符号填在下列表格中）

题号	1	2	3	4	5	6	7	8	9	10	11	12	小计
答案	D	C	D	B	D	D	C	D	B	D	D	C

二、填空题（每小题4分,共16分. 把每小题的答案填在试卷对应题号的横线上）

13、 2x-3y-5=0　　　　　　　　　　　　 14、3

15、　　　　　　　　　　　　　　　 16、3x+y-5=0或4x+y-6=0

三、解答题（本部分共6道题，满分为74分）

17、解：因直线斜率为tan45⁰=1，可设直线方程y=x+b，　　　　　　　　 3分

　　　　化为一般式x-y+b=0　　　　　　　　　　　　　　　　　　　　　 5分

　　　　由直线与原点距离是5，得　　　　　　　　　　　　　　　　　　

　　　　　　　　　　　　　　　　　　　　　 8分

　　　　　　　　　　　　　　　　　　10分

所以直线方程为x-y+5=0,或x-y-5=0　　　　　　　　　　12分

18、由得 P ( 1,－1)

　据题意，直线l与直线垂直，故l斜率

　 ∴ 直线l方程为　即

19、答案6x+9y-21=0

20、作A（1，0）关于直线L的对称点A’，过A’、B的直线与L交于M，

A’

　　　　 A　　 B　x

则点M为所求的点。　　　　　　　　　　　　　　　　　　　　　2分

设A’(m,n)，因为AA’关于L对称

所以AA’垂直于L，

且AA’中点在L上，故

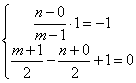得A’（-1，2）。　　　　　　　　　　　　 6分

所以A’B的方程x+2y-3=0　　　　　　　　　　　　　　　　　　 9分

解得M（）　　　　　　　　　　　　　　　12分

21、解：设初中编制为x个班，高中编制为y个班，则

20≤x+y≤30,　　　　　　　　　　　　　　　①

28x+58y≤1200.　　　　　　　　　　　　　　②

(x>0,y>0,x,y∈Z)记年利润为S，那么S＝3x+6y-2.4x-4y，即

S＝0.6x+2y.

如下图所示，作出①，②表示的平面区域，问题转化为在图中阴影部分求直线0.6x+2y-S＝0截距的最大值，过点A作0.6x+2y＝0的平行线即可求出S的最大值.

联立A的坐标为(18，12).

将x＝18,y＝12代入③，得S_max＝34.8.

22．（1）设BC边上的中线为AD

　　　　因为B（7，5） C（-4，7）

中点D（3/2，6），　且A（4，1）

　　　　所以中线AD所在直线方程：2x+y-9=0　　　　　　　　　　　　　 4分

(2)设BC边上的高线为AE

　因为BC边斜率为k_BC=-2/11,所以高线AE斜率为11/2，

　又A（4，1），由点斜式可得AE方程：

　 11x-2y-42=0　　　　　　　　　　　　　　　　　　　　　　　　 8分

(3)设A的平分线为AF，其斜率为k

易知k_ABk_AC=-1,所以∠BAC=90⁰,　　　　　　　　　　　　　　　　　　 10分

从而∠BAF=45⁰，即AB到AF的角为45⁰，由到角公式得

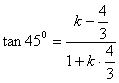，解得k=-7

所以AF的方程y-1=-7(x-4)即7x+y-27=0　　　　　　　　　　　　　　14分

宣威六中高二数学月考试卷

A. 15 B. 30 C. 45 D. 60

　　 A. 15　　　　　B. 30　　　　　　C. 45　　　　　　D. 60