2004-2005学年度上学期
高中学生学科素质训练
高二数学同步测试(6)—线性规划
一、选择题(本大题共10小题,每小题5分,共50分)
1.不在 3x+ 2y < 6 表示的平面区域内的一个点是 ( )
A.(0,0) B.(1,1) C.(0,2) D.(2,0)
2.已知点(3 , 1)和点(-4 , 6)在直线 3x–2y + m = 0 的两侧,则 ( )
A.m<-7或m>24 B.-7<m<24
C.m=-7或m=24 D.-7≤m≤ 24
3.若![]() ,则目标函数 z = x + 2 y 的取值范围是
( )
,则目标函数 z = x + 2 y 的取值范围是
( )
A.[2 ,6] B. [2,5] C. [3,6] D. [3,5]
4.不等式![]() 表示的平面区域是一个 ( )
表示的平面区域是一个 ( )
A.三角形 B.直角三角形 C.梯形 D.矩形
5.在△ABC中,三顶点坐标为A(2 ,4),B(-1,2),C(1 ,0 ), 点P(x,y)在△ABC内部及边界运动,则 z= x – y 的最大值和最小值分别是 ( )
A.3,1 B.-1,-3 C.1,-3 D.3,-1
6.在直角坐标系中,满足不等式 x2-y2≥0 的点(x,y)的集合(用阴影部分来表示)的
是 ( )
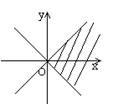
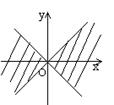
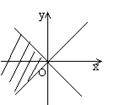
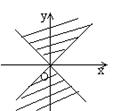
A B C D
7.不等式![]() 表示的平面区域内的整点个数为 ( )
表示的平面区域内的整点个数为 ( )
A. 13个 B. 10个 C. 14个 D. 17个
8.不等式![]() 表示的平面区域包含点
表示的平面区域包含点![]() 和点
和点![]() 则
则![]() 的取值范围是
的取值范围是
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
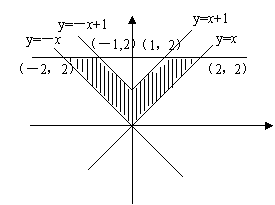
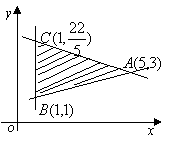 9.已知平面区域如右图所示,
9.已知平面区域如右图所示,![]() 在平面区域内取得最大值的最优解有无数多个,则
在平面区域内取得最大值的最优解有无数多个,则![]() 的值为
( )
的值为
( )
A.![]() B.
B.![]()
C.![]() D.不存在
D.不存在
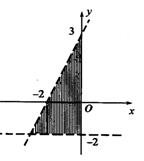 10.如图所示,表示阴影部分的二元一次不等式组是 ( )
10.如图所示,表示阴影部分的二元一次不等式组是 ( )
A.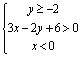 B.
B.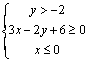
C.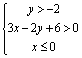 D.
D.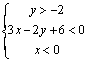
二、填空题(本题共4小题,每小题6分,共24分)
![]() 11.已知x,y满足约束条件
11.已知x,y满足约束条件 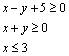 ,则
,则![]() 的最小值为______________.
的最小值为______________.
12.已知约束条件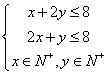 ,目标函数z=3x+y,某学生求得x=
,目标函数z=3x+y,某学生求得x=![]() , y=
, y=![]() 时,zmax=
时,zmax=![]() , 这显然不合要求,正确答案应为x=
; y=
; zmax=
.
, 这显然不合要求,正确答案应为x=
; y=
; zmax=
.
13.某电脑用户计划用不超过500元的资金购买单价分别为60元,70元的单片软件和盒装磁盘,根据需要软件至少买3件,磁盘至少买2盒,则不同的选购方式共有______________种.
14.已知x,y满足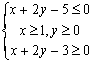 ,则
,则![]() 的最大值为___________,最小值为____________. 三、解答题(本大题共6题,共76分)
的最大值为___________,最小值为____________. 三、解答题(本大题共6题,共76分)
15.由![]() 围成的几何图形的面积是多少?(12分)
围成的几何图形的面积是多少?(12分)
16.已知![]() 当a为何值时,直线
当a为何值时,直线![]() 及坐标轴围成的平面区域的面积最小?(12分)
及坐标轴围成的平面区域的面积最小?(12分)
| 方式种类 | 轮船 | 飞机 |
| 小麦 | 300吨 | 150吨 |
| 大米 | 250吨 | 100吨 |
17.有两种农作物(大米和小麦),可用轮船和飞机两种方式运输,每天每艘轮船和每架飞机运输效果如下:在一天内如何安排才能合理完成运输2000吨小麦和1500吨大米的任务?(12分)
18.设![]() ,式中变量
,式中变量![]() 满足条件
满足条件 ,求z的最小值和最大值.(12分)
,求z的最小值和最大值.(12分)
19.某家俱公司生产甲、乙两种型号的组合柜,每种柜的制造白坯时间、油漆时间及有关数据如下:
| 工艺要求 | 产品甲 | 产品乙 | 生产能力/(台/天) |
| 制白坯时间/天 | 6 | 12 | 120 |
| 油漆时间/天 | 8 | 4 | 64 |
| 单位利润/元 | 20 | 24 |
|
问该公司如何安排甲、乙二种柜的日产量可获最大利润,并且最大利润是多少?(14分)
20.某运输公司接受了向抗洪抢险地区每天至少送180t支援物资的任务.该公司有8辆载重为6t的A型卡车与4辆载重为10t的B型卡车,有10名驾驶员;每辆卡车每天往返的次数为A型卡车4次,B型卡车3次;每辆卡车每天往返的成本费A型车为320元,B型车为504元.请你们为该公司安排一下应该如何调配车辆,才能使公司所花的成本费最低?若只调配A型或B型卡车,所花的成本费分别是多少?(14分)
参考答案
一.选择题(本大题共10小题,每小题5分,共50分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | D | B | A | C | C | B | A | A | A | C |
二.填空题(本大题共4小题,每小题6分,共24分)
11. ![]() 12.3,2,11 13. 7 14. 2,0
12.3,2,11 13. 7 14. 2,0
三、解答题(本大题共6题,共76分)
 15.(12分)[解析]:如下图由
15.(12分)[解析]:如下图由![]() 围成的几何图形就是其阴影部分,且
围成的几何图形就是其阴影部分,且![]() .
.
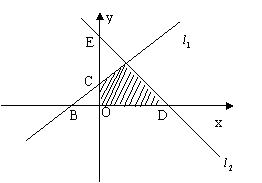
16.(12分)[解析]: 如图![]()
![]()
![]()
![]() ,
,
![]() ,由题意知
,由题意知![]() 及坐标轴围成的平面区域为ACOD,
及坐标轴围成的平面区域为ACOD,
![]()
![]() .
.
17.(12分)[解析]:设轮船为x艘、飞机为y架,则可得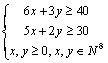 ,目标函数z=x+y,作出可行域,利用图解法可得点A(
,目标函数z=x+y,作出可行域,利用图解法可得点A(![]() ,0)可使目标函数z=x+y最小,但它不是整点,调整为B(7,0).
,0)可使目标函数z=x+y最小,但它不是整点,调整为B(7,0).
答:在一天内可派轮船7艘,不派飞机能完成运输任务.
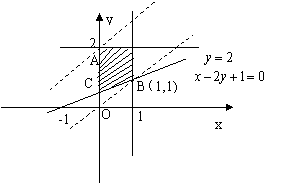 18.(12分)
18.(12分)
[解析]: 作出满足不等式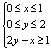 的可行域,如右图所示.
的可行域,如右图所示.
作直线![]()
![]()
![]()
19.(14分)

![]() [解析]:设x,y分别为甲、乙二种柜的日产量,可将此题归纳为求如下线性目标函数Z=20x+24y的最大值.其中线性约束条件为
[解析]:设x,y分别为甲、乙二种柜的日产量,可将此题归纳为求如下线性目标函数Z=20x+24y的最大值.其中线性约束条件为 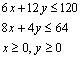 ,由图及下表
,由图及下表
| (x,y) | Z=20x+24y |
| (0,10) | 240 |
| (0,0) | 0 |
| (8,0) | 160 |
| (4,8) | 272 |
Zmax=272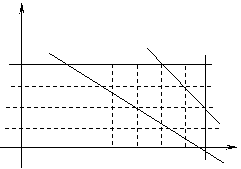 答:该公司安排甲、乙二种柜的日产量分别为4台和8台可获最大利润272元.
答:该公司安排甲、乙二种柜的日产量分别为4台和8台可获最大利润272元.
| A型车 | B型车 | 物资限制 | |
| 载重(t) | 6 | 10 | 共180 |
| 车辆数 | 8 | 4 | |
| 出车次数 | 4 | 3 | |
| 每车每天运输成本(元) | 320 | 504 |
|
x+y=10
1 4 5 6 7 8 4x+5y=30 |
20.(14分)
解:设每天调出A型车x辆、B型车y辆,公
司所花的成本为z元,则
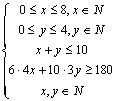 目标函数z=320x+504y,
目标函数z=320x+504y,
作出可行域(如上图),作L:320x+504y=0, 可行域内的点E点(7.5,0)可使Z最小,但不是整数点,最近的整点是(8,0)即只调配A型卡车,所花最低成本费z=320×8=2560(元);
若只调配B型卡车,则y无允许值,即无法调配车辆.