高二理科数学下学期期末试卷 (理科)
班级 学号 姓名 分数
第I卷(选择题共60分)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.复数![]() 等于( D
)
等于( D
)
A.![]() B.
B.![]() C.1 D.
C.1 D.![]()
2.函数![]() 的图像关于( C )
的图像关于( C )
A.![]() 轴对称 B. 直线
轴对称 B. 直线![]() 对称
对称
C. 坐标原点对称 D.
直线![]() 对称
对称
3.记等差数列![]() 的前
的前![]() 项和为
项和为![]() ,若
,若![]() ,
,![]() ,则
,则![]() ( D
)
( D
)
A.16 B.
4.已知![]() ,b都是实数,那么“
,b都是实数,那么“![]() ”是“
”是“![]() >b”的D
>b”的D
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
5.在△ABC中,角ABC的对边分别为a、b、c,若(a2+c2-b2)tanB=![]() ,则角B的值为D
,则角B的值为D
A. ![]() B.
B.
![]() C.
C.![]() 或
或![]() D.
D.
![]() 或
或![]()
6.设![]() 是球心
是球心![]() 的半径
的半径![]() 上的两点,且
上的两点,且![]() ,分别过
,分别过![]() 作垂直于
作垂直于![]() 的面截球得三个圆,则这三个圆的面积之比为:( D )
的面截球得三个圆,则这三个圆的面积之比为:( D )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
7.在![]() 中,
中,![]() ,
,![]() .若点
.若点![]() 满足
满足![]() ,则
,则![]() ( A
)
( A
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 若函数
若函数
9.若双曲线![]() 的两个焦点到一条准线的距离之比为3:2,则双曲线的离心率是D
的两个焦点到一条准线的距离之比为3:2,则双曲线的离心率是D
(A)3 (B)5
(C)![]() (D)
(D)![]()
8.![]() 的值域是
的值域是![]() ,则函数
,则函数![]() 的值域是B
的值域是B
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 10.已知函数
10.已知函数![]() ,
,![]() 是
是![]() 的反函数,若
的反函数,若![]() (
(![]() ),则
),则![]() 的值为( A
)
的值为( A
)
A.![]() B.1 C.4 D.10
B.1 C.4 D.10
11.设曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,则
垂直,则![]() ( D )
( D )
A.2 B.![]() C.
C.![]() D.
D.![]()
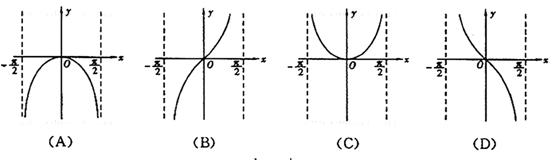
12.函数y=lncosx(-![]() <x<
<x<![]() 的图象是A
的图象是A
第Ⅱ卷(非选择题 共90分)
考生注意事项:
请用0.5毫米黑色墨水签字笔在答题卡上书写作答,在试题卷上书写作答无效.
二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡的相应位置.
13.在![]() 的展开式中,含
的展开式中,含![]() 的项的系数是
。-15
的项的系数是
。-15
14. ![]() .
. ![]()
15.已知随机变量![]() 服从正态分布N(3,a2),则P(
服从正态分布N(3,a2),则P(![]() =
。
=
。![]()
![]()
16.某地奥运火炬接力传递路线共分6段,传递活动分别由6名火炬手完成.如果第一棒火炬手只能从甲、乙、丙三人中产生,最后一棒火炬手只能从甲、乙两人中产生,则不同的传递方案共有 种.(用数字作答).96
三、解答题:本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.
17(本小题满分12分)
已知函数![]() (
(![]() )的最小值正周期是
)的最小值正周期是![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求函数![]() 的最大值,并且求使
的最大值,并且求使![]() 取得最大值的
取得最大值的![]() 的集合.
的集合.
(17)本小题主要考查特殊角三角函数值、两角和的正弦、二倍角的正弦与余弦、函数![]() 的性质等基础知识,考查基本运算能力.满分12分.
的性质等基础知识,考查基本运算能力.满分12分.
(Ⅰ)解:
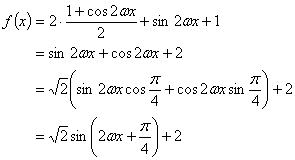
由题设,函数![]() 的最小正周期是
的最小正周期是![]() ,可得
,可得![]() ,所以
,所以![]() .
.
(Ⅱ)由(Ⅰ)知,![]() .
.
当![]() ,即
,即![]() 时,
时,![]() 取得最大值1,所以函数
取得最大值1,所以函数![]() 的最大值是
的最大值是![]() ,此时
,此时![]() 的集合为
的集合为![]() .
.
18.(本小题共13分)
甲、乙等五名奥运志愿者被随机地分到![]() 四个不同的岗位服务,每个岗位至少有一名志愿者.
四个不同的岗位服务,每个岗位至少有一名志愿者.
(Ⅰ)求甲、乙两人同时参加![]() 岗位服务的概率;
岗位服务的概率;
(Ⅱ)求甲、乙两人不在同一个岗位服务的概率;
(Ⅲ)设随机变量![]() 为这五名志愿者中参加
为这五名志愿者中参加![]() 岗位服务的人数,求
岗位服务的人数,求![]() 的分布列.
的分布列.
解:(Ⅰ)记甲、乙两人同时参加![]() 岗位服务为事件
岗位服务为事件![]() ,那么
,那么![]() ,
,
即甲、乙两人同时参加![]() 岗位服务的概率是
岗位服务的概率是![]() .
.
(Ⅱ)记甲、乙两人同时参加同一岗位服务为事件![]() ,那么
,那么![]() ,
,
所以,甲、乙两人不在同一岗位服务的概率是![]() .
.
(Ⅲ)随机变量![]() 可能取的值为1,2.事件“
可能取的值为1,2.事件“![]() ”是指有两人同时参加
”是指有两人同时参加![]() 岗位服务,
岗位服务,
则![]() .
.
所以![]() ,
,![]() 的分布列是
的分布列是
|
| 1 | 3 |
|
|
|
|
···································································································································· 12分
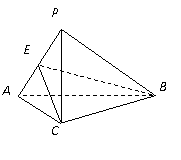
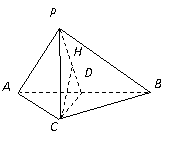
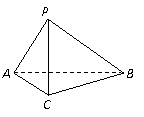 3.如图,在三棱锥
3.如图,在三棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求证:![]() ;
;
(Ⅱ)求二面角![]() 的大小;
的大小;
(Ⅲ)求点![]() 到平面
到平面![]() 的距离.
的距离.
解法一:
(Ⅰ)取![]() 中点
中点![]() ,连结
,连结![]() .
.
![]() ,
,
![]() .
.
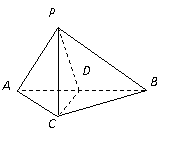
![]() ,
,
![]() .
.
![]() ,
,
![]() 平面
平面![]() .
.
![]() 平面
平面![]() ,
,
![]() .
.
(Ⅱ)![]() ,
,![]() ,
,
![]() .
.
又![]() ,
,
![]() .
.
又![]() ,即
,即![]() ,且
,且![]() ,
,
![]() 平面
平面![]() .
.
取![]() 中点
中点![]() .连结
.连结![]() .
.
![]() ,
,![]() .
.
![]() 是
是![]() 在平面
在平面![]() 内的射影,
内的射影,
![]() .
.
![]() 是二面角
是二面角![]() 的平面角.
的平面角.
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]() .
.
![]() 二面角
二面角![]() 的大小为
的大小为![]() .
.
(Ⅲ)由(Ⅰ)知![]() 平面
平面![]() ,
,
![]() 平面
平面![]() 平面
平面![]() .
.
过![]() 作
作![]() ,垂足为
,垂足为![]() .
.
![]() 平面
平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .
.
![]() 的长即为点
的长即为点![]() 到平面
到平面![]() 的距离.
的距离.
由(Ⅰ)知![]() ,又
,又![]() ,且
,且![]() ,
,
![]() 平面
平面![]() .
.
![]() 平面
平面![]() ,
,
![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,
![]() .
.
![]() .
.
![]() 点
点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
解法二:
(Ⅰ)![]() ,
,![]() ,
,
![]() .
.
又![]() ,
,
![]() .
.
![]() ,
,
![]() 平面
平面![]() .
.
![]() 平面
平面![]() ,
,
![]() .
.
(Ⅱ)如图,以![]() 为原点建立空间直角坐标系
为原点建立空间直角坐标系![]() .
.
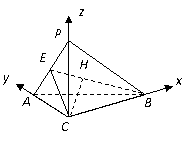 则
则![]() .
.
设![]() .
.
![]() ,
,
![]() ,
,![]() .
.
取![]() 中点
中点![]() ,连结
,连结![]() .
.
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
![]() 是二面角
是二面角![]() 的平面角.
的平面角.
![]() ,
,![]() ,
,![]() ,
,
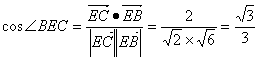 .
.
![]() 二面角
二面角![]() 的大小为
的大小为![]() .
.
(Ⅲ)![]() ,
,
![]() 在平面
在平面![]() 内的射影为正
内的射影为正![]() 的中心
的中心![]() ,且
,且![]() 的长为点
的长为点![]() 到平面
到平面![]() 的距离.
的距离.
如(Ⅱ)建立空间直角坐标系![]() .
.
![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() .
.
![]() .
.
![]() 点
点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
20.(本小题满分12分)
在数列![]() 中,
中,![]() ,
,![]() ,且
,且![]() (
(![]() ).
).
(Ⅰ)设![]() (
(![]() ),证明
),证明![]() 是等比数列;
是等比数列;
(Ⅱ)求数列![]() 的通项公式;
的通项公式;
本小题主要考查等差数列、等比数列的概念、等比数列的通项公式及前![]() 项和公式,考查运算能力和推理论证能力及分类讨论的思想方法.满分12分.
项和公式,考查运算能力和推理论证能力及分类讨论的思想方法.满分12分.
(Ⅰ)证明:由题设![]() (
(![]() ),得
),得
![]() ,即
,即![]() ,
,![]() .
.
又![]() ,
,![]() ,所以
,所以![]() 是首项为1,公比为
是首项为1,公比为![]() 的等比数列.
的等比数列.
(Ⅱ)解法:由(Ⅰ)
![]() ,
,
![]() ,
,
……
![]() ,(
,(![]() ).
).
将以上各式相加,得![]() (
(![]() ).
).
所以当![]() 时,
时,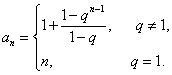
上式对![]() 显然成立.
显然成立.
21.在直角坐标系![]() 中,点P到两点
中,点P到两点![]() ,
,![]() 的距离之和等于4,设点P的轨迹为
的距离之和等于4,设点P的轨迹为![]() ,直线
,直线![]() 与C交于A,B两点.
与C交于A,B两点.
(Ⅰ)写出C的方程;
(Ⅱ)若![]()
![]()
![]() ,求k的值;
,求k的值;
(Ⅲ)若点A在第一象限,证明:当k>0时,恒有![]() >
>![]() .
.
20.本小题主要考查平面向量,椭圆的定义、标准方程及直线与椭圆位置关系等基础知识,考查综合运用解析几何知识解决问题的能力.满分12分.
解:(Ⅰ)设P(x,y),由椭圆定义可知,点P的轨迹C是以![]() 为焦点,长半轴为2的椭圆.它的短半轴
为焦点,长半轴为2的椭圆.它的短半轴![]() ,
,
故曲线C的方程为![]() .···················································································· 3分
.···················································································· 3分
(Ⅱ)设![]() ,其坐标满足
,其坐标满足
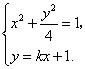
消去y并整理得![]() ,
,
故![]() .······································································· 5分
.······································································· 5分
若![]() ,即
,即![]() .
.
而![]() ,
,
于是![]() ,
,
化简得![]() ,所以
,所以![]() .············································································ 8分
.············································································ 8分
(Ⅲ)![]()
![]()
![]()
![]() .
.
因为A在第一象限,故![]() .由
.由![]() 知
知![]() ,从而
,从而![]() .又
.又![]() ,
,
故![]() ,
,
即在题设条件下,恒有![]() .
.
22.(本小题满分14分)
已知函数![]() (
(![]() ),其中
),其中![]() .
.
(Ⅰ)当![]() 时,讨论函数
时,讨论函数![]() 的单调性;
的单调性;
(Ⅱ)若函数![]() 仅在
仅在![]() 处有极值,求
处有极值,求![]() 的取值范围;
的取值范围;
(Ⅲ)若对于任意的![]() ,不等式
,不等式![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的取值范围.
的取值范围.
本小题主要考查利用导数研究函数的单调性、函数的最大值、解不等式等基础知识,考查综合分析和解决问题的能力.满分14分.
(Ⅰ)解:![]() .
.
当![]() 时,
时,![]() .
.
令![]() ,解得
,解得![]() ,
,![]() ,
,![]() .
.
当![]() 变化时,
变化时,![]() ,
,![]() 的变化情况如下表:
的变化情况如下表:
|
|
| 0 |
|
|
| 2 |
|
|
| - | 0 | + | 0 | - | 0 | + |
|
| ↘ | 极小值 | ↗ | 极大值 | ↘ | 极小值 | ↗ |
所以![]() 在
在![]() ,
,![]() 内是增函数,在
内是增函数,在![]() ,
,![]() 内是减函数.
内是减函数.
(Ⅱ)解:![]() ,显然
,显然![]() 不是方程
不是方程![]() 的根.
的根.
为使![]() 仅在
仅在![]() 处有极值,必须
处有极值,必须![]() 成立,即有
成立,即有![]() .
.
解些不等式,得![]() .这时,
.这时,![]() 是唯一极值.
是唯一极值.
因此满足条件的![]() 的取值范围是
的取值范围是![]() .
.
(Ⅲ)解:由条件![]() ,可知
,可知![]() ,从而
,从而![]() 恒成立.
恒成立.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
因此函数![]() 在
在![]() 上的最大值是
上的最大值是![]() 与
与![]() 两者中的较大者.
两者中的较大者.
为使对任意的![]() ,不等式
,不等式![]() 在
在![]() 上恒成立,当且仅当
上恒成立,当且仅当![]() ,即
,即![]() ,在
,在![]() 上恒成立.
上恒成立.
所以![]() ,因此满足条件的
,因此满足条件的![]() 的取值范围是
的取值范围是![]() .
.