高二理科数学下学期调研试题（）
(考试时间：120分钟 满分：150分)
第Ⅰ卷（选择题 共40分）
一.选择题：（本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的. 请把答案填在答题卡上）
1．
,
,
( )
A.
B. 
C.
D. 
2. 已知
A.
B. 
C. 
D.
3．如图，甲、乙、丙是三个立方体图形的三视图，甲、乙、丙对应的标号正确的是（ ）.
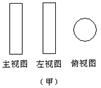
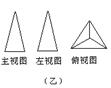
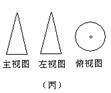
①长方体 ②圆锥 ③三棱锥 ④圆柱
A．④③② B． ②①③ C． ①②③ D． ③②④
4．给出下列函数①
，②
③
④
其中是偶函数的有（
）.
A．1个 B．2个 C．3 个 D．4个
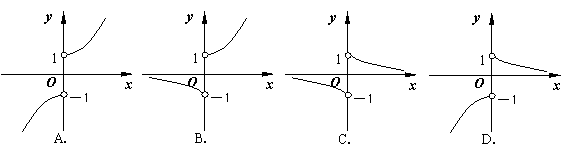5. 函数
的图象的大致形状是（ ）.
6．甲、乙两人下棋，甲获胜的概率是40%，甲不输的概率为90%，则甲、乙二人下成和棋的概率为（ ）.
A．60% B．30%
C．10% D．50%
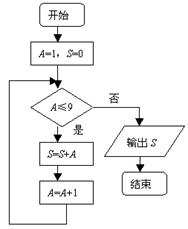
7．如图，该程序运行后输出的结果为（ ）.
A．36 B．
8. 已知平面向量
，且
∥ 
，则实数
的值等于（ ）.
A．
或
B．
C．
或 D．
二．填空题:（每题6分共30分）
9. 
10. 
11. 已知
12. 
13. 
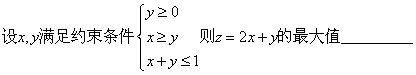
14.设
，
，
是空间的三条直线，下面给出四个命题：
①若
，
，则
；
②若、是异面直线，、是异面直线，则、也是异面直线；
③若和相交，和相交，则和也相交；
④若和共面，和共面，则和也共面．
其中真命题的个数是________个.
高二理科数学下学期调研试题
一、选择题答题卡（5
8=40）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 |
二、填空题（56=30）
9． 10． 11． 12．
13.___________ 14．
三、解答题：(本大题6小题，共80分.解答应写出文字说明、证明过程或演算步骤)
15．(本小题满分12分) 已知
．
16. (本小题满分12分)已知等差数列
,
(1)求的通项公式；(2) 
哪一个最大？并求出最大值
17．(本小题满分14分)
已知圆C 
，
切点为A，B（1）求直线PA,PB的方程 （2）求过P点的圆的切线长
18 (本小题满分14分)
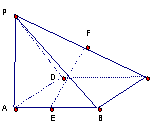
如图，在四棱锥P-ABCD中，底面ABCD是矩形，侧棱PA⊥底面ABCD，E,F分别是AB,PC的中点F．
（1）证明 CD⊥PD；（2）证明EF//平面PAD .
 | |||
| |||
19．(本小题满分14分)
某家庭用14.4万购买一辆汽车，使用中维修费用逐年上升。第n年维修的费用为0.2n万元，每年其他的费用为0.9万元。报废损失最小指的是购车费，维修费及其他费用之和的年平均值最小，则这辆车应在多少年后报废损失最小？
20．(本小题满分14分)
已知定义在
成立，且当x>1时，
（1）求f
(1)的值 （2）证明：f (x)在
.
高二数学调研试题（理科）
参 考 答 案
一.选择题：DAABDDDC
二．填空题:
9. 
10. 156 11. 15 12. 
13
.2 14. 0
三、解答题：
15．
--------------------------------------------------------------------------------5分
(2) 
----------------------------------------------------------------------12分
16.解：（1）由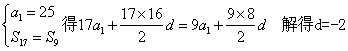
--------------------------6分
（2）
---------------------------------------12分
17.解：
-------------------------8分
---------------------------------------------------14分
18. 证明：
--------------------------------------7分
E,F分别是AB,PC的中点，
∴FN∥PD，EN∥AD
∴FN∥平面PAD，EN∥平面PAD
又∵
∴平面 ENF∥平面PAD
，∴EF∥平面PAD .--------------------------------14分
19．解：由题意可得，年平均值
当且仅当
-------------------------------------------------14分
20．解：（1）令x=y=1,得f (1)= f 1）+ f (1)
所以f (1)=0--------------------------------------------------------------5分
(2)设
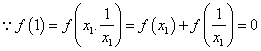
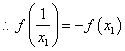
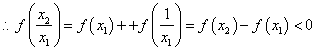
----------------------14分
以上各题如有其他解法，请评卷老师酌情给分.