高二理科数学第一学期抽考考试
高二(理科)数学试题
本试卷共150分,120分钟完成,答案写在答题卷上。
第Ⅰ卷
一、 选择题 (本大题共8小题,每小题5分,共40分)
1. 设函数![]() 的定义域为集合M,集合N=
的定义域为集合M,集合N=![]() ,则
,则![]() ( ).
( ).
A.![]() B.N C.
B.N C.![]() D.M
D.M
2.若![]() (i为虚数单位),则使
(i为虚数单位),则使![]() 的
的![]() 值可能是( )
值可能是( )
A.0 B.![]() C.
C.![]() D.
D.![]()
3.已知![]() 成等比数列,且曲线
成等比数列,且曲线![]() 的顶点是
的顶点是![]() ,则
,则![]() 等于( )
等于( )
A.3 B.![]()
4. 设向量![]() 与
与![]() 的夹角为
的夹角为![]() ,
,![]() =(2,1),3
=(2,1),3![]() +
+![]() =(5,4),则
=(5,4),则![]() = ( )
= ( )
![]() .
.![]()
![]() .
. ![]()
![]() .
.![]()
![]() .
.![]()
5.函数![]() (其中
(其中![]() 为自然对数的底数)的零点所在的区间是( )
为自然对数的底数)的零点所在的区间是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
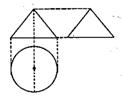 6.如右图,一个空间几何体的主视图和左视图都是边长为1的正三角形,俯视图是一个圆,
6.如右图,一个空间几何体的主视图和左视图都是边长为1的正三角形,俯视图是一个圆,
那么几何体的侧面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
7.奇函数![]() 在
在![]() 上是减函数,常数
上是减函数,常数![]() 满足
满足![]() 且
且![]() ,则下列式子正确的是( )
,则下列式子正确的是( )
![]()
![]()
![]() D、
D、![]()
8.过双曲线一焦点且垂直于双曲线实轴的直线交双曲线于A、B两点,若以AB为直径的
圆恰过双曲线的一个顶点,则双曲线的离心率是( )
A.![]() B.
B.![]() D.2
D.2
 第Ⅱ卷
第Ⅱ卷
二、填空题(每小题5分,满分30分.)
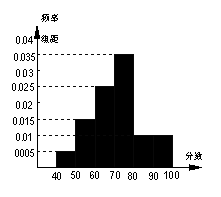
9.统计某校1000名学生的数学会考成绩,得到样
本频率分布直方图如右图示,规定不低于60分为
及格,不低于80分为优秀,则及格人数是 ;
优秀率为 。
10.函数![]() 的定义域是 。
的定义域是 。
11.计算定积分![]() 。
。
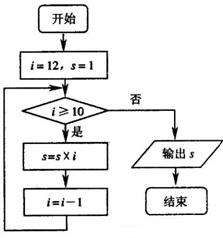
12.下面框图表示的程序所输出的结果是 。
13. 已知![]() 是定义在
是定义在![]() 上的函数,且对任意
上的函数,且对任意![]() ,都有:
,都有:![]() ,又
,又![]() 则
则![]() 。
。
14. 若实数![]() 满足条件
满足条件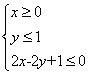 ,则目标函数
,则目标函数![]() 的最大值为 。
的最大值为 。
三、解答题:(本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.)
15.(本小题满分12分)
在△ABC中,![]() 、
、![]() 、
、![]() 是角
是角![]() 所对的边,且满足
所对的边,且满足![]() .
.
(Ⅰ)求角![]() 的大小;
的大小;
(Ⅱ)设![]() ,求
,求![]() 的最小值.
的最小值.
16.(本小题满分14分)
一个盒子中装有标号为0,1,2,3,4,5的6张标签,随机地选取两张标签。
(Ⅰ) 求选出的两张标签的数字之和为5的概率;
(Ⅱ)如果用选出的两张标签的数字能组成一个两位数,求这个两位数能被5整除的概率。
 17.(本小题满分14分)
17.(本小题满分14分)
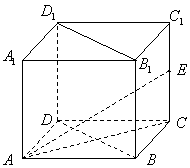
已知:正方体![]() ,
,![]() ,
,![]() 为棱
为棱![]() 的中点.
的中点.
(Ⅰ) 求证:![]() ;
;
(Ⅱ) 求证:![]() 平面
平面![]() ;
;
(Ⅲ)求三棱锥![]() 的体积.
的体积.
18.(本小题满分14分)
设函数![]() (a、b、c、d∈R)满足:
(a、b、c、d∈R)满足:![]() 都有
都有![]() ,且x=1时,
,且x=1时,![]() 取极小值
取极小值![]()
(Ⅰ)![]() 的解析式;
的解析式;
(Ⅱ)当![]() 时,证明:函数图象上任意两点处的切线不可能互相垂直;
时,证明:函数图象上任意两点处的切线不可能互相垂直;
19.(本小题满分14分)
|
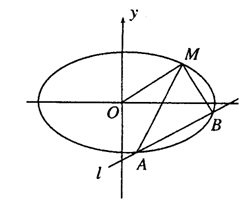
(Ⅰ)求椭圆的方程;
(Ⅱ)求![]() 的取值范围,
的取值范围,
(Ⅲ)求证直线![]() 、
、![]() 与
与![]() 轴始终围成一个等腰三角形.
轴始终围成一个等腰三角形.
20. (本题满分12分)
已知数列![]() 的前
的前![]() 项和
项和![]() 和通项
和通项![]() 满足
满足![]() 。
。
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ) 求证:![]() ;
;
(Ⅲ)设函数![]() ,
,![]() ,求
,求![]() .
.
高二(理科)数学试题参考答案
一、 选择题(5’×8=40’)
DBBDB ABD
二、填空题(5’×6=30’)
9、800 20% 10、![]() 11、
11、![]() 12、1320 13、
12、1320 13、![]() 14、2
14、2
三、解答题:
15. 解:(Ⅰ)∵![]() ,∴
,∴![]() , ………………3分
, ………………3分
又∵![]() ,∴
,∴![]() . ……………………………………………5分
. ……………………………………………5分
(Ⅱ)![]() ……………………………………………6分
……………………………………………6分
![]() , ………………………8分
, ………………………8分
∵![]() ,∴
,∴![]() . ……………10分
. ……………10分
∴当![]() 时,取得最小值为
时,取得最小值为![]() . …………12分
. …………12分
16、解:(1)求两张标签数字之和的基本事件有:0-1.,0-2,0-3,0-4,0-5,1-2,1-3,1-4,1-5,2-3,2-4,2-5,3-4,3-5,4-5,共15种, (2分)
数字之和为5的基本事件有:0-5,1-4,2-3,共3种,(4分)
每个基本事件出现的概率相等.(5分)
所以: ![]()
![]() (6分)
(6分)
(2)任取两张标签能组成的两位数共有:十位是1的有:5个;十位是2的有:5个
十位是3的有:5个;十位是4的有:5个;十位是5的有:5个;总共25个。(8分)
能被5整除的有:个位是0的5个,个位是5的有4个总共9个, (9分)
每一个两位数出现的概率相等。 (10分)
所以: ![]() (11分)
(11分)
答:选出的两张标签的数字之和为5的概率是![]() ,这个两位数能被5整除的概率是
,这个两位数能被5整除的概率是![]() 。
。
(12分)
17.解:(Ⅰ)证明:连结![]() ,则
,则![]() //
//![]() , …………1分
, …………1分
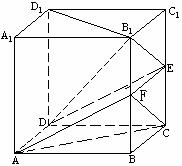 ∵
∵![]() 是正方形,∴
是正方形,∴![]() .∵
.∵![]() 面
面![]() ,∴
,∴![]() .
.
又![]() ,∴
,∴![]() 面
面![]() . ………………4分
. ………………4分
∵![]() 面
面![]() ,∴
,∴![]() ,
,
∴![]() . …………………………………………5分
. …………………………………………5分
(Ⅱ)证明:作![]() 的中点F,连结
的中点F,连结![]() .
.
∵![]() 是
是![]() 的中点,∴
的中点,∴![]()
![]()
![]() ,
,
∴四边形![]() 是平行四边形,∴
是平行四边形,∴ ![]() . ………7分
. ………7分
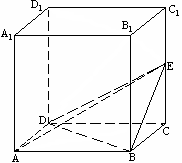 ∵
∵![]() 是
是![]() 的中点,∴
的中点,∴![]() ,
,
又![]() ,∴
,∴![]() .
.
∴四边形![]() 是平行四边形,
是平行四边形,![]() //
//![]() ,
,
∵![]() ,
,![]() ,
,
∴平面![]() 面
面![]() . …………………………………9分
. …………………………………9分
又![]() 平面
平面![]() ,∴
,∴![]() 面
面![]() . ………………10分
. ………………10分
(3)![]() . ……………………………11分
. ……………………………11分
![]() . ……………………………14分
. ……………………………14分
18、解:(I)因为,![]() 成立,所以:
成立,所以:![]() ,
,
由:![]() ,得
,得 ![]() ,
,
由:![]() ,得
,得 ![]()
解之得:![]() 从而,函数解析式为:
从而,函数解析式为:![]() …………7分
…………7分
(2)由于,![]() ,设:任意两数
,设:任意两数 ![]() 是函数
是函数![]() 图像上两点的横坐标,则这
图像上两点的横坐标,则这
两点的切线的斜率分别是:![]() …………9分
…………9分
又因为:![]() ,所以,
,所以,![]() ,得:
,得:![]() ………12分
………12分
知: ![]() ………………………………………………………………………13分
………………………………………………………………………13分
故,当![]() 是函数
是函数![]() 图像上任意两点的切线不可能垂直…………………14分
图像上任意两点的切线不可能垂直…………………14分
19、解:(1)设椭圆方程为![]() ………………………1分
………………………1分
则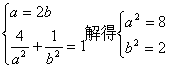 ………………………………………………3分
………………………………………………3分
∴椭圆方程为![]() …………………………………………………………4分
…………………………………………………………4分
(2)∵直线l平行于![]() ,且在
,且在![]() 轴上的截距为
轴上的截距为![]() ,又
,又![]()
![]() ……………………………………………………5分
……………………………………………………5分
由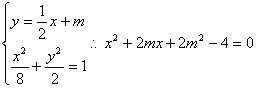 ……………………………………6分
……………………………………6分
∵直线l与椭圆交于A、B两个不同点,
![]()
(3)设直线MA、MB的斜率分别为k1,k2,只需证明k1+k2=0即可…………9分
设![]() ……………………10分
……………………10分
则![]()
由![]()
![]() ……………………………………………………10分
……………………………………………………10分
而![]()
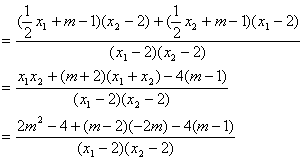
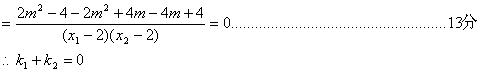
故直线MA、MB与x轴始终围成一个等腰三角形.……………………14分
20.解:(Ⅰ)当![]() 时
时
![]() ,
,![]()
∴![]() ,---------------------4分
,---------------------4分
由![]()
![]() 得
得![]()
∴数列![]() 是首项
是首项![]() 、公比为
、公比为![]() 的等比数列,∴
的等比数列,∴![]() ----6分
----6分
(Ⅱ)证法1: 由![]() 得
得![]()
![]() --------------------8分
--------------------8分
![]() ,∴
,∴![]()
∴![]() -------------------------10分
-------------------------10分
〔证法2:由(Ⅰ)知![]() ,
,
∴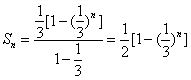 --------------------------------8分
--------------------------------8分
![]() ,∴
,∴![]() --------------------9分
--------------------9分
即![]() --------------------------------10分〕
--------------------------------10分〕
(Ⅲ) ![]()
![]() =
=![]()
=![]() -------------------12分
-------------------12分
∵![]()
∴![]()
![]()
![]() =
=![]() -----14分
-----14分