高二理科数学第二学期期末调研试卷
高二数学(理科)
本试卷共4页,20小题,满分150分.考试用时120分钟.
注意事项:
1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自已的姓名、班别、学号、试室号填写在答题卡上.
2.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上.
参考公式及数据:
用最小二乘法求线性回归方程系数公式 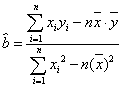 ,
,![]() .
.
随机变量![]() 的临界值表:
的临界值表:
|
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
|
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
一、选择题:本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.若![]() ,其中
,其中![]() ,
,![]() 是虚数单位,则
是虚数单位,则![]() ( )
( )
A.![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
2.下列推理过程是类比推理的为( )
A. 人们通过大量试验得出抛硬币出现正面的概率为0.5;
B. 鲁班通过研究带齿的草叶和蝗虫的齿牙,发明了锯;
C. 通过检验溶液的PH值得出溶液的酸碱性;
D. 数学中由周期函数的定义判断某函数是否为周期函数.
3.通过残差来判断模型拟合的效果,判断原始数据中是否存在可疑数据,这方面的分析工作称为残差分析,那么残差图中的残差点比较均匀地落在较窄的水平的带状区域中,说明( )
A. 模型选用得不合适,模型拟合精度不高,从而得出回归方程的预报精度不高。
B. 模型选用得比较合适,模型拟合精度较高,从而得出回归方程的预报精度较高。
C. 模型选用得合适,模型拟合精度较高,但回归方程的预报精度不高。
D. 模型选用得合适,但模型拟合精度不高,从而得出回归方程的预报精度不高。
4.一工厂生产的100个产品中有90个一等品,10个二等品,现从这批产品中抽取4个,则其中恰好有一个二等品的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
5.已知随机变量![]() ,且
,且![]() ,
,![]() ,则
,则![]() 与
与![]() 的值分别为 ( )
的值分别为 ( )
A.16与0.8 B.20与
6.设随机变量![]() 服从标准正态分布
服从标准正态分布![]() ,在某项测量中,已知
,在某项测量中,已知![]() 在
在![]() 内取值的概率为0.025,则
内取值的概率为0.025,则![]() =( )
=( )
A.0.025 B.
7. 在5道题中有3道理科题和2道文科题.不放回地依次抽取2道题,则在第1次抽到理科题的条件下,第2次抽到理科题的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.定义![]() 的运算分别对应下图中的(1)、(2)、(3)、(4),那么下图中的(A)、(B)所对应的运算结果可能是( )
的运算分别对应下图中的(1)、(2)、(3)、(4),那么下图中的(A)、(B)所对应的运算结果可能是( )
 |
(1) (2) (3) (4) (A) (B)
A. ![]() B.
B.![]() C.
C. ![]() D.
D.![]()
二、填空题:本大题共6小题,每题5分,共30分.
9.已知集合A=![]() ,那么A的所有子集的个数是
。
,那么A的所有子集的个数是
。
10.根据定积分的几何意义,计算![]() __。
__。
11.通过计算高中生的性别与喜欢数学课程列联表中的数据,得到![]() ,那么可以得
,那么可以得
到结论: 约有 的把握认为性别与喜欢数学之间有关系。
12.一射手对同一目标独立地射击四次,已知至少命中一次的概率为![]() ,则此射手每次射击命中的概率为 。
,则此射手每次射击命中的概率为 。
|
|
|
|
|
|
|
|
|
|
13.设![]() 是一个离散型随机变量,其分布列如下:
是一个离散型随机变量,其分布列如下:
则![]() =
。
=
。
14.由等式![]()
![]()
定义映射![]() 。
。
三、解答题:本大题共6小题,共80分,解答应写出文字说明、证明过程或演算步骤.
 15.(本小题满分12分)
15.(本小题满分12分)
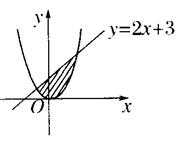
如图,求直线![]() 与抛物线
与抛物线![]() 所围成图形的面积.
所围成图形的面积.
16.(本小题满分12分)
某种产品的广告费支出x与销售额y(单位:百万元)之间有如下的对应数据:
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 50 | 60 | 70 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() =
=![]() x+
x+![]() ;
;
(3)要使这种产品的销售额突破一亿元(含一亿元),则广告费支出至少为多少百万元?
(结果精确到0.1,参考数据:2×30+4×40+5×50+6×60+8×70=1390)。
17.(本小题满分14分)
在二项式![]() 的展开式中,
的展开式中,
(1)若所有二项式系数之和为![]() ,求展开式中二项式系数最大的项.
,求展开式中二项式系数最大的项.
(2)若前三项系数的绝对值成等差数列,求展开式中各项的系数和。
18.(本小题满分14分)
已知函数![]() ,
,
(1)求![]() 的单调区间;
的单调区间;
(2)求![]() 在
在![]() 上的最大值和最小值。
上的最大值和最小值。
19.(本小题满分14分)
某电视台举行电视奥运知识大奖赛,比赛分初赛和决赛两部分.为了增加节目的趣味性,
初赛采用选手选一题答一题的方式进行,每位选手最多有![]() 次选题答题的机会,选手累计答对
次选题答题的机会,选手累计答对![]() 题或答错
题或答错![]() 题即终止其初赛的比赛,答对
题即终止其初赛的比赛,答对![]() 题者直接进入决赛,答错
题者直接进入决赛,答错![]() 题者则被淘汰.已知选手甲答题的正确率为
题者则被淘汰.已知选手甲答题的正确率为![]() .
.
(1) 求选手甲可进入决赛的概率;
(2) 设选手甲在初赛中答题的个数为![]() ,试写出
,试写出![]() 的分布列,并求
的分布列,并求![]() 的数学期望.
的数学期望.
20.(本小题满分![]() 分)
分)
设![]() 是由非负整数组成的数列,且满足
是由非负整数组成的数列,且满足![]() ,
,![]() ,
,
![]() ,
,![]()
(1)求![]() ;
;
(2)证明![]() ,
,![]()
(3)求![]() 的通项公式。
的通项公式。
附加题(本题为附加题,如果解答正确,加5 分,但全卷总分不超过150分)
若存在实常数![]() 和
和![]() ,使得函数
,使得函数![]() 和
和![]() 对其定义域上的任意实数
对其定义域上的任意实数![]() 分别满足:
分别满足:![]() 和
和![]() ,则称直线
,则称直线![]() 为
为![]() 和
和![]() 的“隔离直线”.
的“隔离直线”.
已知![]() ,
,![]() 为自然对数的底数).问:
为自然对数的底数).问:
函数![]() 和
和![]() 是否存在“隔离直线”?若存在,求出此隔离直线方程;若不存在,请说明理由.
是否存在“隔离直线”?若存在,求出此隔离直线方程;若不存在,请说明理由.