立体几何(三) 孙还海
一. 选择题
1.平行六面体ABCD-A1B
A 重心 B 外心 C 内心 D 垂心
2.长方体三条棱分别为a,b,c, 若长方体所有的棱长度之和为24,一条对角线为5,体积为2,则![]() 等于
( )
等于
( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
3.已知,正四棱锥侧面是正三角形,设侧面与底面所成的二面角为![]() ,相邻两侧面所成的二面角为
,相邻两侧面所成的二面角为![]() ,则 (
)
,则 (
)
A ![]() B
B ![]() C
C ![]() D
D ![]()
4.在北纬450圈上,有甲、已两地。它们的经度分别为东经1400和西经1300,地球的半径是R,则甲、已两地球面距离是 ( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
5.某简单多面体每个面都是三角形,经过每个顶点有四条棱,则该多面体的面数为( )
A 6 B
二.填空题
6.三棱锥的三条侧棱两两垂直,底面上一点到三个侧面的距离分别是2,3,6,则这个点到三棱锥顶点的距离是____________________
7.半径为5的球被两个平行平面所截,两截面圆的半径分别是3,4,则两截面间距离为____________
8.一个三棱锥的三个侧面中有两个是等腰直角三角形,另一个是边长为1的正三角形,这样的三棱锥的体积为_________________(写出一个可能的值)。
9.正三棱锥的侧棱与底面所成的角的正切值为![]() ,则棱锥的侧面积与全面积之比为______________
,则棱锥的侧面积与全面积之比为______________
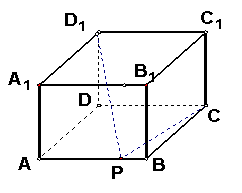 10.已知长方体ABCD-A1B
10.已知长方体ABCD-A1B![]() ,则棱AD的长的取值范围是______
,则棱AD的长的取值范围是______
三.解答题。
 11.在四面体ABCD中,
11.在四面体ABCD中,![]() 。
。
(1)求证: ![]()
(2)是否存在这样的四面体,使二面角C-AD-B的平面角为300 ?如果存在,求出CD的长;如果不存在,请找出一个角![]() ,使得存在这样的四面体,使二面角C-AD-B的平面角为
,使得存在这样的四面体,使二面角C-AD-B的平面角为![]() 。
。

12.如图,三棱锥P-ABC中侧面PAC^底面ABC;PA=BC=a
,PC=AB=
求证(1)PA^面ABC
(2)求二面角P-BD-A的正切值 ;
(3)求点A到平面PBD的距离
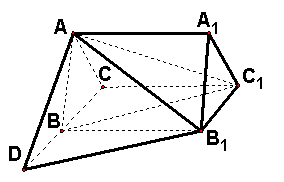
13.如图,正三棱柱ABC-A1B![]() ,D是CB延长线上一点,且BD=BC,
,D是CB延长线上一点,且BD=BC,
(1)求证:直线BC1‖平面AB1D ;
(2)求二面角B1-AD-B的大小;
(3)求三棱锥C1-ABB1的体积。、