立体几何（1）

一．选择题：

1．空间五点A,B,C,D,E不共面，已知A,B,C,D在同一个平面内，点B,C,D,E在同一个平面内，那么B,C,D三点(　　)

A. 一定构成三角形　　 　 B.一定共线　　　　C. 不一定共线　　　 D.与A,E共面

2．空间四点中，如果其中任意三点都不共线，那么经过其中三点的平面(　　)

A.必定有4个  B.要么4个，要么1只有个　C. 要么3个，要么1只有个 　D.1,3,4都可能

3. 在长方体AC₁的12条面对角线中，有多少对异面直线(　　)

A. 30　　 　　　B.60  　　　　　C.24　　 　　　　　D.48

4.棱长为a的正方体中，连结相邻面的中心，以这些线段为棱的八面体的体积为（　　）

A.　　　　　 B. 　　　　 C.  　　　　　　D.

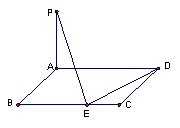
5．已知矩形ABCD（如图）中,AB=3,BC=a,若PA⊥平面AC，在BC边上去一点E, 使PE⊥DE，则满足条件的E点有两个时，a的取值范围是(　　)

A.a>6 　　　　　B.a≥6 　　　C. 0<a<6　　　  D. 0<a≤6

二．填空题：

6． a,b是两直线，α,β是两平面，且a⊥α,b⊥β,a，b，则当______________时，有α⊥β（填一种条件即可）

7．如图为正方体的平面展开图，在这个正方体中

①BM与ED平行　　  ②CN与BE是异面直线

③CN与BM成60⁰角　④DM与BN垂直，

其中正确命题序号是______________________

8．对于四面体ABCD，给出下列四个命题：

①若AB=AC,BD=CD则BC⊥AD 　 ②若AC=CD,AC=BD则BC⊥AD

③若AB⊥AC,BD⊥CD则BC⊥AD　④若AB⊥CD,BD⊥AC则BC⊥AD

其中真命题的序号是_______________________

9．正四棱锥P-ABCD中，异面直线PA,BC所成角的取值范围是__________________

10．在一个45^o的二面角的一个半平面内有一条直线与二面角棱成45^o，则此直线与二面角的另一个面所成角为__________________

三．解答题：

11．已知三个平面α,β,两两相交，a,b,c是三条交线，若a∩b=P

求证：a,b,c交于一点

12．四棱锥P-ABCD的底面是矩形，侧面PAD是正三角形且侧面PAD⊥面ABCD，

当的值是多少时，能使PB⊥AC?并证明.

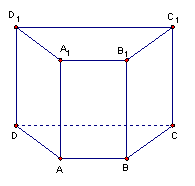13．如图,直四棱柱ABCD- A₁B₁C₁D₁的底面是梯形,AB∥CD,AD⊥DC,CD=2,DD₁=AB=1,P,Q分别是CC₁,C₁D₁的中点.点P到直线AD₁的距离为

①求证:AC∥面BPQ

②求二面角B-PQ-D的大小