立体几何（4）

一．选择题：

1．一个四面体的所有棱长都是，四个顶点在同一球面上，则此球的表面积为(　　)

A.3π　　 　　 B.4π　　　　C. π　　　 D.6π

2．正方体ABCD- A₁B₁C₁D₁ 中，E,F分别是正方形ADD₁A₁和ABCD的中心，G是CC₁的中点，设GF, C₁E与AB所成的角分别为α,β，则α+β等于(　　)

A. 120⁰ 　　　 B. 90⁰ 　　　C. 75⁰ 　　　　 D. 60⁰

3. 三个平α,β,面两两垂直，它们的三条交线交于一点O，点P到这三个平面的距离之比为1:2:3且OP=，则点P到这三个平面的距离分别是(　　)

A. 2,4,6　　　　　B.3,6,9 　　　　　C.4,8,12　　 　　　　　D.5,10,15

4.已知球的表面积为20π,球面上有A,B,C三点,如果AB=AC=2,BC=,则球心到平面ABC的距离为（　　）

A.  1　　　　B. 　　　　C.  　　　　　　D. 2

5．AB,CD 是一对异面直线,E,F分别是AB,CD中点,M是BC中点，则(　　)

A.2EF>AC+BD 　　　　　B. 2EF=AC+BD　　　 C. 2EF<AC+BD　　　  D. 无法确定

二．填空题：

6．正方体ABCD- A₁B₁C₁D₁ 的12条棱中，互相垂直的棱共有___________条

7．正三棱锥的底面边长为a，侧棱长为l，则的范围是___________________

8．在四面体ABCD中，AB=CD=2,且AB,CD所成角为60⁰，E,F分别为BC,AD中点，则EF长为_______________

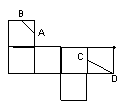
9．如图，是一个正方体的展开图，A,B,C均为棱的中点，D是顶点，则在正方体中异面直线AB和CD的夹角余弦值为__________________

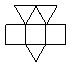
10．如图，是一个凸多面体的侧面展开图，则该多面体共有___________顶点

三．解答题：

11．已知正四棱柱ABCD- A₁B₁C₁D₁,AB=1,AA₁=2,点E为CC₁中点, 点F为BD₁中点.

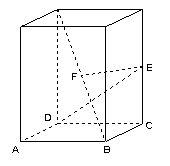（1）求证：EF为BD₁与CC₁的公垂线

（2）求点D₁到面BDE的距离

12．正方形ABCD,ABEF的边长都是1，而且平面ABCD,ABEF互相垂直，点M在AC上移动，点N在BF上移动，若CM=BN=a

（1）求MN的长

（2）当a为何值时，MN的长最小

（3）当MN长最小时，求面MNA与面MNB所成的二面角的大小

13．已知四个面都是直角三角形的三棱锥，其中三个面展开后构成一直角梯形ABCD,如图AD⊥AB，AD⊥DC,AB=2a,BC=,CD=a

（1）请设计一种虚线，沿虚线翻折成原来的三棱锥（指三棱锥的三个面）

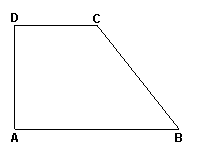（2）求这个三棱锥外接球的体积