解析几何（三）　主备：黄万荣

一．选择题

1．若不论k为何值，直线y=k(x-2)+b,与曲线x²-y²=1,总有 公共点，则b的取值范围是（ ）

 A 　　　B　　　 C （-2 ，2）　　　D [-2 ，2]

2．F_{1 ，}F₂是双曲线的两个焦点。Q是双曲线上任一点，从某一焦点引Ð F₁ QF₂平分线的垂线，垂足为P，则P点的轨迹是　　　　　　　　　　　　　　　　　  　　　（　　　）

A 直线　　　　　 B　圆　　　　　  C　椭圆　　　　　 D 双曲线

3．若x²+4y²=4 ,则 f(x,y)=x²+2xy+4y²+x+2y的最大值为　　　　　　　　　　  （　　 ）

A 　　　B 　　　 C 　　　　D
4。设F₁ ，F₂是双曲线的两个焦点,点P在双曲线上,且,则的值等于　　　　　　　　　　　　　　　　　　　　　　　　　  (　　　)

A　2　　　　　　  B 　　　　　C　4　　　　　　 D　18

5.已知对称轴为坐标轴的双曲线的两渐进线方程为，若双曲线上有一点M（x₀, y₀）,使，则双曲线的焦点　　 （　　 ）

A 在X轴上　　B 在Y轴上　　  C 当a>b时在X轴上　　 D 当a>b时在Y轴上

6．关于x的方程有解，则实数m的取值范围是________________

7B₁,B₂是椭圆短轴的两端点，过焦点F₁作长轴的垂线交椭圆于P，若是和的比例中项，则的值是_____________________________________________

8.设直线 ，抛物线 ，直线过点（2， 1）若直线与曲线C共有3个交点。则满足条件的直线的条数为_____________________________

9．椭圆　（）上一点P使 ，O为坐标原点，A为右顶点，则离心率e的范围是_______________________________________________

10．设双曲线 （a>0, b>0）中，离心率 ，则两条渐进线的夹角的取值范围是_______________________________

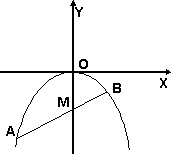11．已知：如图抛物线上有两点A（x₁,y₁）B(x₂ ,y₂),且

  1求证：　　　　 　　　　　　　　　 2若，求AB所在的直线方程。

12．从点M（-4，1）分别射向直线y=-2上两点P（x₁,y₁）和Q(x₂ ,y₂)，反射光线恰好通过椭圆C：　（）的两个焦点，已知椭圆的离心率为，且

1求椭圆的方程　　 2求入射光线MP所在的直线方程。

13．一动圆C位于Y轴的右方，且与定圆相外切且与Y轴相切，动圆圆心的轨迹为曲线E，点A，B在曲线上点M（a,0）， （其中为定值且满足）又平行，

　 1求a的范围　　　　2若线段AB的中垂线交X轴于N点，求RtDNAB的面积最大值。